Tuning Sequential Monte Carlo Samplers via Greedy Incremental Divergence Minimization

The performance of sequential Monte Carlo (SMC) samplers heavily depends on the tuning of the Markov kernels used in the path proposal. For SMC samplers with unadjusted Markov kernels, standard tuning objectives, such as the Metropolis-Hastings acceptance rate or the expected-squared jump distance, are no longer applicable. While stochastic gradient-based end-to-end optimization has been explored for tuning SMC samplers, they often incur excessive training costs, even for tuning just the kernel step sizes. In this work, we propose a general adaptation framework for tuning the Markov kernels in SMC samplers by minimizing the incremental Kullback-Leibler (KL) divergence between the proposal and target paths. For step size tuning, we provide a gradient- and tuning-free algorithm that is generally applicable for kernels such as Langevin Monte Carlo (LMC). We further demonstrate the utility of our approach by providing a tailored scheme for tuning \textit{kinetic} LMC used in SMC samplers. Our implementations are able to obtain a full \textit{schedule} of tuned parameters at the cost of a few vanilla SMC runs, which is a fraction of gradient-based approaches.

Personalized Convolutional Dictionary Learning of Physiological Time Series

Human physiological signals tend to exhibit both global and local structures: the former are shared across a population, while the latter reflect inter-individual variability. For instance, kinetic measurements of the gait cycle during locomotion present common characteristics, although idiosyncrasies may be observed due to biomechanical disposition or pathology. To better represent datasets with local-global structure, this work extends Convolutional Dictionary Learning (CDL), a popular method for learning interpretable representations, or dictionaries, of time-series data. In particular, we propose Personalized CDL (PerCDL), in which a local dictionary models local information as a personalized spatiotemporal transformation of a global dictionary. The transformation is learnable and can combine operations such as time warping and rotation. Formal computational and statistical guarantees for PerCDL are provided and its effectiveness on synthetic and real human locomotion data is demonstrated.

Covering Multiple Objectives with a Small Set of Solutions Using Bayesian Optimization

In multi-objective black-box optimization, the goal is typically to find solutions that optimize a set of T black-box objective functions, $f_1$, ..., $f_T$, simultaneously. Traditional approaches often seek a single Pareto-optimal set that balances trade-offs among all objectives. In this work, we introduce a novel problem setting that departs from this paradigm: finding a smaller set of K solutions, where K < T, that collectively "covers" the T objectives. A set of solutions is defined as "covering" if, for each objective $f_1$, ..., $f_T$, there is at least one good solution. A motivating example for this problem setting occurs in drug design. For example, we may have T pathogens and aim to identify a set of K < T antibiotics such that at least one antibiotic can be used to treat each pathogen. To address this problem, we propose Multi-Objective Coverage Bayesian Optimization (MOCOBO), a principled algorithm designed to efficiently find a covering set. We validate our approach through extensive experiments on challenging high-dimensional tasks, including applications in peptide and molecular design. Experiments demonstrate MOCOBO's ability to find high-performing covering sets of solutions. Additionally, we show that the small sets of K < T solutions found by MOCOBO can match or nearly match the performance of T individually optimized solutions for the same objectives. Our results highlight MOCOBO's potential to tackle complex multi-objective problems in domains where finding at least one high-performing solution for each objective is critical.

Fully Bayesian Wideband Direction-of-Arrival Estimation and Detection via RJMCMC

We propose a fully Bayesian approach to wideband, or broadband, direction-of-arrival (DoA) estimation and signal detection. Unlike previous works in wideband DoA estimation and detection, where the signals were modeled in the time-frequency domain, we directly model the time-domain representation and treat the non-causal part of the source signal as latent variables. Furthermore, our Bayesian model allows for closed-form marginalization of the latent source signals by leveraging conjugacy. To further speed up computation, we exploit the sparse ``stripe matrix structure'' of the considered system, which stems from the circulant matrix representation of linear time-invariant (LTI) systems. This drastically reduces the time complexity of computing the likelihood from $\mathcal{O}(N^3 k^3)$ to $\mathcal{O}(N k^3)$, where $N$ is the number of samples received by the array and $k$ is the number of sources. These computational improvements allow for efficient posterior inference through reversible jump Markov chain Monte Carlo (RJMCMC). We use the non-reversible extension of RJMCMC (NRJMCMC), which often achieves lower autocorrelation and faster convergence than the conventional reversible variant. Detection, estimation, and reconstruction of the latent source signals can then all be performed in a fully Bayesian manner through the samples drawn using NRJMCMC. We evaluate the detection performance of the procedure by comparing against generalized likelihood ratio testing (GLRT) and information criteria.

Approximation-Aware Bayesian Optimization

High-dimensional Bayesian optimization (BO) tasks such as molecular design often require 10,000 function evaluations before obtaining meaningful results. While methods like sparse variational Gaussian processes (SVGPs) reduce computational requirements in these settings, the underlying approximations result in suboptimal data acquisitions that slow the progress of optimization. In this paper we modify SVGPs to better align with the goals of BO: targeting informed data acquisition rather than global posterior fidelity. Using the framework of utility-calibrated variational inference, we unify GP approximation and data acquisition into a joint optimization problem, thereby ensuring optimal decisions under a limited computational budget. Our approach can be used with any decision-theoretic acquisition function and is compatible with trust region methods like TuRBO. We derive efficient joint objectives for the expected improvement and knowledge gradient acquisition functions in both the standard and batch BO settings. Our approach outperforms standard SVGPs on high-dimensional benchmark tasks in control and molecular design.

Demystifying SGD with Doubly Stochastic Gradients

Optimization objectives in the form of a sum of intractable expectations are rising in importance (e.g., diffusion models, variational autoencoders, and many more), a setting also known as "finite sum with infinite data." For these problems, a popular strategy is to employ SGD with doubly stochastic gradients (doubly SGD): the expectations are estimated using the gradient estimator of each component, while the sum is estimated by subsampling over these estimators. Despite its popularity, little is known about the convergence properties of doubly SGD, except under strong assumptions such as bounded variance. In this work, we establish the convergence of doubly SGD with independent minibatching and random reshuffling under general conditions, which encompasses dependent component gradient estimators. In particular, for dependent estimators, our analysis allows fined-grained analysis of the effect correlations. As a result, under a per-iteration computational budget of $b \times m$, where $b$ is the minibatch size and $m$ is the number of Monte Carlo samples, our analysis suggests where one should invest most of the budget in general. Furthermore, we prove that random reshuffling (RR) improves the complexity dependence on the subsampling noise.

Stochastic Approximation with Biased MCMC for Expectation Maximization

The expectation maximization (EM) algorithm is a widespread method for empirical Bayesian inference, but its expectation step (E-step) is often intractable. Employing a stochastic approximation scheme with Markov chain Monte Carlo (MCMC) can circumvent this issue, resulting in an algorithm known as MCMC-SAEM. While theoretical guarantees for MCMC-SAEM have previously been established, these results are restricted to the case where asymptotically unbiased MCMC algorithms are used. In practice, MCMC-SAEM is often run with asymptotically biased MCMC, for which the consequences are theoretically less understood. In this work, we fill this gap by analyzing the asymptotics and non-asymptotics of SAEM with biased MCMC steps, particularly the effect of bias. We also provide numerical experiments comparing the Metropolis-adjusted Langevin algorithm (MALA), which is asymptotically unbiased, and the unadjusted Langevin algorithm (ULA), which is asymptotically biased, on synthetic and real datasets. Experimental results show that ULA is more stable with respect to the choice of Langevin stepsize and can sometimes result in faster convergence.

Provably Scalable Black-Box Variational Inference with Structured Variational Families

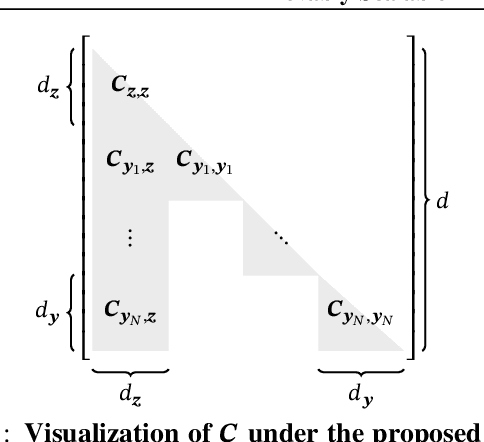
Variational families with full-rank covariance approximations are known not to work well in black-box variational inference (BBVI), both empirically and theoretically. In fact, recent computational complexity results for BBVI have established that full-rank variational families scale poorly with the dimensionality of the problem compared to e.g. mean field families. This is particularly critical to hierarchical Bayesian models with local variables; their dimensionality increases with the size of the datasets. Consequently, one gets an iteration complexity with an explicit $\mathcal{O}(N^2)$ dependence on the dataset size $N$. In this paper, we explore a theoretical middle ground between mean-field variational families and full-rank families: structured variational families. We rigorously prove that certain scale matrix structures can achieve a better iteration complexity of $\mathcal{O}(N)$, implying better scaling with respect to $N$. We empirically verify our theoretical results on large-scale hierarchical models.

Linear Convergence of Black-Box Variational Inference: Should We Stick the Landing?

We prove that black-box variational inference (BBVI) with control variates, particularly the sticking-the-landing (STL) estimator, converges at a geometric (traditionally called "linear") rate under perfect variational family specification. In particular, we prove a quadratic bound on the gradient variance of the STL estimator, one which encompasses misspecified variational families. Combined with previous works on the quadratic variance condition, this directly implies convergence of BBVI with the use of projected stochastic gradient descent. We also improve existing analysis on the regular closed-form entropy gradient estimators, which enables comparison against the STL estimator and provides explicit non-asymptotic complexity guarantees for both.

Black-Box Variational Inference Converges

We provide the first convergence guarantee for full black-box variational inference (BBVI), also known as Monte Carlo variational inference. While preliminary investigations worked on simplified versions of BBVI (e.g., bounded domain, bounded support, only optimizing for the scale, and such), our setup does not need any such algorithmic modifications. Our results hold for log-smooth posterior densities with and without strong log-concavity and the location-scale variational family. Also, our analysis reveals that certain algorithm design choices commonly employed in practice, particularly, nonlinear parameterizations of the scale of the variational approximation, can result in suboptimal convergence rates. Fortunately, running BBVI with proximal stochastic gradient descent fixes these limitations, and thus achieves the strongest known convergence rate guarantees. We evaluate this theoretical insight by comparing proximal SGD against other standard implementations of BBVI on large-scale Bayesian inference problems.