ASTRIDE: Adaptive Symbolization for Time Series Databases

We introduce ASTRIDE (Adaptive Symbolization for Time seRIes DatabasEs), a novel symbolic representation of time series, along with its accelerated variant FASTRIDE (Fast ASTRIDE). Unlike most symbolization procedures, ASTRIDE is adaptive during both the segmentation step by performing change-point detection and the quantization step by using quantiles. Instead of proceeding signal by signal, ASTRIDE builds a dictionary of symbols that is common to all signals in a data set. We also introduce D-GED (Dynamic General Edit Distance), a novel similarity measure on symbolic representations based on the general edit distance. We demonstrate the performance of the ASTRIDE and FASTRIDE representations compared to SAX (Symbolic Aggregate approXimation), 1d-SAX, SFA (Symbolic Fourier Approximation), and ABBA (Adaptive Brownian Bridge-based Aggregation) on reconstruction and, when applicable, on classification tasks. These algorithms are evaluated on 86 univariate equal-size data sets from the UCR Time Series Classification Archive. An open source GitHub repository called astride is made available to reproduce all the experiments in Python.

Extraction of Nystagmus Patterns from Eye-Tracker Data with Convolutional Sparse Coding

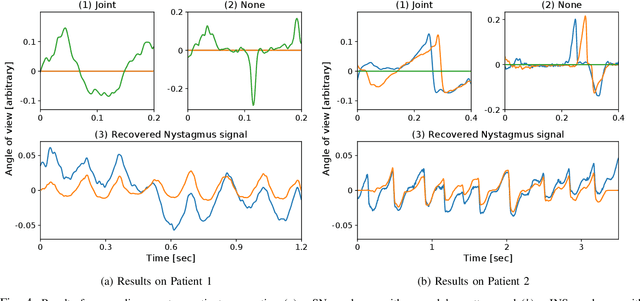
The analysis of the Nystagmus waveforms from eye-tracking records is crucial for the clinicial interpretation of this pathological movement. A major issue to automatize this analysis is the presence of natural eye movements and eye blink artefacts that are mixed with the signal of interest. We propose a method based on Convolutional Dictionary Learning that is able to automaticcaly highlight the Nystagmus waveforms, separating the natural motion from the pathological movements. We show on simulated signals that our method can indeed improve the pattern recovery rate and provide clinical examples to illustrate how this algorithm performs.

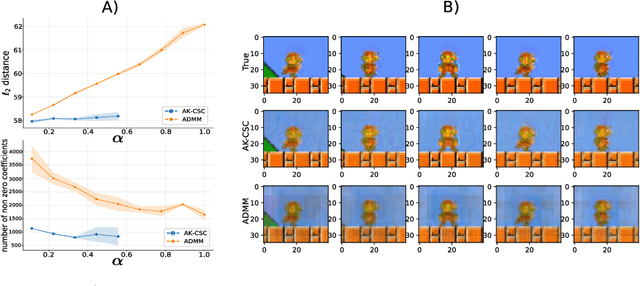
Tensor Convolutional Sparse Coding with Low-Rank activations, an application to EEG analysis

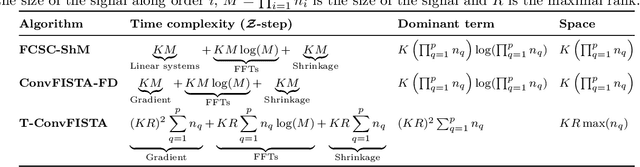
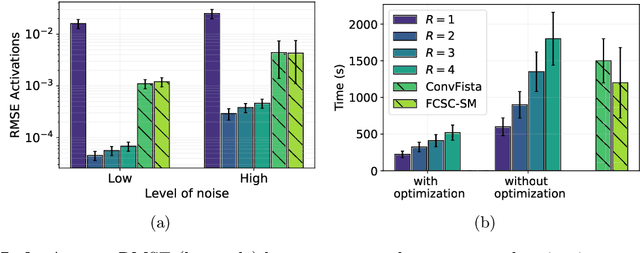
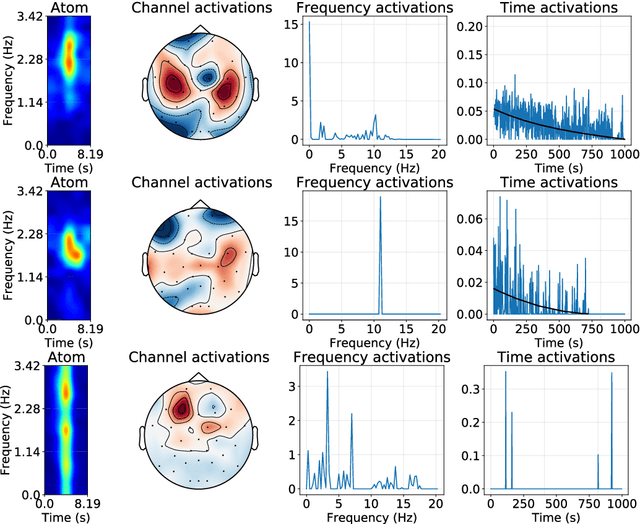
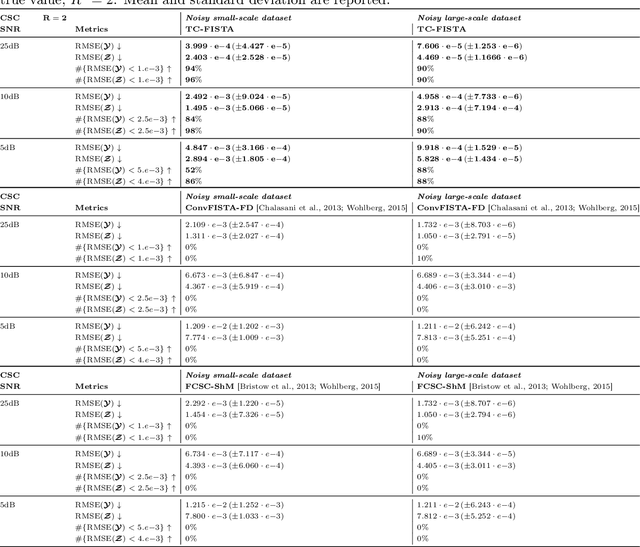
Recently, there has been growing interest in the analysis of spectrograms of ElectroEncephaloGram (EEG), particularly to study the neural correlates of (un)-consciousness during General Anesthesia (GA). Indeed, it has been shown that order three tensors (channels x frequencies x times) are a natural and useful representation of these signals. However this encoding entails significant difficulties, especially for convolutional sparse coding (CSC) as existing methods do not take advantage of the particularities of tensor representation, such as rank structures, and are vulnerable to the high level of noise and perturbations that are inherent to EEG during medical acts. To address this issue, in this paper we introduce a new CSC model, named Kruskal CSC (K-CSC), that uses the Kruskal decomposition of the activation tensors to leverage the intrinsic low rank nature of these representations in order to extract relevant and interpretable encodings. Our main contribution, TC-FISTA, uses multiple tools to efficiently solve the resulting optimization problem despite the increasing complexity induced by the tensor representation. We then evaluate TC-FISTA on both synthetic dataset and real EEG recorded during GA. The results show that TC-FISTA is robust to noise and perturbations, resulting in accurate, sparse and interpretable encoding of the signals.

Multivariate Convolutional Sparse Coding with Low Rank Tensor

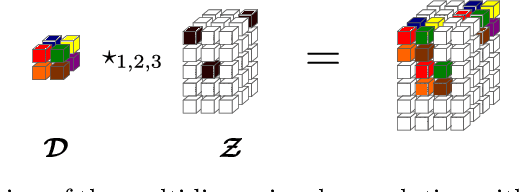
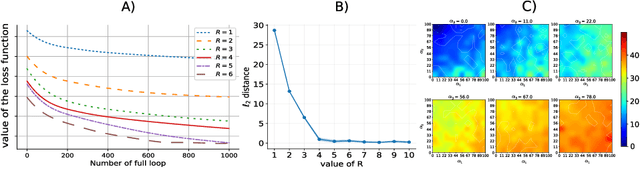
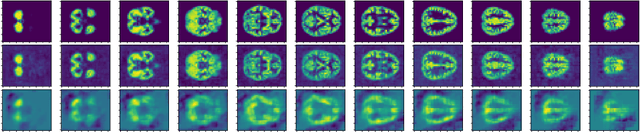
This paper introduces a new multivariate convolutional sparse coding based on tensor algebra with a general model enforcing both element-wise sparsity and low-rankness of the activations tensors. By using the CP decomposition, this model achieves a significantly more efficient encoding of the multivariate signal-particularly in the high order/ dimension setting-resulting in better performance. We prove that our model is closely related to the Kruskal tensor regression problem, offering interesting theoretical guarantees to our setting. Furthermore, we provide an efficient optimization algorithm based on alternating optimization to solve this model. Finally, we evaluate our algorithm with a large range of experiments, highlighting its advantages and limitations.

DICOD: Distributed Convolutional Sparse Coding

In this paper, we introduce DICOD, a convolutional sparse coding algorithm which builds shift invariant representations for long signals. This algorithm is designed to run in a distributed setting, with local message passing, making it communication efficient. It is based on coordinate descent and uses locally greedy updates which accelerate the resolution compared to greedy coordinate selection. We prove the convergence of this algorithm and highlight its computational speed-up which is super-linear in the number of cores used. We also provide empirical evidence for the acceleration properties of our algorithm compared to state-of-the-art methods.