Contrast-Free ICA and Causal Inference via Wasserstein Distances to the Gaussian

We study the squared $2$-Wasserstein distance to the standard Gaussian as a non-Gaussianity criterion and use it for linear Independent Component Analysis (ICA) and causal inference in Linear Non-Gaussian Acyclic Models (LiNGAM). The analysis relies on a strict inequality between the Wasserstein non-Gaussianity of independent standardized sources and that of their linear combinations. When at most one source is Gaussian, any unit-norm linear combination involving at least two sources has strictly smaller squared Wasserstein distance than the corresponding weighted sum of source distances. At the population level, this yields exact identification of the ICA unmixing matrix, up to signed permutation, and gives an analogous characterization of causal orders through least-squares residuals. We then define empirical plug-in estimators and prove distribution-free uniform convergence bounds under finite-moment assumptions, before detailing three practical solvers: a Picard-style orthogonal optimizer for ICA, an exhaustive dynamic program for causal-order search, and a greedy order-search variant. Empirically, we demonstrate competitive performance for both tasks and provide open-source implementations for source separation and causal inference.

Metric space valued Fréchet regression

We consider the problem of estimating the Fréchet and conditional Fréchet mean from data taking values in separable metric spaces. Unlike Euclidean spaces, where well-established methods are available, there is no practical estimator that works universally for all metric spaces. Therefore, we introduce a computable estimator for the Fréchet mean based on random quantization techniques and establish its universal consistency across any separable metric spaces. Additionally, we propose another estimator for the conditional Fréchet mean, leveraging data-driven partitioning and quantization, and demonstrate its universal consistency when the output space is any Banach space.

Online selective conformal inference: adaptive scores, convergence rate and optimality

In a supervised online setting, quantifying uncertainty has been proposed in the seminal work of \cite{gibbs2021adaptive}. For any given point-prediction algorithm, their method (ACI) produces a conformal prediction set with an average missed coverage getting close to a pre-specified level $\alpha$ for a long time horizon. We introduce an extended version of this algorithm, called OnlineSCI, allowing the user to additionally select times where such an inference should be made. OnlineSCI encompasses several prominent online selective tasks, such as building prediction intervals for extreme outcomes, classification with abstention, and online testing. While OnlineSCI controls the average missed coverage on the selected in an adversarial setting, our theoretical results also show that it controls the instantaneous error rate (IER) at the selected times, up to a non-asymptotical remainder term. Importantly, our theory covers the case where OnlineSCI updates the point-prediction algorithm at each time step, a property which we refer to as {\it adaptive} capability. We show that the adaptive versions of OnlineSCI can convergence to an optimal solution and provide an explicit convergence rate in each of the aforementioned application cases, under specific mild conditions. Finally, the favorable behavior of OnlineSCI in practice is illustrated by numerical experiments.

Transductive Conformal Inference for Ranking

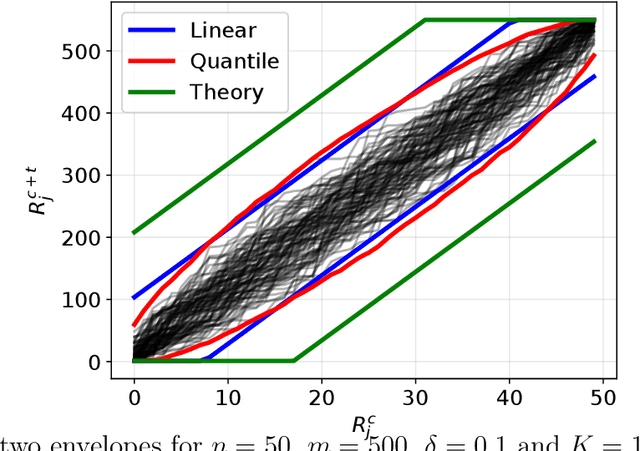
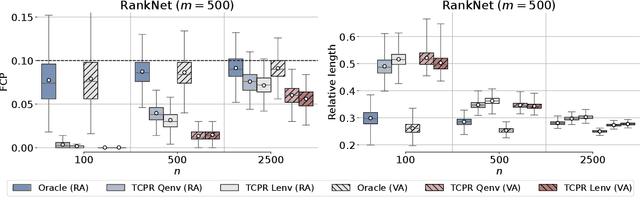
We introduce a method based on Conformal Prediction (CP) to quantify the uncertainty of full ranking algorithms. We focus on a specific scenario where $n + m$ items are to be ranked by some ''black box'' algorithm. It is assumed that the relative (ground truth) ranking of n of them is known. The objective is then to quantify the error made by the algorithm on the ranks of the m new items among the total $(n + m)$. In such a setting, the true ranks of the n original items in the total $(n + m)$ depend on the (unknown) true ranks of the m new ones. Consequently, we have no direct access to a calibration set to apply a classical CP method. To address this challenge, we propose to construct distribution-free bounds of the unknown conformity scores using recent results on the distribution of conformal p-values. Using these scores upper bounds, we provide valid prediction sets for the rank of any item. We also control the false coverage proportion, a crucial quantity when dealing with multiple prediction sets. Finally, we empirically show on both synthetic and real data the efficiency of our CP method.

Marginal and training-conditional guarantees in one-shot federated conformal prediction

We study conformal prediction in the one-shot federated learning setting. The main goal is to compute marginally and training-conditionally valid prediction sets, at the server-level, in only one round of communication between the agents and the server. Using the quantile-of-quantiles family of estimators and split conformal prediction, we introduce a collection of computationally-efficient and distribution-free algorithms that satisfy the aforementioned requirements. Our approaches come from theoretical results related to order statistics and the analysis of the Beta-Beta distribution. We also prove upper bounds on the coverage of all proposed algorithms when the nonconformity scores are almost surely distinct. For algorithms with training-conditional guarantees, these bounds are of the same order of magnitude as those of the centralized case. Remarkably, this implies that the one-shot federated learning setting entails no significant loss compared to the centralized case. Our experiments confirm that our algorithms return prediction sets with coverage and length similar to those obtained in a centralized setting.

One-Shot Federated Conformal Prediction

In this paper, we introduce a conformal prediction method to construct prediction sets in a oneshot federated learning setting. More specifically, we define a quantile-of-quantiles estimator and prove that for any distribution, it is possible to output prediction sets with desired coverage in only one round of communication. To mitigate privacy issues, we also describe a locally differentially private version of our estimator. Finally, over a wide range of experiments, we show that our method returns prediction sets with coverage and length very similar to those obtained in a centralized setting. Overall, these results demonstrate that our method is particularly well-suited to perform conformal predictions in a one-shot federated learning setting.

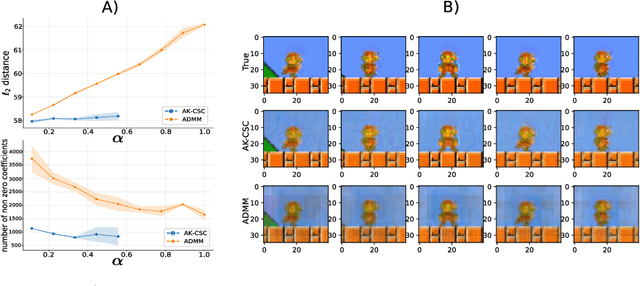
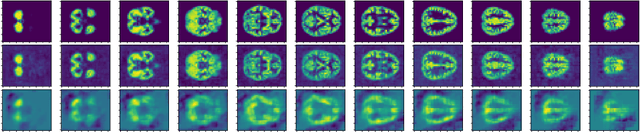
Tensor Convolutional Sparse Coding with Low-Rank activations, an application to EEG analysis

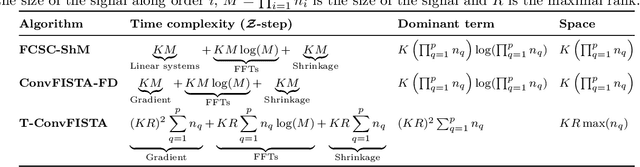
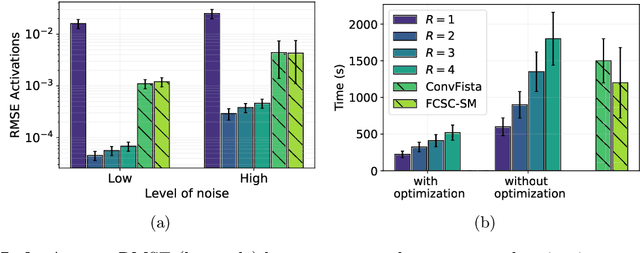
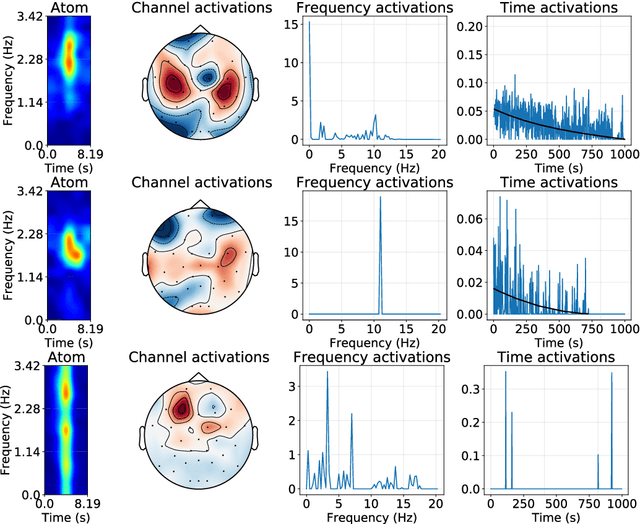
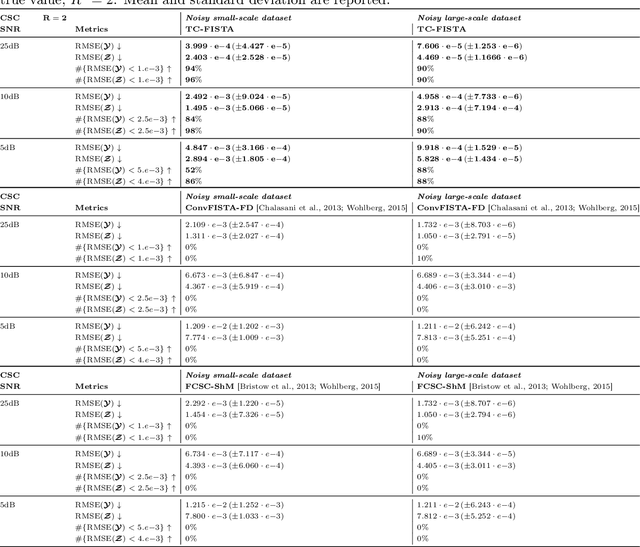
Recently, there has been growing interest in the analysis of spectrograms of ElectroEncephaloGram (EEG), particularly to study the neural correlates of (un)-consciousness during General Anesthesia (GA). Indeed, it has been shown that order three tensors (channels x frequencies x times) are a natural and useful representation of these signals. However this encoding entails significant difficulties, especially for convolutional sparse coding (CSC) as existing methods do not take advantage of the particularities of tensor representation, such as rank structures, and are vulnerable to the high level of noise and perturbations that are inherent to EEG during medical acts. To address this issue, in this paper we introduce a new CSC model, named Kruskal CSC (K-CSC), that uses the Kruskal decomposition of the activation tensors to leverage the intrinsic low rank nature of these representations in order to extract relevant and interpretable encodings. Our main contribution, TC-FISTA, uses multiple tools to efficiently solve the resulting optimization problem despite the increasing complexity induced by the tensor representation. We then evaluate TC-FISTA on both synthetic dataset and real EEG recorded during GA. The results show that TC-FISTA is robust to noise and perturbations, resulting in accurate, sparse and interpretable encoding of the signals.

Robust Kernel Density Estimation with Median-of-Means principle

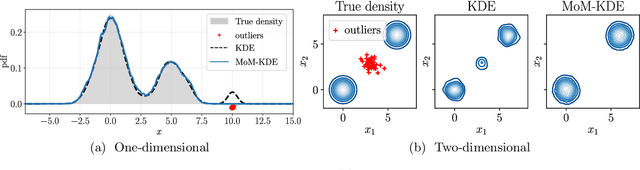
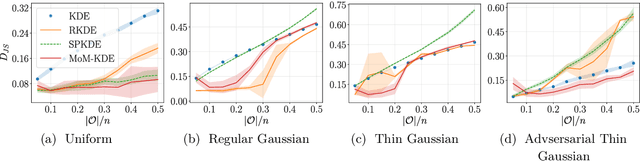
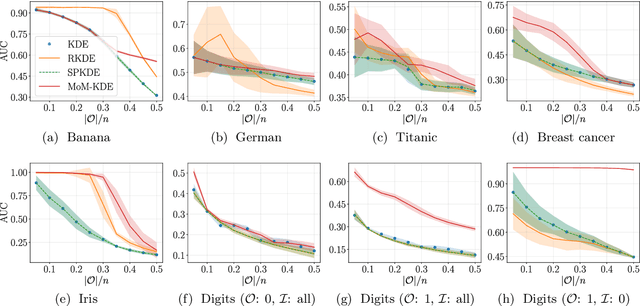
In this paper, we introduce a robust nonparametric density estimator combining the popular Kernel Density Estimation method and the Median-of-Means principle (MoM-KDE). This estimator is shown to achieve robustness to any kind of anomalous data, even in the case of adversarial contamination. In particular, while previous works only prove consistency results under known contamination model, this work provides finite-sample high-probability error-bounds without a priori knowledge on the outliers. Finally, when compared with other robust kernel estimators, we show that MoM-KDE achieves competitive results while having significant lower computational complexity.

Detecting multiple change-points in the time-varying Ising model

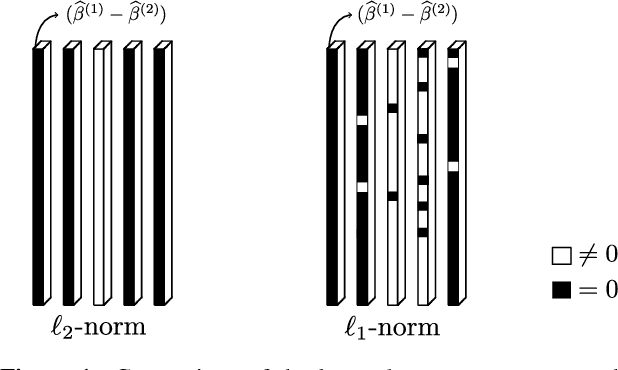
This work focuses on the estimation of change-points in a time-varying Ising graphical model (outputs $-1$ or $1$) evolving in a piecewise constant fashion. The occurring changes alter the graphical structure of the model, a structure which we also estimate in the present paper. For this purpose, we propose a new optimization program consisting in the minimization of a penalized negative conditional log-likelihood. The objective of the penalization is twofold: it imposes the learned graphs to be sparse and, thanks to a fused-type penalty, it enforces them to evolve piecewise constantly. Using few assumptions, we then give a change-point consistency theorem. Up to our knowledge, we are the first to present such theoretical result in the context of time-varying Ising model. Finally, experimental results on several synthetic examples and a real-world dataset demonstrate the empirical performance of our method.

Multivariate Convolutional Sparse Coding with Low Rank Tensor

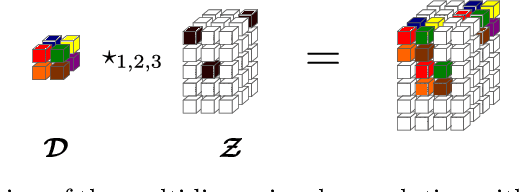
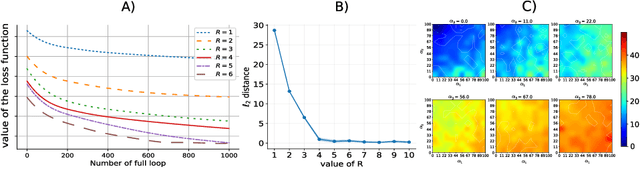
This paper introduces a new multivariate convolutional sparse coding based on tensor algebra with a general model enforcing both element-wise sparsity and low-rankness of the activations tensors. By using the CP decomposition, this model achieves a significantly more efficient encoding of the multivariate signal-particularly in the high order/ dimension setting-resulting in better performance. We prove that our model is closely related to the Kruskal tensor regression problem, offering interesting theoretical guarantees to our setting. Furthermore, we provide an efficient optimization algorithm based on alternating optimization to solve this model. Finally, we evaluate our algorithm with a large range of experiments, highlighting its advantages and limitations.