Julien Audiffren
CMLA
Extreme Multi-label Completion for Semantic Document Labelling with Taxonomy-Aware Parallel Learning
Dec 18, 2024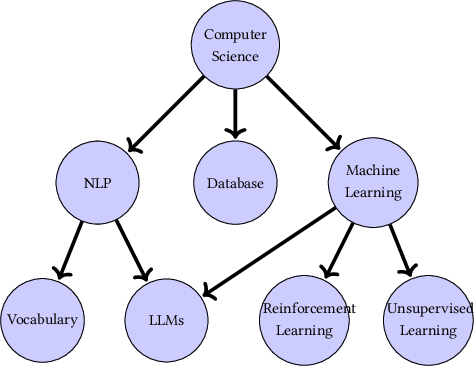
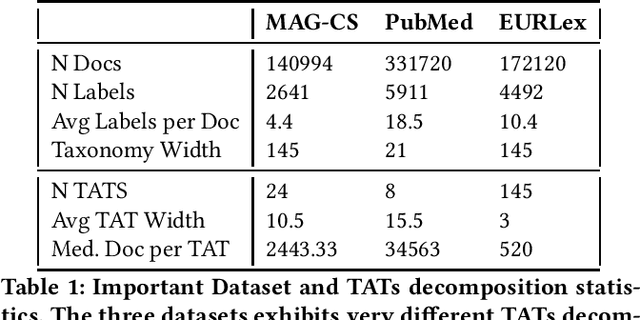
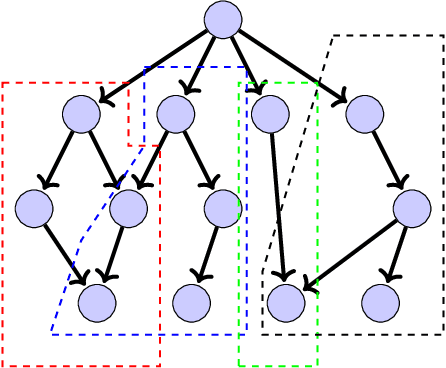
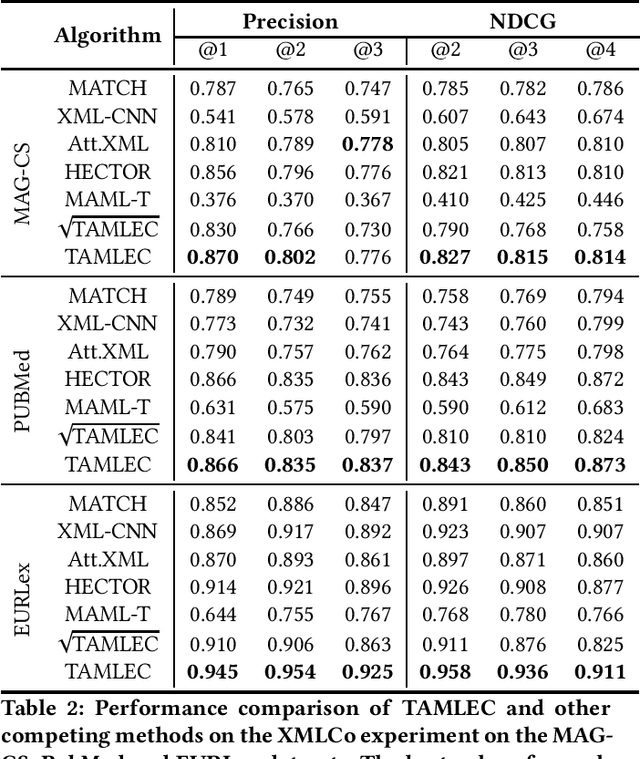
Abstract:In Extreme Multi Label Completion (XMLCo), the objective is to predict the missing labels of a collection of documents. Together with XML Classification, XMLCo is arguably one of the most challenging document classification tasks, as the very high number of labels (at least ten of thousands) is generally very large compared to the number of available labelled documents in the training dataset. Such a task is often accompanied by a taxonomy that encodes the labels organic relationships, and many methods have been proposed to leverage this hierarchy to improve the results of XMLCo algorithms. In this paper, we propose a new approach to this problem, TAMLEC (Taxonomy-Aware Multi-task Learning for Extreme multi-label Completion). TAMLEC divides the problem into several Taxonomy-Aware Tasks, i.e. subsets of labels adapted to the hierarchical paths of the taxonomy, and trains on these tasks using a dynamic Parallel Feature sharing approach, where some parts of the model are shared between tasks while others are task-specific. Then, at inference time, TAMLEC uses the labels available in a document to infer the appropriate tasks and to predict missing labels. To achieve this result, TAMLEC uses a modified transformer architecture that predicts ordered sequences of labels on a Weak-Semilattice structure that is naturally induced by the tasks. This approach yields multiple advantages. First, our experiments on real-world datasets show that TAMLEC outperforms state-of-the-art methods for various XMLCo problems. Second, TAMLEC is by construction particularly suited for few-shots XML tasks, where new tasks or labels are introduced with only few examples, and extensive evaluations highlight its strong performance compared to existing methods.
Tensor Convolutional Sparse Coding with Low-Rank activations, an application to EEG analysis
Jul 10, 2020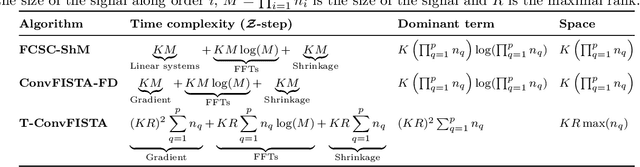
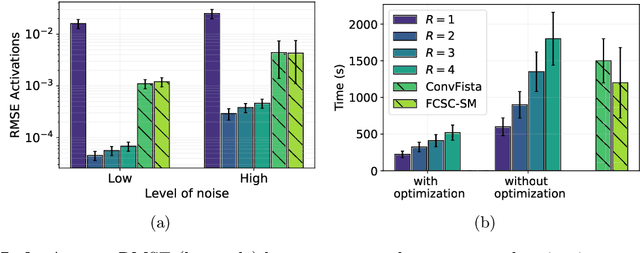
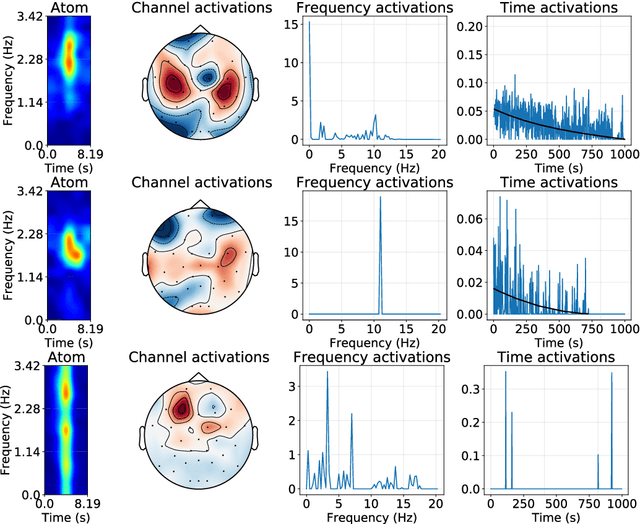
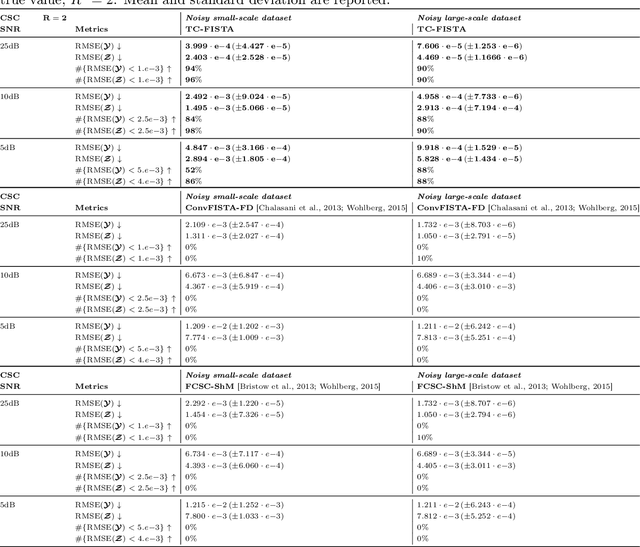
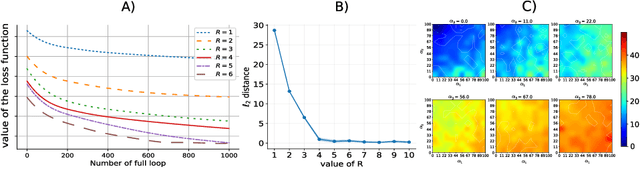
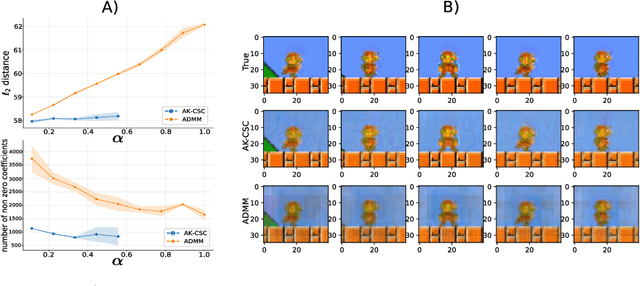
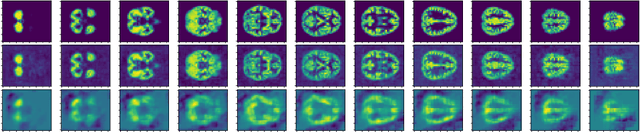
Abstract:Recently, there has been growing interest in the analysis of spectrograms of ElectroEncephaloGram (EEG), particularly to study the neural correlates of (un)-consciousness during General Anesthesia (GA). Indeed, it has been shown that order three tensors (channels x frequencies x times) are a natural and useful representation of these signals. However this encoding entails significant difficulties, especially for convolutional sparse coding (CSC) as existing methods do not take advantage of the particularities of tensor representation, such as rank structures, and are vulnerable to the high level of noise and perturbations that are inherent to EEG during medical acts. To address this issue, in this paper we introduce a new CSC model, named Kruskal CSC (K-CSC), that uses the Kruskal decomposition of the activation tensors to leverage the intrinsic low rank nature of these representations in order to extract relevant and interpretable encodings. Our main contribution, TC-FISTA, uses multiple tools to efficiently solve the resulting optimization problem despite the increasing complexity induced by the tensor representation. We then evaluate TC-FISTA on both synthetic dataset and real EEG recorded during GA. The results show that TC-FISTA is robust to noise and perturbations, resulting in accurate, sparse and interpretable encoding of the signals.
Fusing Vector Space Models for Domain-Specific Applications
Sep 05, 2019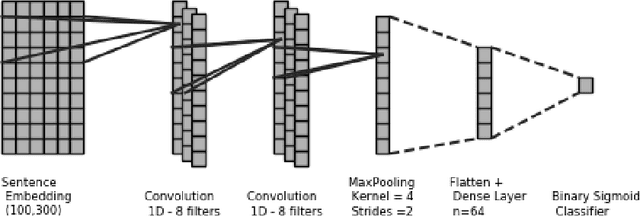
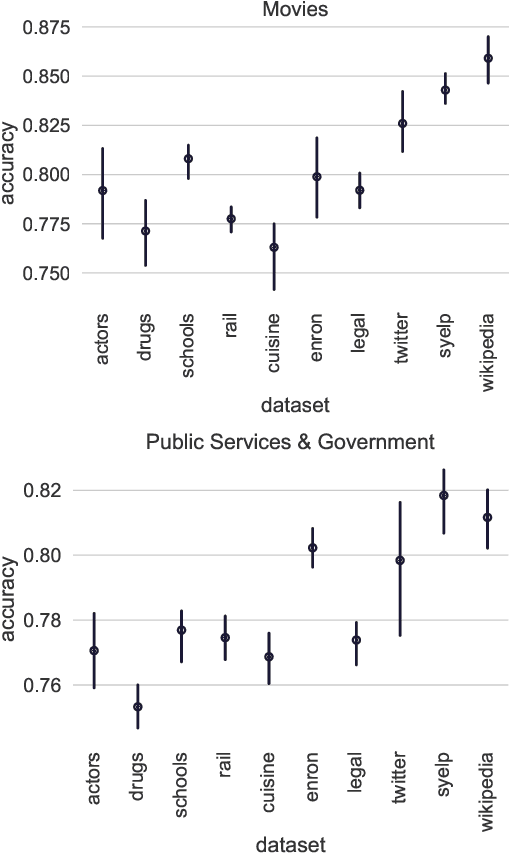
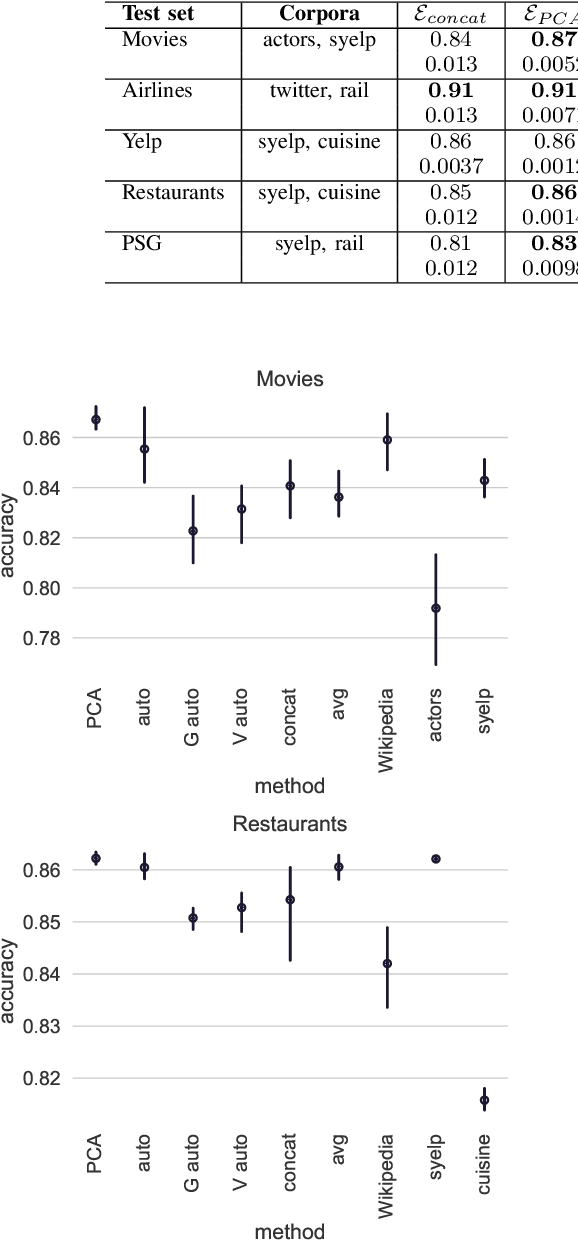
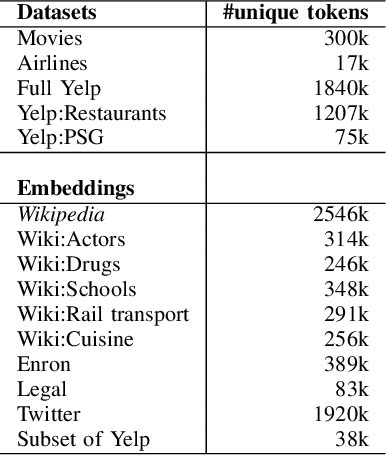
Abstract:We address the problem of tuning word embeddings for specific use cases and domains. We propose a new method that automatically combines multiple domain-specific embeddings, selected from a wide range of pre-trained domain-specific embeddings, to improve their combined expressive power. Our approach relies on two key components: 1) a ranking function, based on a new embedding similarity measure, that selects the most relevant embeddings to use given a domain and 2) a dimensionality reduction method that combines the selected embeddings to produce a more compact and efficient encoding that preserves the expressiveness. We empirically show that our method produces effective domain-specific embeddings that consistently improve the performance of state-of-the-art machine learning algorithms on multiple tasks, compared to generic embeddings trained on large text corpora.
Multivariate Convolutional Sparse Coding with Low Rank Tensor
Aug 09, 2019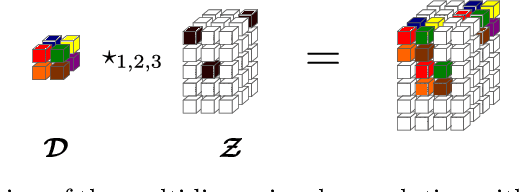
Abstract:This paper introduces a new multivariate convolutional sparse coding based on tensor algebra with a general model enforcing both element-wise sparsity and low-rankness of the activations tensors. By using the CP decomposition, this model achieves a significantly more efficient encoding of the multivariate signal-particularly in the high order/ dimension setting-resulting in better performance. We prove that our model is closely related to the Kruskal tensor regression problem, offering interesting theoretical guarantees to our setting. Furthermore, we provide an efficient optimization algorithm based on alternating optimization to solve this model. Finally, we evaluate our algorithm with a large range of experiments, highlighting its advantages and limitations.
Post Training in Deep Learning with Last Kernel
Oct 31, 2017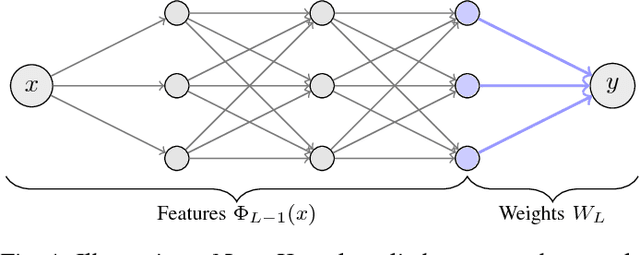
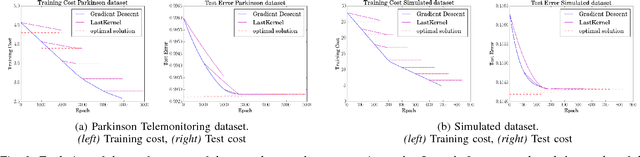
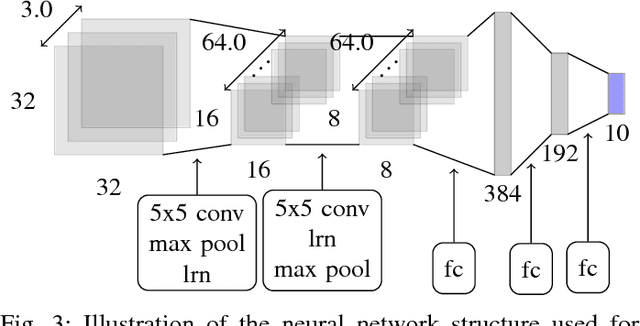
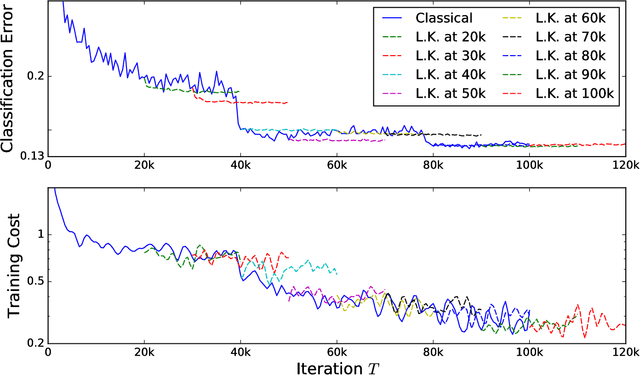
Abstract:One of the main challenges of deep learning methods is the choice of an appropriate training strategy. In particular, additional steps, such as unsupervised pre-training, have been shown to greatly improve the performances of deep structures. In this article, we propose an extra training step, called post-training, which only optimizes the last layer of the network. We show that this procedure can be analyzed in the context of kernel theory, with the first layers computing an embedding of the data and the last layer a statistical model to solve the task based on this embedding. This step makes sure that the embedding, or representation, of the data is used in the best possible way for the considered task. This idea is then tested on multiple architectures with various data sets, showing that it consistently provides a boost in performance.
M-Power Regularized Least Squares Regression
Dec 14, 2016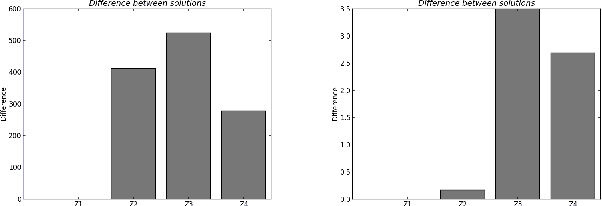
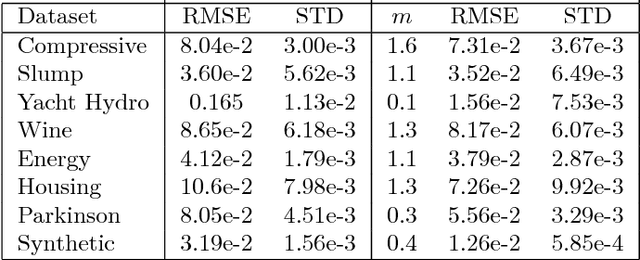

Abstract:Regularization is used to find a solution that both fits the data and is sufficiently smooth, and thereby is very effective for designing and refining learning algorithms. But the influence of its exponent remains poorly understood. In particular, it is unclear how the exponent of the reproducing kernel Hilbert space~(RKHS) regularization term affects the accuracy and the efficiency of kernel-based learning algorithms. Here we consider regularized least squares regression (RLSR) with an RKHS regularization raised to the power of m, where m is a variable real exponent. We design an efficient algorithm for solving the associated minimization problem, we provide a theoretical analysis of its stability, and we compare its advantage with respect to computational complexity, speed of convergence and prediction accuracy to the classical kernel ridge regression algorithm where the regularization exponent m is fixed at 2. Our results show that the m-power RLSR problem can be solved efficiently, and support the suggestion that one can use a regularization term that grows significantly slower than the standard quadratic growth in the RKHS norm.
Operator-valued Kernels for Learning from Functional Response Data
Nov 02, 2016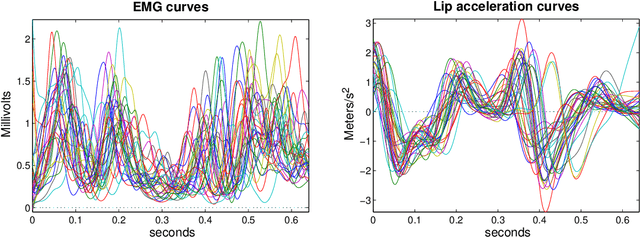
Abstract:In this paper we consider the problems of supervised classification and regression in the case where attributes and labels are functions: a data is represented by a set of functions, and the label is also a function. We focus on the use of reproducing kernel Hilbert space theory to learn from such functional data. Basic concepts and properties of kernel-based learning are extended to include the estimation of function-valued functions. In this setting, the representer theorem is restated, a set of rigorously defined infinite-dimensional operator-valued kernels that can be valuably applied when the data are functions is described, and a learning algorithm for nonlinear functional data analysis is introduced. The methodology is illustrated through speech and audio signal processing experiments.
* in Journal of Machine Learning Research (JMLR), 2016
Decoy Bandits Dueling on a Poset
Jun 09, 2016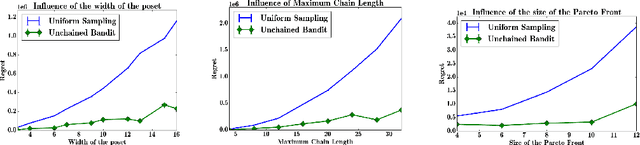

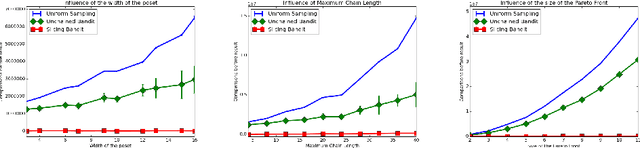
Abstract:We adress the problem of dueling bandits defined on partially ordered sets, or posets. In this setting, arms may not be comparable, and there may be several (incomparable) optimal arms. We propose an algorithm, UnchainedBandits, that efficiently finds the set of optimal arms of any poset even when pairs of comparable arms cannot be distinguished from pairs of incomparable arms, with a set of minimal assumptions. This algorithm relies on the concept of decoys, which stems from social psychology. For the easier case where the incomparability information may be accessible, we propose a second algorithm, SlicingBandits, which takes advantage of this information and achieves a very significant gain of performance compared to UnchainedBandits. We provide theoretical guarantees and experimental evaluation for both algorithms.
Stationary Mixing Bandits
Jun 23, 2014Abstract:We study the bandit problem where arms are associated with stationary phi-mixing processes and where rewards are therefore dependent: the question that arises from this setting is that of recovering some independence by ignoring the value of some rewards. As we shall see, the bandit problem we tackle requires us to address the exploration/exploitation/independence trade-off. To do so, we provide a UCB strategy together with a general regret analysis for the case where the size of the independence blocks (the ignored rewards) is fixed and we go a step beyond by providing an algorithm that is able to compute the size of the independence blocks from the data. Finally, we give an analysis of our bandit problem in the restless case, i.e., in the situation where the time counters for all mixing processes simultaneously evolve.
Equivalence of Learning Algorithms
Jun 10, 2014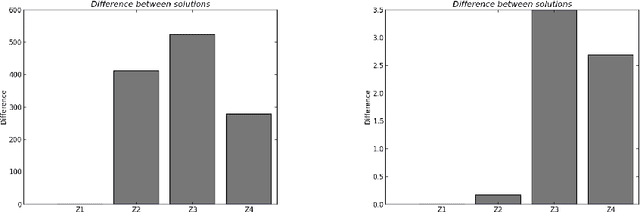
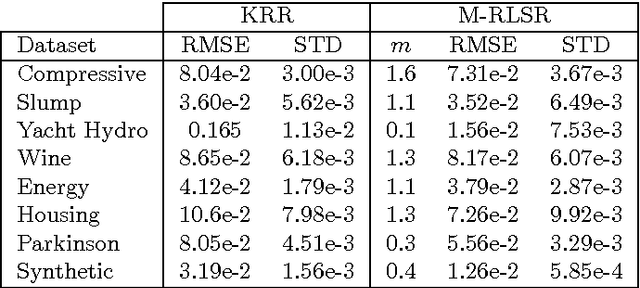
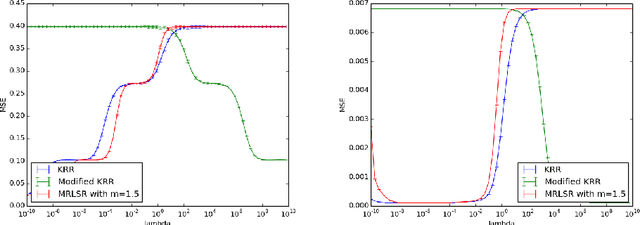
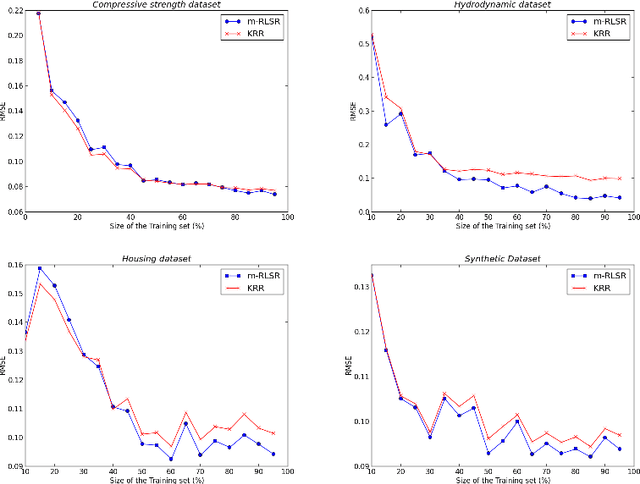
Abstract:The purpose of this paper is to introduce a concept of equivalence between machine learning algorithms. We define two notions of algorithmic equivalence, namely, weak and strong equivalence. These notions are of paramount importance for identifying when learning prop erties from one learning algorithm can be transferred to another. Using regularized kernel machines as a case study, we illustrate the importance of the introduced equivalence concept by analyzing the relation between kernel ridge regression (KRR) and m-power regularized least squares regression (M-RLSR) algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge