Decoy Bandits Dueling on a Poset

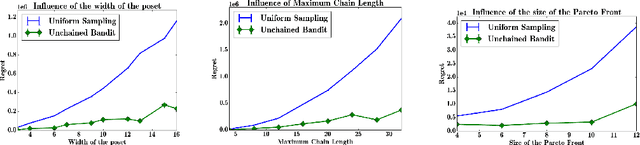
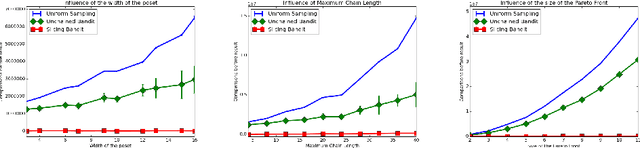
We adress the problem of dueling bandits defined on partially ordered sets, or posets. In this setting, arms may not be comparable, and there may be several (incomparable) optimal arms. We propose an algorithm, UnchainedBandits, that efficiently finds the set of optimal arms of any poset even when pairs of comparable arms cannot be distinguished from pairs of incomparable arms, with a set of minimal assumptions. This algorithm relies on the concept of decoys, which stems from social psychology. For the easier case where the incomparability information may be accessible, we propose a second algorithm, SlicingBandits, which takes advantage of this information and achieves a very significant gain of performance compared to UnchainedBandits. We provide theoretical guarantees and experimental evaluation for both algorithms.