Spectral Truncation Kernels: Noncommutativity in $C^*$-algebraic Kernel Machines

In this paper, we propose a new class of positive definite kernels based on the spectral truncation, which has been discussed in the fields of noncommutative geometry and $C^*$-algebra. We focus on kernels whose inputs and outputs are functions and generalize existing kernels, such as polynomial, product, and separable kernels, by introducing a truncation parameter $n$ that describes the noncommutativity of the products appearing in the kernels. When $n$ goes to infinity, the proposed kernels tend to the existing commutative kernels. If $n$ is finite, they exhibit different behavior, and the noncommutativity induces interactions along the data function domain. We show that the truncation parameter $n$ is a governing factor leading to performance enhancement: by setting an appropriate $n$, we can balance the representation power and the complexity of the representation space. The flexibility of the proposed class of kernels allows us to go beyond previous commutative kernels.

$C^*$-Algebraic Machine Learning: Moving in a New Direction

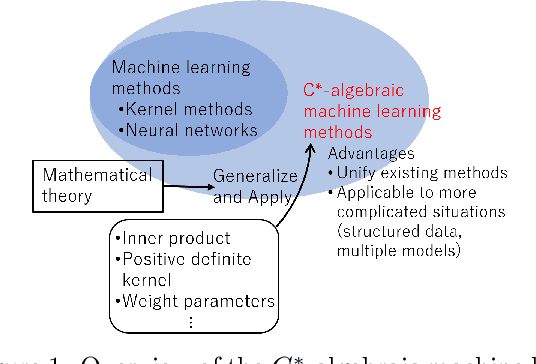
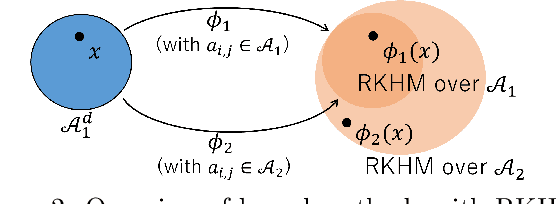
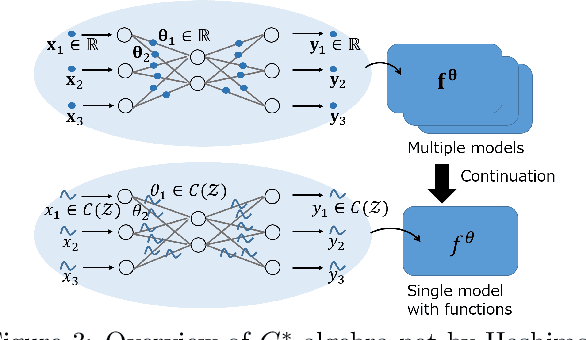
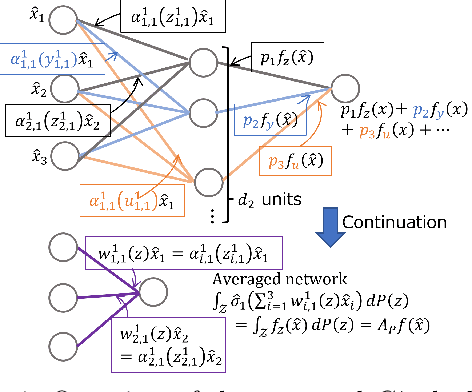
Machine learning has a long collaborative tradition with several fields of mathematics, such as statistics, probability and linear algebra. We propose a new direction for machine learning research: $C^*$-algebraic ML $-$ a cross-fertilization between $C^*$-algebra and machine learning. The mathematical concept of $C^*$-algebra is a natural generalization of the space of complex numbers. It enables us to unify existing learning strategies, and construct a new framework for more diverse and information-rich data models. We explain why and how to use $C^*$-algebras in machine learning, and provide technical considerations that go into the design of $C^*$-algebraic learning models in the contexts of kernel methods and neural networks. Furthermore, we discuss open questions and challenges in $C^*$-algebraic ML and give our thoughts for future development and applications.

Orthogonal Random Features: Explicit Forms and Sharp Inequalities

Random features have been introduced to scale up kernel methods via randomization techniques. In particular, random Fourier features and orthogonal random features were used to approximate the popular Gaussian kernel. The former is performed by a random Gaussian matrix and leads exactly to the Gaussian kernel after averaging. In this work, we analyze the bias and the variance of the kernel approximation based on orthogonal random features which makes use of Haar orthogonal matrices. We provide explicit expressions for these quantities using normalized Bessel functions and derive sharp exponential bounds supporting the view that orthogonal random features are more informative than random Fourier features.

Large-Scale Quantum Separability Through a Reproducible Machine Learning Lens

The quantum separability problem consists in deciding whether a bipartite density matrix is entangled or separable. In this work, we propose a machine learning pipeline for finding approximate solutions for this NP-hard problem in large-scale scenarios. We provide an efficient Frank-Wolfe-based algorithm to approximately seek the nearest separable density matrix and derive a systematic way for labeling density matrices as separable or entangled, allowing us to treat quantum separability as a classification problem. Our method is applicable to any two-qudit mixed states. Numerical experiments with quantum states of 3- and 7-dimensional qudits validate the efficiency of the proposed procedure, and demonstrate that it scales up to thousands of density matrices with a high quantum entanglement detection accuracy. This takes a step towards benchmarking quantum separability to support the development of more powerful entanglement detection techniques.

Deep Learning with Kernels through RKHM and the Perron-Frobenius Operator

Reproducing kernel Hilbert $C^*$-module (RKHM) is a generalization of reproducing kernel Hilbert space (RKHS) by means of $C^*$-algebra, and the Perron-Frobenius operator is a linear operator related to the composition of functions. Combining these two concepts, we present deep RKHM, a deep learning framework for kernel methods. We derive a new Rademacher generalization bound in this setting and provide a theoretical interpretation of benign overfitting by means of Perron-Frobenius operators. By virtue of $C^*$-algebra, the dependency of the bound on output dimension is milder than existing bounds. We show that $C^*$-algebra is a suitable tool for deep learning with kernels, enabling us to take advantage of the product structure of operators and to provide a clear connection with convolutional neural networks. Our theoretical analysis provides a new lens through which one can design and analyze deep kernel methods.

Implicit Regularization with Polynomial Growth in Deep Tensor Factorization

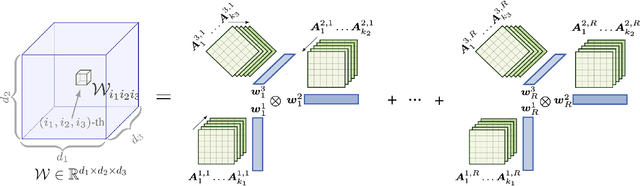
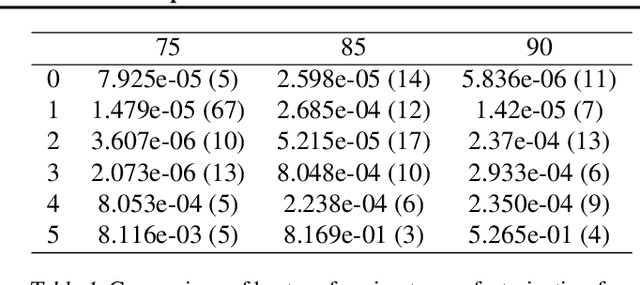
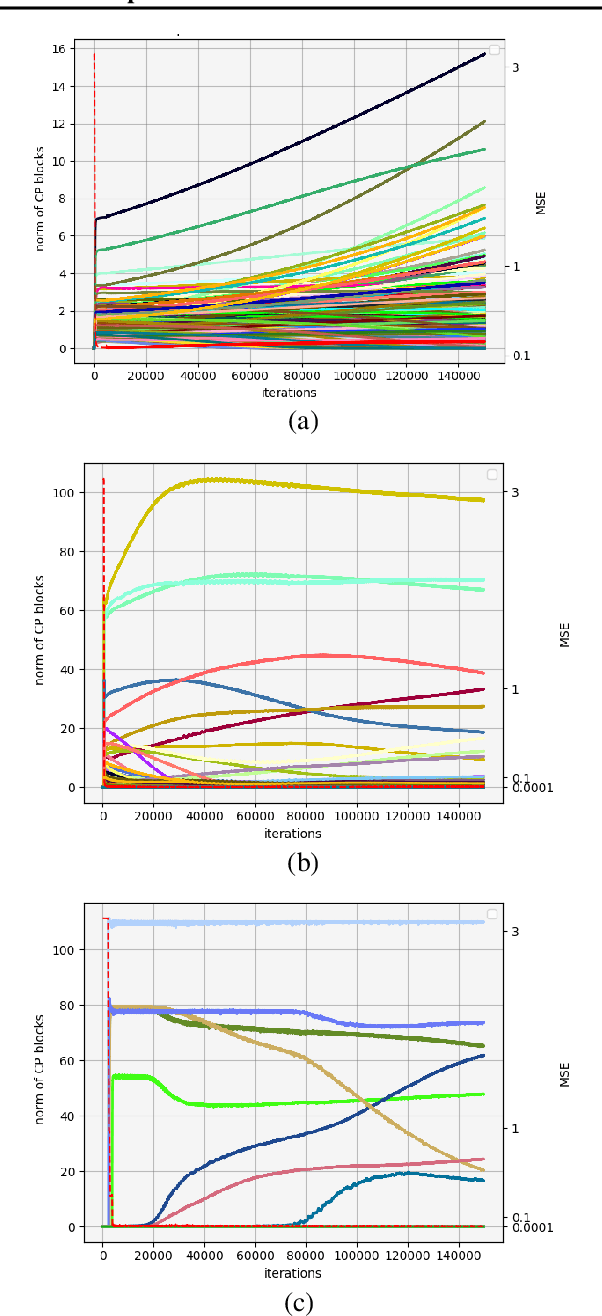
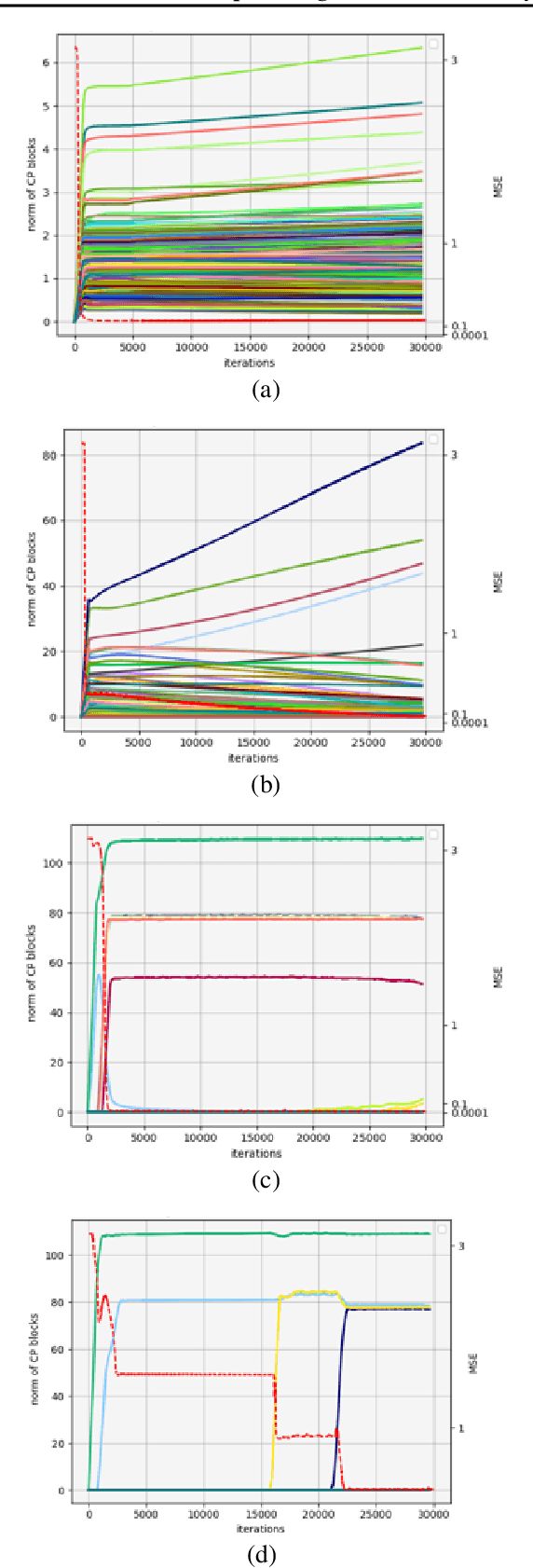
We study the implicit regularization effects of deep learning in tensor factorization. While implicit regularization in deep matrix and 'shallow' tensor factorization via linear and certain type of non-linear neural networks promotes low-rank solutions with at most quadratic growth, we show that its effect in deep tensor factorization grows polynomially with the depth of the network. This provides a remarkably faithful description of the observed experimental behaviour. Using numerical experiments, we demonstrate the benefits of this implicit regularization in yielding a more accurate estimation and better convergence properties.

Learning primal-dual sparse kernel machines

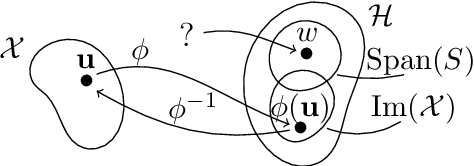
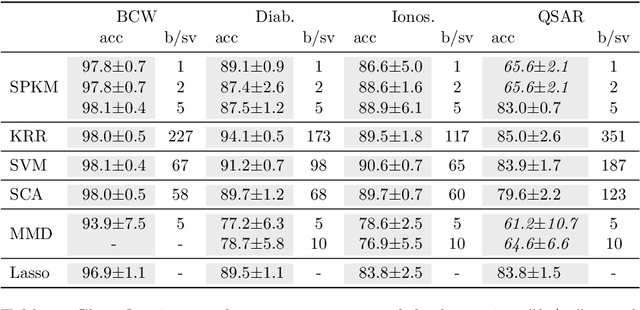
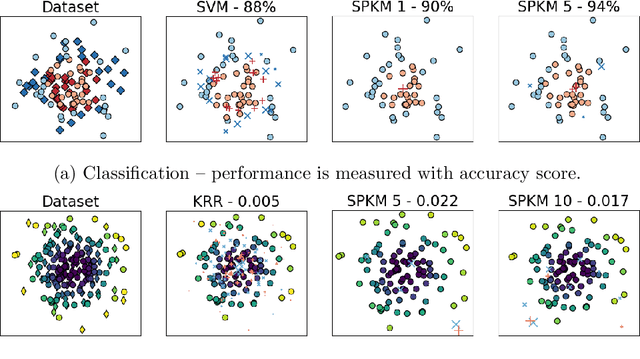
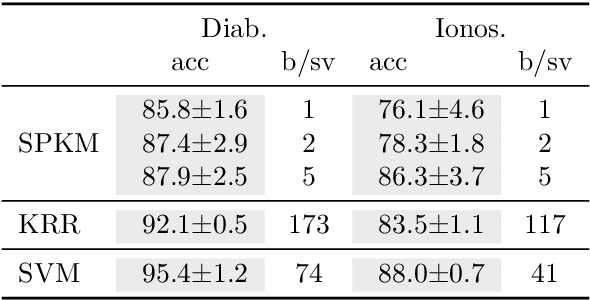
Traditionally, kernel methods rely on the representer theorem which states that the solution to a learning problem is obtained as a linear combination of the data mapped into the reproducing kernel Hilbert space (RKHS). While elegant from theoretical point of view, the theorem is prohibitive for algorithms' scalability to large datasets, and the interpretability of the learned function. In this paper, instead of using the traditional representer theorem, we propose to search for a solution in RKHS that has a pre-image decomposition in the original data space, where the elements don't necessarily correspond to the elements in the training set. Our gradient-based optimisation method then hinges on optimising over possibly sparse elements in the input space, and enables us to obtain a kernel-based model with both primal and dual sparsity. We give theoretical justification on the proposed method's generalization ability via a Rademacher bound. Our experiments demonstrate a better scalability and interpretability with accuracy on par with the traditional kernel-based models.

Quantum Perceptron Revisited: Computational-Statistical Tradeoffs

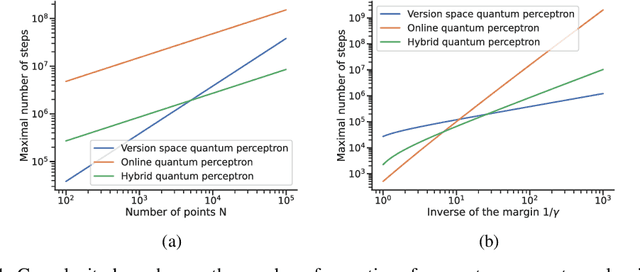
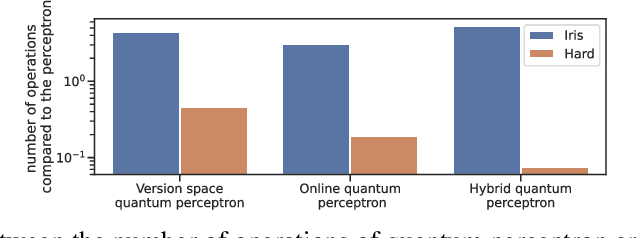
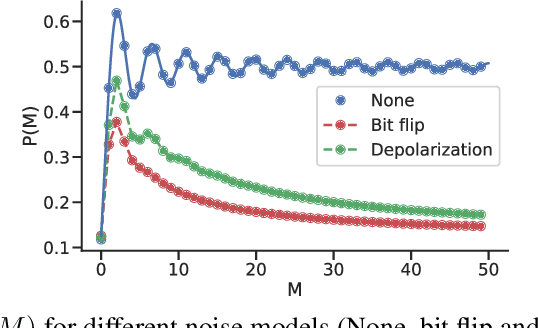
Quantum machine learning algorithms could provide significant speed-ups over their classical counterparts; however, whether they could also achieve good generalization remains unclear. Recently, two quantum perceptron models which give a quadratic improvement over the classical perceptron algorithm using Grover's search have been proposed by Wiebe et al. arXiv:1602.04799 . While the first model reduces the complexity with respect to the size of the training set, the second one improves the bound on the number of mistakes made by the perceptron. In this paper, we introduce a hybrid quantum-classical perceptron algorithm with lower complexity and better generalization ability than the classical perceptron. We show a quadratic improvement over the classical perceptron in both the number of samples and the margin of the data. We derive a bound on the expected error of the hypothesis returned by our algorithm, which compares favorably to the one obtained with the classical online perceptron. We use numerical experiments to illustrate the trade-off between computational complexity and statistical accuracy in quantum perceptron learning and discuss some of the key practical issues surrounding the implementation of quantum perceptron models into near-term quantum devices, whose practical implementation represents a serious challenge due to inherent noise. However, the potential benefits make correcting this worthwhile.

Implicit Regularization in Deep Tensor Factorization

Attempts of studying implicit regularization associated to gradient descent (GD) have identified matrix completion as a suitable test-bed. Late findings suggest that this phenomenon cannot be phrased as a minimization-norm problem, implying that a paradigm shift is required and that dynamics has to be taken into account. In the present work we address the more general setup of tensor completion by leveraging two popularized tensor factorization, namely Tucker and TensorTrain (TT). We track relevant quantities such as tensor nuclear norm, effective rank, generalized singular values and we introduce deep Tucker and TT unconstrained factorization to deal with the completion task. Experiments on both synthetic and real data show that gradient descent promotes solution with low-rank, and validate the conjecture saying that the phenomenon has to be addressed from a dynamical perspective.

Entangled Kernels -- Beyond Separability

We consider the problem of operator-valued kernel learning and investigate the possibility of going beyond the well-known separable kernels. Borrowing tools and concepts from the field of quantum computing, such as partial trace and entanglement, we propose a new view on operator-valued kernels and define a general family of kernels that encompasses previously known operator-valued kernels, including separable and transformable kernels. Within this framework, we introduce another novel class of operator-valued kernels called entangled kernels that are not separable. We propose an efficient two-step algorithm for this framework, where the entangled kernel is learned based on a novel extension of kernel alignment to operator-valued kernels. We illustrate our algorithm with an application to supervised dimensionality reduction, and demonstrate its effectiveness with both artificial and real data for multi-output regression.