Yuka Hashimoto
Why High-rank Neural Networks Generalize?: An Algebraic Framework with RKHSs
Sep 26, 2025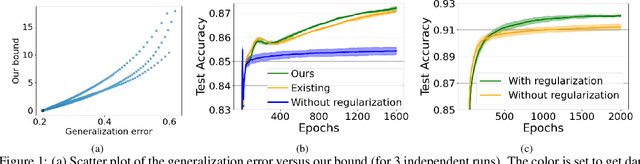
Abstract:We derive a new Rademacher complexity bound for deep neural networks using Koopman operators, group representations, and reproducing kernel Hilbert spaces (RKHSs). The proposed bound describes why the models with high-rank weight matrices generalize well. Although there are existing bounds that attempt to describe this phenomenon, these existing bounds can be applied to limited types of models. We introduce an algebraic representation of neural networks and a kernel function to construct an RKHS to derive a bound for a wider range of realistic models. This work paves the way for the Koopman-based theory for Rademacher complexity bounds to be valid for more practical situations.
Towards Quantum Operator-Valued Kernels
Jun 04, 2025Abstract:Quantum kernels are reproducing kernel functions built using quantum-mechanical principles and are studied with the aim of outperforming their classical counterparts. The enthusiasm for quantum kernel machines has been tempered by recent studies that have suggested that quantum kernels could not offer speed-ups when learning on classical data. However, most of the research in this area has been devoted to scalar-valued kernels in standard classification or regression settings for which classical kernel methods are efficient and effective, leaving very little room for improvement with quantum kernels. This position paper argues that quantum kernel research should focus on more expressive kernel classes. We build upon recent advances in operator-valued kernels, and propose guidelines for investigating quantum kernels. This should help to design a new generation of quantum kernel machines and fully explore their potentials.
Generalization Through Growth: Hidden Dynamics Controls Depth Dependence
May 21, 2025Abstract:Recent theory has reduced the depth dependence of generalization bounds from exponential to polynomial and even depth-independent rates, yet these results remain tied to specific architectures and Euclidean inputs. We present a unified framework for arbitrary \blue{pseudo-metric} spaces in which a depth-\(k\) network is the composition of continuous hidden maps \(f:\mathcal{X}\to \mathcal{X}\) and an output map \(h:\mathcal{X}\to \mathbb{R}\). The resulting bound $O(\sqrt{(\alpha + \log \beta(k))/n})$ isolates the sole depth contribution in \(\beta(k)\), the word-ball growth of the semigroup generated by the hidden layers. By Gromov's theorem polynomial (resp. exponential) growth corresponds to virtually nilpotent (resp. expanding) dynamics, revealing a geometric dichotomy behind existing $O(\sqrt{k})$ (sublinear depth) and $\tilde{O}(1)$ (depth-independent) rates. We further provide covering-number estimates showing that expanding dynamics yield an exponential parameter saving via compositional expressivity. Our results decouple specification from implementation, offering architecture-agnostic and dynamical-systems-aware guarantees applicable to modern deep-learning paradigms such as test-time inference and diffusion models.
Deep Koopman-layered Model with Universal Property Based on Toeplitz Matrices
Oct 03, 2024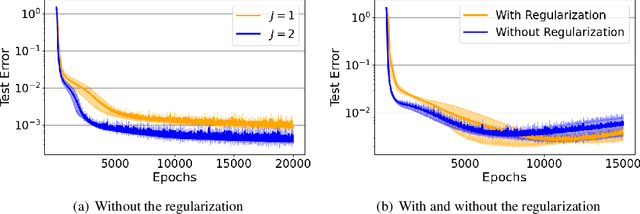
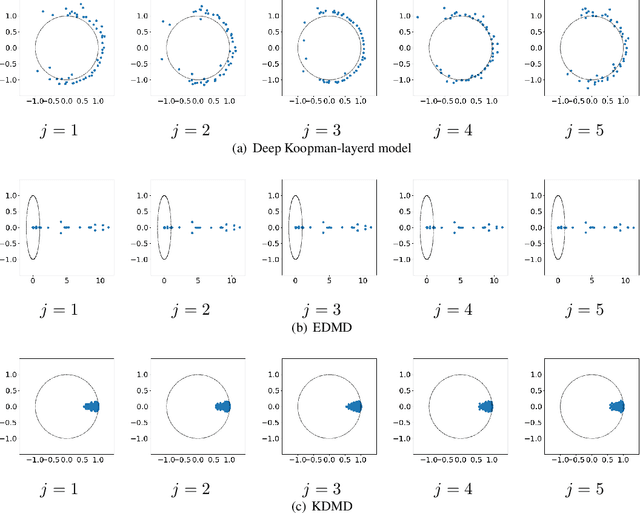
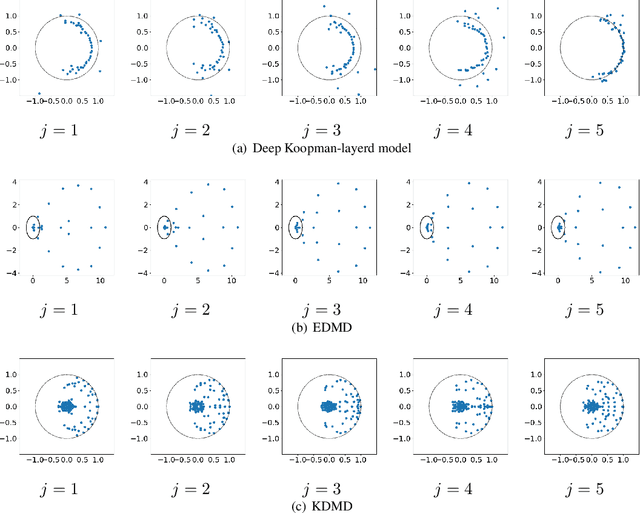
Abstract:We propose deep Koopman-layered models with learnable parameters in the form of Toeplitz matrices for analyzing the dynamics of time-series data. The proposed model has both theoretical solidness and flexibility. By virtue of the universal property of Toeplitz matrices and the reproducing property underlined in the model, we can show its universality and the generalization property. In addition, the flexibility of the proposed model enables the model to fit time-series data coming from nonautonomous dynamical systems. When training the model, we apply Krylov subspace methods for efficient computations. In addition, the proposed model can be regarded as a neural ODE-based model. In this sense, the proposed model establishes a new connection among Koopman operators, neural ODEs, and numerical linear algebraic methods.
Spectral Truncation Kernels: Noncommutativity in $C^*$-algebraic Kernel Machines
May 28, 2024


Abstract:In this paper, we propose a new class of positive definite kernels based on the spectral truncation, which has been discussed in the fields of noncommutative geometry and $C^*$-algebra. We focus on kernels whose inputs and outputs are functions and generalize existing kernels, such as polynomial, product, and separable kernels, by introducing a truncation parameter $n$ that describes the noncommutativity of the products appearing in the kernels. When $n$ goes to infinity, the proposed kernels tend to the existing commutative kernels. If $n$ is finite, they exhibit different behavior, and the noncommutativity induces interactions along the data function domain. We show that the truncation parameter $n$ is a governing factor leading to performance enhancement: by setting an appropriate $n$, we can balance the representation power and the complexity of the representation space. The flexibility of the proposed class of kernels allows us to go beyond previous commutative kernels.
Constructive Universal Approximation Theorems for Deep Joint-Equivariant Networks by Schur's Lemma
May 22, 2024

Abstract:We present a unified constructive universal approximation theorem covering a wide range of learning machines including both shallow and deep neural networks based on the group representation theory. Constructive here means that the distribution of parameters is given in a closed-form expression (called the ridgelet transform). Contrary to the case of shallow models, expressive power analysis of deep models has been conducted in a case-by-case manner. Recently, Sonoda et al. (2023a,b) developed a systematic method to show a constructive approximation theorem from scalar-valued joint-group-invariant feature maps, covering a formal deep network. However, each hidden layer was formalized as an abstract group action, so it was not possible to cover real deep networks defined by composites of nonlinear activation function. In this study, we extend the method for vector-valued joint-group-equivariant feature maps, so to cover such real networks.
Quantum Circuit $C^*$-algebra Net
Apr 09, 2024



Abstract:This paper introduces quantum circuit $C^*$-algebra net, which provides a connection between $C^*$-algebra nets proposed in classical machine learning and quantum circuits. Using $C^*$-algebra, a generalization of the space of complex numbers, we can represent quantum gates as weight parameters of a neural network. By introducing additional parameters, we can induce interaction among multiple circuits constructed by quantum gates. This interaction enables the circuits to share information among them, which contributes to improved generalization performance in machine learning tasks. As an application, we propose to use the quantum circuit $C^*$-algebra net to encode classical data into quantum states, which enables us to integrate classical data into quantum algorithms. Numerical results demonstrate that the interaction among circuits improves performance significantly in image classification, and encoded data by the quantum circuit $C^*$-algebra net are useful for downstream quantum machine learning tasks.
Koopman operators with intrinsic observables in rigged reproducing kernel Hilbert spaces
Mar 14, 2024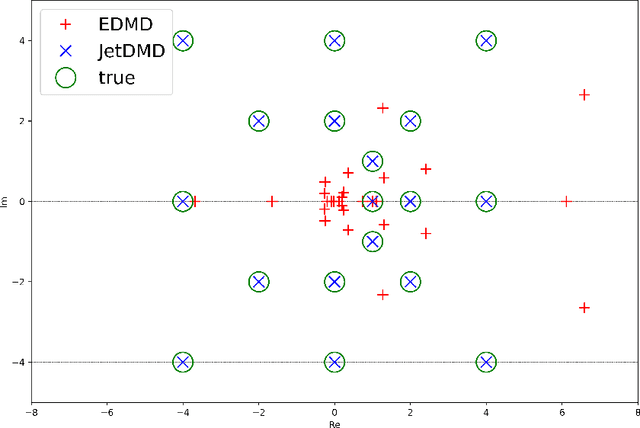
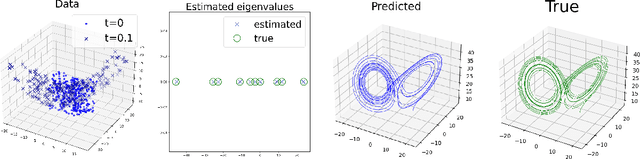
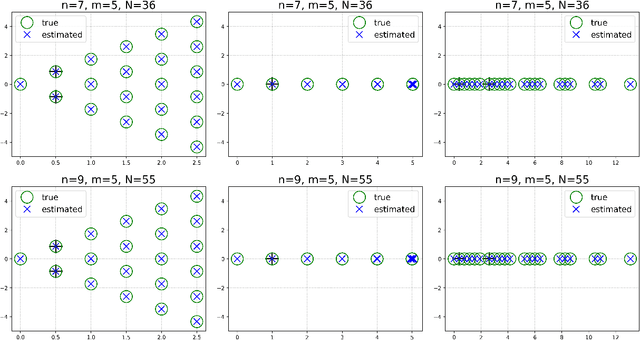
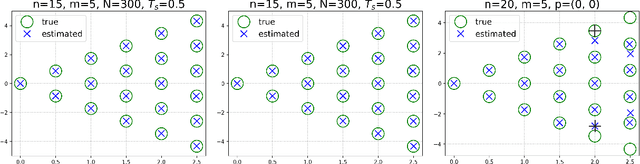
Abstract:This paper presents a novel approach for estimating the Koopman operator defined on a reproducing kernel Hilbert space (RKHS) and its spectra. We propose an estimation method, what we call Jet Dynamic Mode Decomposition (JetDMD), leveraging the intrinsic structure of RKHS and the geometric notion known as jets to enhance the estimation of the Koopman operator. This method refines the traditional Extended Dynamic Mode Decomposition (EDMD) in accuracy, especially in the numerical estimation of eigenvalues. This paper proves JetDMD's superiority through explicit error bounds and convergence rate for special positive definite kernels, offering a solid theoretical foundation for its performance. We also delve into the spectral analysis of the Koopman operator, proposing the notion of extended Koopman operator within a framework of rigged Hilbert space. This notion leads to a deeper understanding of estimated Koopman eigenfunctions and capturing them outside the original function space. Through the theory of rigged Hilbert space, our study provides a principled methodology to analyze the estimated spectrum and eigenfunctions of Koopman operators, and enables eigendecomposition within a rigged RKHS. We also propose a new effective method for reconstructing the dynamical system from temporally-sampled trajectory data of the dynamical system with solid theoretical guarantee. We conduct several numerical simulations using the van der Pol oscillator, the Duffing oscillator, the H\'enon map, and the Lorenz attractor, and illustrate the performance of JetDMD with clear numerical computations of eigenvalues and accurate predictions of the dynamical systems.
$C^*$-Algebraic Machine Learning: Moving in a New Direction
Feb 04, 2024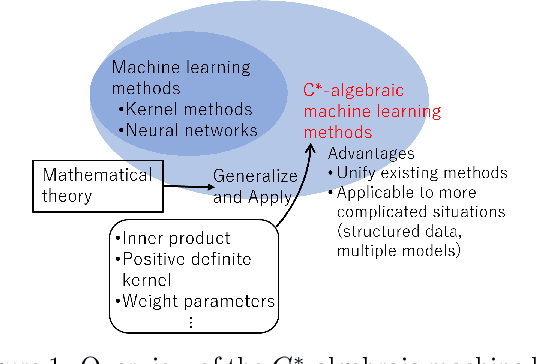
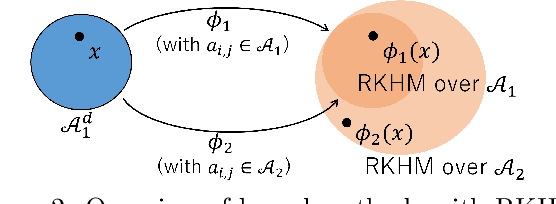
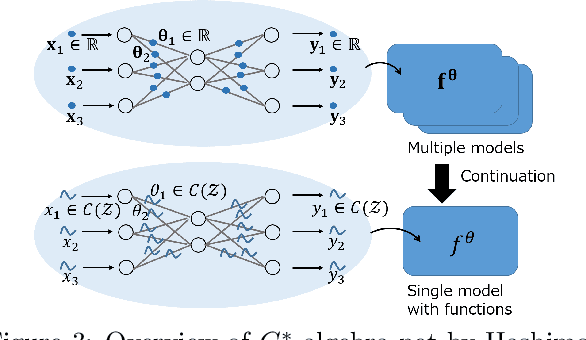
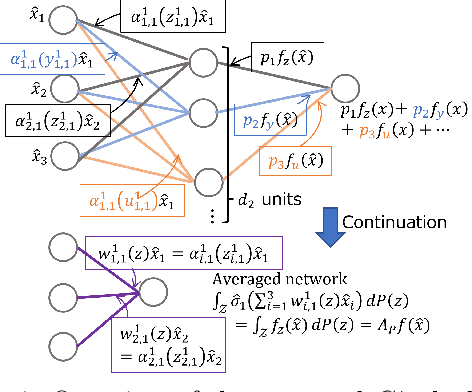
Abstract:Machine learning has a long collaborative tradition with several fields of mathematics, such as statistics, probability and linear algebra. We propose a new direction for machine learning research: $C^*$-algebraic ML $-$ a cross-fertilization between $C^*$-algebra and machine learning. The mathematical concept of $C^*$-algebra is a natural generalization of the space of complex numbers. It enables us to unify existing learning strategies, and construct a new framework for more diverse and information-rich data models. We explain why and how to use $C^*$-algebras in machine learning, and provide technical considerations that go into the design of $C^*$-algebraic learning models in the contexts of kernel methods and neural networks. Furthermore, we discuss open questions and challenges in $C^*$-algebraic ML and give our thoughts for future development and applications.
Deep Ridgelet Transform: Voice with Koopman Operator Proves Universality of Formal Deep Networks
Oct 05, 2023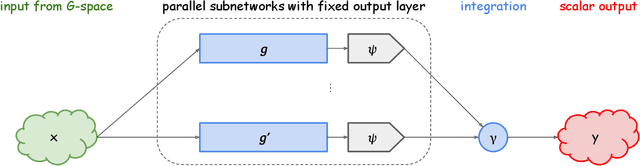
Abstract:We identify hidden layers inside a DNN with group actions on the data space, and formulate the DNN as a dual voice transform with respect to Koopman operator, a linear representation of the group action. Based on the group theoretic arguments, particularly by using Schur's lemma, we show a simple proof of the universality of those DNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge