Deep Ridgelet Transform: Voice with Koopman Operator Proves Universality of Formal Deep Networks
Paper and Code
Oct 05, 2023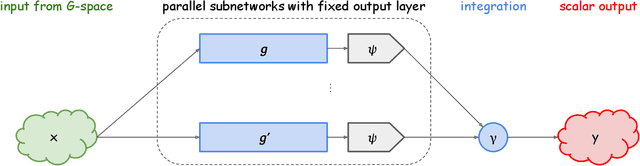
We identify hidden layers inside a DNN with group actions on the data space, and formulate the DNN as a dual voice transform with respect to Koopman operator, a linear representation of the group action. Based on the group theoretic arguments, particularly by using Schur's lemma, we show a simple proof of the universality of those DNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge