Why High-rank Neural Networks Generalize?: An Algebraic Framework with RKHSs

We derive a new Rademacher complexity bound for deep neural networks using Koopman operators, group representations, and reproducing kernel Hilbert spaces (RKHSs). The proposed bound describes why the models with high-rank weight matrices generalize well. Although there are existing bounds that attempt to describe this phenomenon, these existing bounds can be applied to limited types of models. We introduce an algebraic representation of neural networks and a kernel function to construct an RKHS to derive a bound for a wider range of realistic models. This work paves the way for the Koopman-based theory for Rademacher complexity bounds to be valid for more practical situations.

Generalization Through Growth: Hidden Dynamics Controls Depth Dependence

Recent theory has reduced the depth dependence of generalization bounds from exponential to polynomial and even depth-independent rates, yet these results remain tied to specific architectures and Euclidean inputs. We present a unified framework for arbitrary \blue{pseudo-metric} spaces in which a depth-\(k\) network is the composition of continuous hidden maps \(f:\mathcal{X}\to \mathcal{X}\) and an output map \(h:\mathcal{X}\to \mathbb{R}\). The resulting bound $O(\sqrt{(\alpha + \log \beta(k))/n})$ isolates the sole depth contribution in \(\beta(k)\), the word-ball growth of the semigroup generated by the hidden layers. By Gromov's theorem polynomial (resp. exponential) growth corresponds to virtually nilpotent (resp. expanding) dynamics, revealing a geometric dichotomy behind existing $O(\sqrt{k})$ (sublinear depth) and $\tilde{O}(1)$ (depth-independent) rates. We further provide covering-number estimates showing that expanding dynamics yield an exponential parameter saving via compositional expressivity. Our results decouple specification from implementation, offering architecture-agnostic and dynamical-systems-aware guarantees applicable to modern deep-learning paradigms such as test-time inference and diffusion models.

Lean Formalization of Generalization Error Bound by Rademacher Complexity

We formalize the generalization error bound using Rademacher complexity in the Lean 4 theorem prover. Generalization error quantifies the gap between a learning machine's performance on given training data versus unseen test data, and Rademacher complexity serves as an estimate of this error based on the complexity of learning machines, or hypothesis class. Unlike traditional methods such as PAC learning and VC dimension, Rademacher complexity is applicable across diverse machine learning scenarios including deep learning and kernel methods. We formalize key concepts and theorems, including the empirical and population Rademacher complexities, and establish generalization error bounds through formal proofs of McDiarmid's inequality, Hoeffding's lemma, and symmetrization arguments.

Constructive Universal Approximation Theorems for Deep Joint-Equivariant Networks by Schur's Lemma

We present a unified constructive universal approximation theorem covering a wide range of learning machines including both shallow and deep neural networks based on the group representation theory. Constructive here means that the distribution of parameters is given in a closed-form expression (called the ridgelet transform). Contrary to the case of shallow models, expressive power analysis of deep models has been conducted in a case-by-case manner. Recently, Sonoda et al. (2023a,b) developed a systematic method to show a constructive approximation theorem from scalar-valued joint-group-invariant feature maps, covering a formal deep network. However, each hidden layer was formalized as an abstract group action, so it was not possible to cover real deep networks defined by composites of nonlinear activation function. In this study, we extend the method for vector-valued joint-group-equivariant feature maps, so to cover such real networks.

A unified Fourier slice method to derive ridgelet transform for a variety of depth-2 neural networks

To investigate neural network parameters, it is easier to study the distribution of parameters than to study the parameters in each neuron. The ridgelet transform is a pseudo-inverse operator that maps a given function $f$ to the parameter distribution $\gamma$ so that a network $\mathtt{NN}[\gamma]$ reproduces $f$, i.e. $\mathtt{NN}[\gamma]=f$. For depth-2 fully-connected networks on a Euclidean space, the ridgelet transform has been discovered up to the closed-form expression, thus we could describe how the parameters are distributed. However, for a variety of modern neural network architectures, the closed-form expression has not been known. In this paper, we explain a systematic method using Fourier expressions to derive ridgelet transforms for a variety of modern networks such as networks on finite fields $\mathbb{F}_p$, group convolutional networks on abstract Hilbert space $\mathcal{H}$, fully-connected networks on noncompact symmetric spaces $G/K$, and pooling layers, or the $d$-plane ridgelet transform.

A Policy Gradient Primal-Dual Algorithm for Constrained MDPs with Uniform PAC Guarantees

We study a primal-dual reinforcement learning (RL) algorithm for the online constrained Markov decision processes (CMDP) problem, wherein the agent explores an optimal policy that maximizes return while satisfying constraints. Despite its widespread practical use, the existing theoretical literature on primal-dual RL algorithms for this problem only provides sublinear regret guarantees and fails to ensure convergence to optimal policies. In this paper, we introduce a novel policy gradient primal-dual algorithm with uniform probably approximate correctness (Uniform-PAC) guarantees, simultaneously ensuring convergence to optimal policies, sublinear regret, and polynomial sample complexity for any target accuracy. Notably, this represents the first Uniform-PAC algorithm for the online CMDP problem. In addition to the theoretical guarantees, we empirically demonstrate in a simple CMDP that our algorithm converges to optimal policies, while an existing algorithm exhibits oscillatory performance and constraint violation.

Joint Group Invariant Functions on Data-Parameter Domain Induce Universal Neural Networks

The symmetry and geometry of input data are considered to be encoded in the internal data representation inside the neural network, but the specific encoding rule has been less investigated. By focusing on a joint group invariant function on the data-parameter domain, we present a systematic rule to find a dual group action on the parameter domain from a group action on the data domain. Further, we introduce generalized neural networks induced from the joint invariant functions, and present a new group theoretic proof of their universality theorems by using Schur's lemma. Since traditional universality theorems were demonstrated based on functional analytical methods, this study sheds light on the group theoretic aspect of the approximation theory, connecting geometric deep learning to abstract harmonic analysis.

Deep Ridgelet Transform: Voice with Koopman Operator Proves Universality of Formal Deep Networks

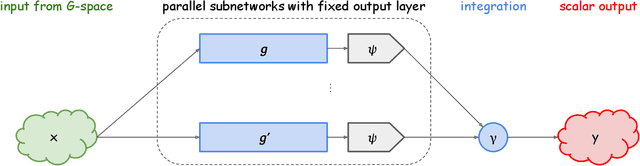
We identify hidden layers inside a DNN with group actions on the data space, and formulate the DNN as a dual voice transform with respect to Koopman operator, a linear representation of the group action. Based on the group theoretic arguments, particularly by using Schur's lemma, we show a simple proof of the universality of those DNNs.

LPML: LLM-Prompting Markup Language for Mathematical Reasoning

In utilizing large language models (LLMs) for mathematical reasoning, addressing the errors in the reasoning and calculation present in the generated text by LLMs is a crucial challenge. In this paper, we propose a novel framework that integrates the Chain-of-Thought (CoT) method with an external tool (Python REPL). We discovered that by prompting LLMs to generate structured text in XML-like markup language, we could seamlessly integrate CoT and the external tool and control the undesired behaviors of LLMs. With our approach, LLMs can utilize Python computation to rectify errors within CoT. We applied our method to ChatGPT (GPT-3.5) to solve challenging mathematical problems and demonstrated that combining CoT and Python REPL through the markup language enhances the reasoning capability of LLMs. Our approach enables LLMs to write the markup language and perform advanced mathematical reasoning using only zero-shot prompting.

Koopman-Based Bound for Generalization: New Aspect of Neural Networks Regarding Nonlinear Noise Filtering

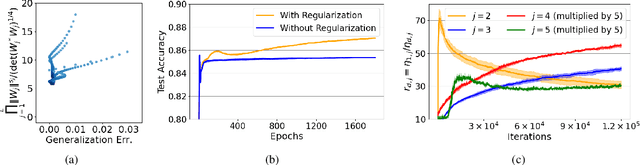
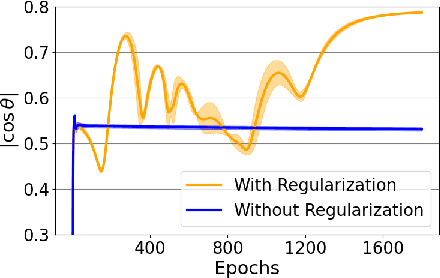
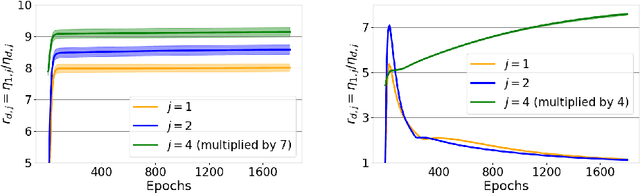
We propose a new bound for generalization of neural networks using Koopman operators. Unlike most of the existing works, we focus on the role of the final nonlinear transformation of the networks. Our bound is described by the reciprocal of the determinant of the weight matrices and is tighter than existing norm-based bounds when the weight matrices do not have small singular values. According to existing theories about the low-rankness of the weight matrices, it may be counter-intuitive that we focus on the case where singular values of weight matrices are not small. However, motivated by the final nonlinear transformation, we can see that our result sheds light on a new perspective regarding a noise filtering property of neural networks. Since our bound comes from Koopman operators, this work also provides a connection between operator-theoretic analysis and generalization of neural networks. Numerical results support the validity of our theoretical results.