Provably Transformers Harness Multi-Concept Word Semantics for Efficient In-Context Learning

Transformer-based large language models (LLMs) have displayed remarkable creative prowess and emergence capabilities. Existing empirical studies have revealed a strong connection between these LLMs' impressive emergence abilities and their in-context learning (ICL) capacity, allowing them to solve new tasks using only task-specific prompts without further fine-tuning. On the other hand, existing empirical and theoretical studies also show that there is a linear regularity of the multi-concept encoded semantic representation behind transformer-based LLMs. However, existing theoretical work fail to build up an understanding of the connection between this regularity and the innovative power of ICL. Additionally, prior work often focuses on simplified, unrealistic scenarios involving linear transformers or unrealistic loss functions, and they achieve only linear or sub-linear convergence rates. In contrast, this work provides a fine-grained mathematical analysis to show how transformers leverage the multi-concept semantics of words to enable powerful ICL and excellent out-of-distribution ICL abilities, offering insights into how transformers innovate solutions for certain unseen tasks encoded with multiple cross-concept semantics. Inspired by empirical studies on the linear latent geometry of LLMs, the analysis is based on a concept-based low-noise sparse coding prompt model. Leveraging advanced techniques, this work showcases the exponential 0-1 loss convergence over the highly non-convex training dynamics, which pioneeringly incorporates the challenges of softmax self-attention, ReLU-activated MLPs, and cross-entropy loss. Empirical simulations corroborate the theoretical findings.

Improved Particle Approximation Error for Mean Field Neural Networks

Mean-field Langevin dynamics (MFLD) minimizes an entropy-regularized nonlinear convex functional defined over the space of probability distributions. MFLD has gained attention due to its connection with noisy gradient descent for mean-field two-layer neural networks. Unlike standard Langevin dynamics, the nonlinearity of the objective functional induces particle interactions, necessitating multiple particles to approximate the dynamics in a finite-particle setting. Recent works (Chen et al., 2022; Suzuki et al., 2023b) have demonstrated the uniform-in-time propagation of chaos for MFLD, showing that the gap between the particle system and its mean-field limit uniformly shrinks over time as the number of particles increases. In this work, we improve the dependence on logarithmic Sobolev inequality (LSI) constants in their particle approximation errors, which can exponentially deteriorate with the regularization coefficient. Specifically, we establish an LSI-constant-free particle approximation error concerning the objective gap by leveraging the problem structure in risk minimization. As the application, we demonstrate improved convergence of MFLD, sampling guarantee for the mean-field stationary distribution, and uniform-in-time Wasserstein propagation of chaos in terms of particle complexity.

Convergence of mean-field Langevin dynamics: Time and space discretization, stochastic gradient, and variance reduction

The mean-field Langevin dynamics (MFLD) is a nonlinear generalization of the Langevin dynamics that incorporates a distribution-dependent drift, and it naturally arises from the optimization of two-layer neural networks via (noisy) gradient descent. Recent works have shown that MFLD globally minimizes an entropy-regularized convex functional in the space of measures. However, all prior analyses assumed the infinite-particle or continuous-time limit, and cannot handle stochastic gradient updates. We provide an general framework to prove a uniform-in-time propagation of chaos for MFLD that takes into account the errors due to finite-particle approximation, time-discretization, and stochastic gradient approximation. To demonstrate the wide applicability of this framework, we establish quantitative convergence rate guarantees to the regularized global optimal solution under (i) a wide range of learning problems such as neural network in the mean-field regime and MMD minimization, and (ii) different gradient estimators including SGD and SVRG. Despite the generality of our results, we achieve an improved convergence rate in both the SGD and SVRG settings when specialized to the standard Langevin dynamics.

Tight and fast generalization error bound of graph embedding in metric space

Recent studies have experimentally shown that we can achieve in non-Euclidean metric space effective and efficient graph embedding, which aims to obtain the vertices' representations reflecting the graph's structure in the metric space. Specifically, graph embedding in hyperbolic space has experimentally succeeded in embedding graphs with hierarchical-tree structure, e.g., data in natural languages, social networks, and knowledge bases. However, recent theoretical analyses have shown a much higher upper bound on non-Euclidean graph embedding's generalization error than Euclidean one's, where a high generalization error indicates that the incompleteness and noise in the data can significantly damage learning performance. It implies that the existing bound cannot guarantee the success of graph embedding in non-Euclidean metric space in a practical training data size, which can prevent non-Euclidean graph embedding's application in real problems. This paper provides a novel upper bound of graph embedding's generalization error by evaluating the local Rademacher complexity of the model as a function set of the distances of representation couples. Our bound clarifies that the performance of graph embedding in non-Euclidean metric space, including hyperbolic space, is better than the existing upper bounds suggest. Specifically, our new upper bound is polynomial in the metric space's geometric radius $R$ and can be $O(\frac{1}{S})$ at the fastest, where $S$ is the training data size. Our bound is significantly tighter and faster than the existing one, which can be exponential to $R$ and $O(\frac{1}{\sqrt{S}})$ at the fastest. Specific calculations on example cases show that graph embedding in non-Euclidean metric space can outperform that in Euclidean space with much smaller training data than the existing bound has suggested.

Primal and Dual Analysis of Entropic Fictitious Play for Finite-sum Problems

The entropic fictitious play (EFP) is a recently proposed algorithm that minimizes the sum of a convex functional and entropy in the space of measures -- such an objective naturally arises in the optimization of a two-layer neural network in the mean-field regime. In this work, we provide a concise primal-dual analysis of EFP in the setting where the learning problem exhibits a finite-sum structure. We establish quantitative global convergence guarantees for both the continuous-time and discrete-time dynamics based on properties of a proximal Gibbs measure introduced in Nitanda et al. (2022). Furthermore, our primal-dual framework entails a memory-efficient particle-based implementation of the EFP update, and also suggests a connection to gradient boosting methods. We illustrate the efficiency of our novel implementation in experiments including neural network optimization and image synthesis.

Parameter Averaging for SGD Stabilizes the Implicit Bias towards Flat Regions

Stochastic gradient descent is a workhorse for training deep neural networks due to its excellent generalization performance. Several studies demonstrated this success is attributed to the implicit bias of the method that prefers a flat minimum and developed new methods based on this perspective. Recently, Izmailov et al. (2018) empirically observed that an averaged stochastic gradient descent with a large step size can bring out the implicit bias more effectively and can converge more stably to a flat minimum than the vanilla stochastic gradient descent. In our work, we theoretically justify this observation by showing that the averaging scheme improves the bias-optimization tradeoff coming from the stochastic gradient noise: a large step size amplifies the bias but makes convergence unstable, and vice versa. Specifically, we show that the averaged stochastic gradient descent can get closer to a solution of a penalized objective on the sharpness than the vanilla stochastic gradient descent using the same step size under certain conditions. In experiments, we verify our theory and show this learning scheme significantly improves performance.

Koopman-Based Bound for Generalization: New Aspect of Neural Networks Regarding Nonlinear Noise Filtering

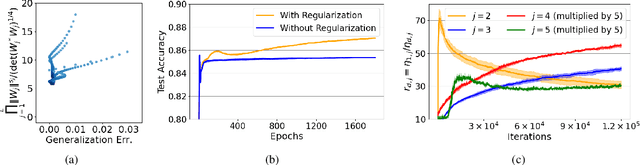
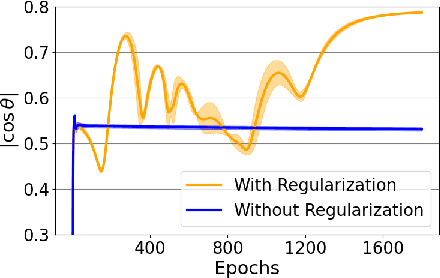
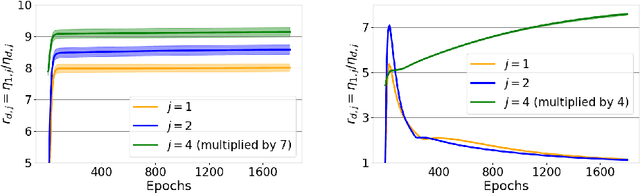
We propose a new bound for generalization of neural networks using Koopman operators. Unlike most of the existing works, we focus on the role of the final nonlinear transformation of the networks. Our bound is described by the reciprocal of the determinant of the weight matrices and is tighter than existing norm-based bounds when the weight matrices do not have small singular values. According to existing theories about the low-rankness of the weight matrices, it may be counter-intuitive that we focus on the case where singular values of weight matrices are not small. However, motivated by the final nonlinear transformation, we can see that our result sheds light on a new perspective regarding a noise filtering property of neural networks. Since our bound comes from Koopman operators, this work also provides a connection between operator-theoretic analysis and generalization of neural networks. Numerical results support the validity of our theoretical results.

Convex Analysis of the Mean Field Langevin Dynamics

As an example of the nonlinear Fokker-Planck equation, the mean field Langevin dynamics attracts attention due to its connection to (noisy) gradient descent on infinitely wide neural networks in the mean field regime, and hence the convergence property of the dynamics is of great theoretical interest. In this work, we give a simple and self-contained convergence rate analysis of the mean field Langevin dynamics with respect to the (regularized) objective function in both continuous and discrete time settings. The key ingredient of our proof is a proximal Gibbs distribution $p_q$ associated with the dynamics, which, in combination of techniques in [Vempala and Wibisono (2019)], allows us to develop a convergence theory parallel to classical results in convex optimization. Furthermore, we reveal that $p_q$ connects to the duality gap in the empirical risk minimization setting, which enables efficient empirical evaluation of the algorithm convergence.

Generalization Error Bound for Hyperbolic Ordinal Embedding

Hyperbolic ordinal embedding (HOE) represents entities as points in hyperbolic space so that they agree as well as possible with given constraints in the form of entity i is more similar to entity j than to entity k. It has been experimentally shown that HOE can obtain representations of hierarchical data such as a knowledge base and a citation network effectively, owing to hyperbolic space's exponential growth property. However, its theoretical analysis has been limited to ideal noiseless settings, and its generalization error in compensation for hyperbolic space's exponential representation ability has not been guaranteed. The difficulty is that existing generalization error bound derivations for ordinal embedding based on the Gramian matrix do not work in HOE, since hyperbolic space is not inner-product space. In this paper, through our novel characterization of HOE with decomposed Lorentz Gramian matrices, we provide a generalization error bound of HOE for the first time, which is at most exponential with respect to the embedding space's radius. Our comparison between the bounds of HOE and Euclidean ordinal embedding shows that HOE's generalization error is reasonable as a cost for its exponential representation ability.

BODAME: Bilevel Optimization for Defense Against Model Extraction

Model extraction attacks have become serious issues for service providers using machine learning. We consider an adversarial setting to prevent model extraction under the assumption that attackers will make their best guess on the service provider's model using query accesses, and propose to build a surrogate model that significantly keeps away the predictions of the attacker's model from those of the true model. We formulate the problem as a non-convex constrained bilevel optimization problem and show that for kernel models, it can be transformed into a non-convex 1-quadratically constrained quadratic program with a polynomial-time algorithm to find the global optimum. Moreover, we give a tractable transformation and an algorithm for more complicated models that are learned by using stochastic gradient descent-based algorithms. Numerical experiments show that the surrogate model performs well compared with existing defense models when the difference between the attacker's and service provider's distributions is large. We also empirically confirm the generalization ability of the surrogate model.