Uniform convergence of the smooth calibration error and its relationship with functional gradient

Calibration is a critical requirement for reliable probabilistic prediction, especially in high-risk applications. However, the theoretical understanding of which learning algorithms can simultaneously achieve high accuracy and good calibration remains limited, and many existing studies provide empirical validation or a theoretical guarantee in restrictive settings. To address this issue, in this work, we focus on the smooth calibration error (CE) and provide a uniform convergence bound, showing that the smooth CE is bounded by the sum of the smooth CE over the training dataset and a generalization gap. We further prove that the functional gradient of the loss function can effectively control the training smooth CE. Based on this framework, we analyze three representative algorithms: gradient boosting trees, kernel boosting, and two-layer neural networks. For each, we derive conditions under which both classification and calibration performances are simultaneously guaranteed. Our results offer new theoretical insights and practical guidance for designing reliable probabilistic models with provable calibration guarantees.

PAC-Bayes Analysis for Recalibration in Classification

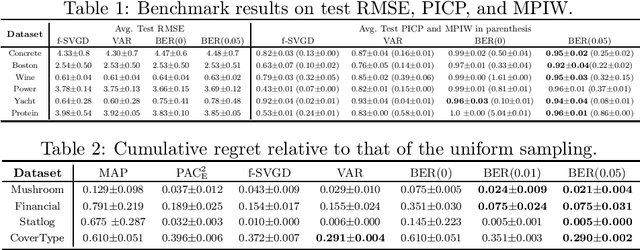
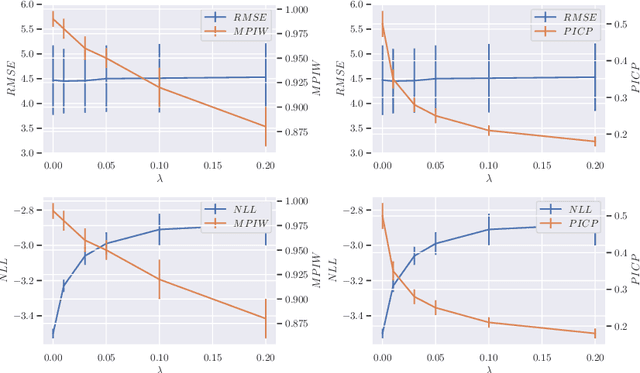
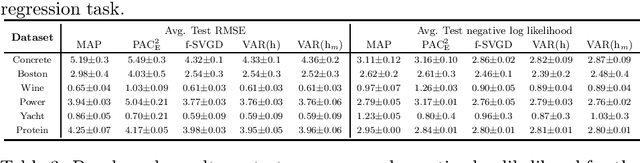
Nonparametric estimation with binning is widely employed in the calibration error evaluation and the recalibration of machine learning models. Recently, theoretical analyses of the bias induced by this estimation approach have been actively pursued; however, the understanding of the generalization of the calibration error to unknown data remains limited. In addition, although many recalibration algorithms have been proposed, their generalization performance lacks theoretical guarantees. To address this problem, we conduct a generalization analysis of the calibration error under the probably approximately correct (PAC) Bayes framework. This approach enables us to derive a first optimizable upper bound for the generalization error in the calibration context. We then propose a generalization-aware recalibration algorithm based on our generalization theory. Numerical experiments show that our algorithm improves the Gaussian-process-based recalibration performance on various benchmark datasets and models.

Time-Independent Information-Theoretic Generalization Bounds for SGLD

We provide novel information-theoretic generalization bounds for stochastic gradient Langevin dynamics (SGLD) under the assumptions of smoothness and dissipativity, which are widely used in sampling and non-convex optimization studies. Our bounds are time-independent and decay to zero as the sample size increases, regardless of the number of iterations and whether the step size is fixed. Unlike previous studies, we derive the generalization error bounds by focusing on the time evolution of the Kullback--Leibler divergence, which is related to the stability of datasets and is the upper bound of the mutual information between output parameters and an input dataset. Additionally, we establish the first information-theoretic generalization bound when the training and test loss are the same by showing that a loss function of SGLD is sub-exponential. This bound is also time-independent and removes the problematic step size dependence in existing work, leading to an improved excess risk bound by combining our analysis with the existing non-convex optimization error bounds.

Information-theoretic Analysis of Test Data Sensitivity in Uncertainty

Bayesian inference is often utilized for uncertainty quantification tasks. A recent analysis by Xu and Raginsky 2022 rigorously decomposed the predictive uncertainty in Bayesian inference into two uncertainties, called aleatoric and epistemic uncertainties, which represent the inherent randomness in the data-generating process and the variability due to insufficient data, respectively. They analyzed those uncertainties in an information-theoretic way, assuming that the model is well-specified and treating the model's parameters as latent variables. However, the existing information-theoretic analysis of uncertainty cannot explain the widely believed property of uncertainty, known as the sensitivity between the test and training data. It implies that when test data are similar to training data in some sense, the epistemic uncertainty should become small. In this work, we study such uncertainty sensitivity using our novel decomposition method for the predictive uncertainty. Our analysis successfully defines such sensitivity using information-theoretic quantities. Furthermore, we extend the existing analysis of Bayesian meta-learning and show the novel sensitivities among tasks for the first time.

Excess risk analysis for epistemic uncertainty with application to variational inference

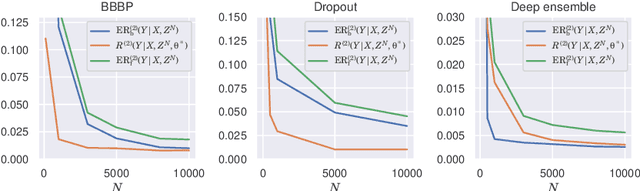
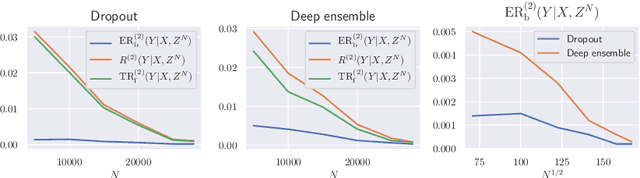
We analyze the epistemic uncertainty (EU) of supervised learning in Bayesian inference by focusing on the excess risk. Existing analysis is limited to the Bayesian setting, which assumes a correct model and exact Bayesian posterior distribution. Thus we cannot apply the existing theory to modern Bayesian algorithms, such as variational inference. To address this, we present a novel EU analysis in the frequentist setting, where data is generated from an unknown distribution. We show a relation between the generalization ability and the widely used EU measurements, such as the variance and entropy of the predictive distribution. Then we show their convergence behaviors theoretically. Finally, we propose new variational inference that directly controls the prediction and EU evaluation performances based on the PAC-Bayesian theory. Numerical experiments show that our algorithm significantly improves the EU evaluation over the existing methods.

Loss function based second-order Jensen inequality and its application to particle variational inference

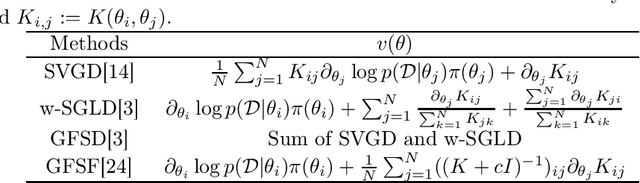
Bayesian model averaging, obtained as the expectation of a likelihood function by a posterior distribution, has been widely used for prediction, evaluation of uncertainty, and model selection. Various approaches have been developed to efficiently capture the information in the posterior distribution; one such approach is the optimization of a set of models simultaneously with interaction to ensure the diversity of the individual models in the same way as ensemble learning. A representative approach is particle variational inference (PVI), which uses an ensemble of models as an empirical approximation for the posterior distribution. PVI iteratively updates each model with a repulsion force to ensure the diversity of the optimized models. However, despite its promising performance, a theoretical understanding of this repulsion and its association with the generalization ability remains unclear. In this paper, we tackle this problem in light of PAC-Bayesian analysis. First, we provide a new second-order Jensen inequality, which has the repulsion term based on the loss function. Thanks to the repulsion term, it is tighter than the standard Jensen inequality. Then, we derive a novel generalization error bound and show that it can be reduced by enhancing the diversity of models. Finally, we derive a new PVI that optimizes the generalization error bound directly. Numerical experiments demonstrate that the performance of the proposed PVI compares favorably with existing methods in the experiment.

Time-varying Gaussian Process Bandit Optimization with Non-constant Evaluation Time

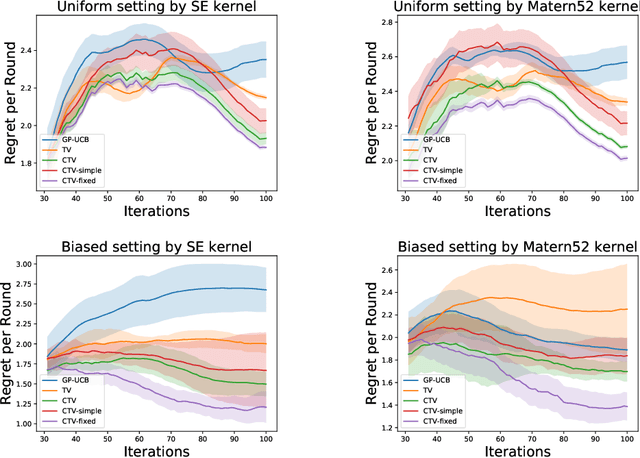
The Gaussian process bandit is a problem in which we want to find a maximizer of a black-box function with the minimum number of function evaluations. If the black-box function varies with time, then time-varying Bayesian optimization is a promising framework. However, a drawback with current methods is in the assumption that the evaluation time for every observation is constant, which can be unrealistic for many practical applications, e.g., recommender systems and environmental monitoring. As a result, the performance of current methods can be degraded when this assumption is violated. To cope with this problem, we propose a novel time-varying Bayesian optimization algorithm that can effectively handle the non-constant evaluation time. Furthermore, we theoretically establish a regret bound of our algorithm. Our bound elucidates that a pattern of the evaluation time sequence can hugely affect the difficulty of the problem. We also provide experimental results to validate the practical effectiveness of the proposed method.

Frank-Wolfe Stein Sampling

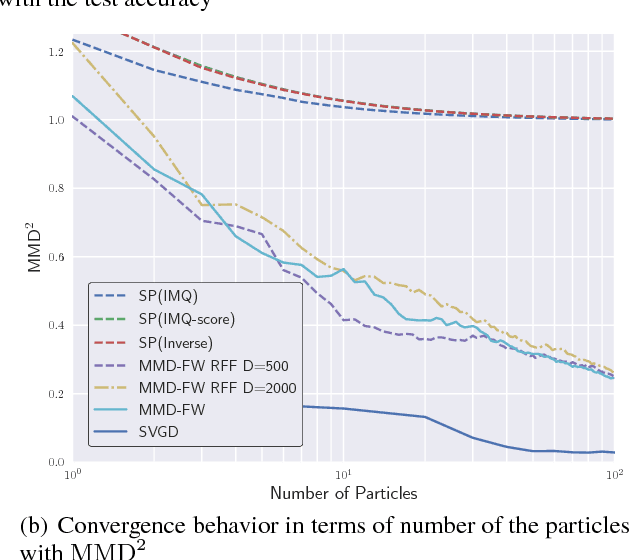
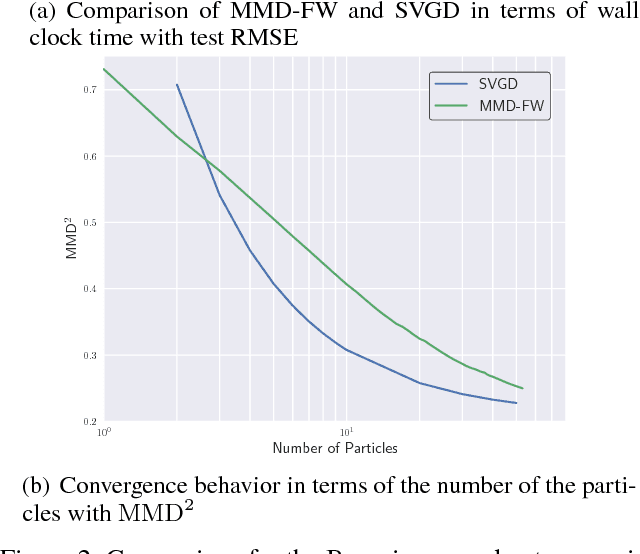
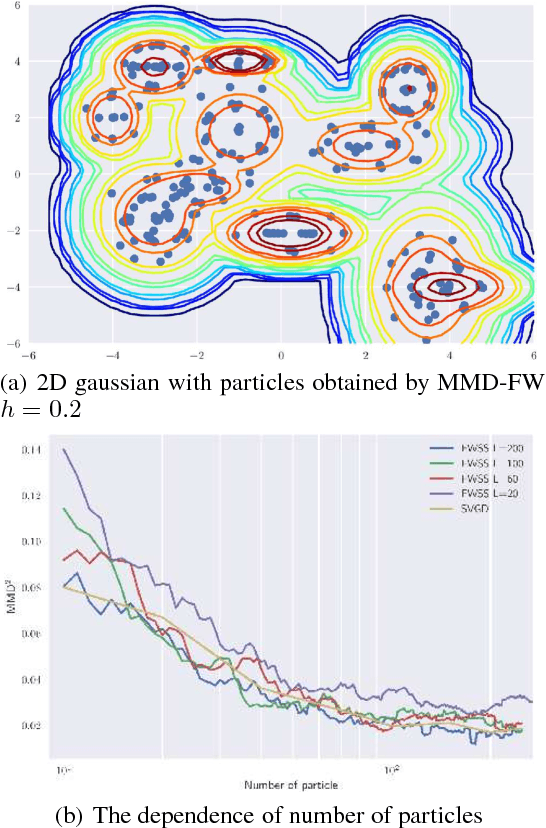
In Bayesian inference, the posterior distributions are difficult to obtain analytically for complex models such as neural networks. Variational inference usually uses a parametric distribution to approximate, from which we can easily draw samples. Recently discrete approximation by particles has attracted attention because of its expressive ability. An example is Stein variational gradient descent (SVGD), which iteratively optimizes particles. Although SVGD has been shown to be computationally efficient empirically, its theoretical properties have not been clarified yet and no finite sample bound of a convergence rate is known. Another example is Stein points (SP), which minimizes kernelized Stein discrepancy directly. The finite sample bound of SP is $\mathcal{O}(\sqrt{\log{N}/N})$ for $N$ particles, which is computationally inefficient empirically, especially in high-dimensional problems. In this paper, we propose a novel method named \emph{Frank-Wolfe Stein sampling}, which minimizes the maximum mean discrepancy in a greedy way. Our method is computationally efficient empirically and theoretically achieves a faster convergence rate, $\mathcal{O}(e^{-N})$. Numerical experiments show the superiority of our method.

Variational Inference based on Robust Divergences

Robustness to outliers is a central issue in real-world machine learning applications. While replacing a model to a heavy-tailed one (e.g., from Gaussian to Student-t) is a standard approach for robustification, it can only be applied to simple models. In this paper, based on Zellner's optimization and variational formulation of Bayesian inference, we propose an outlier-robust pseudo-Bayesian variational method by replacing the Kullback-Leibler divergence used for data fitting to a robust divergence such as the beta- and gamma-divergences. An advantage of our approach is that superior but complex models such as deep networks can also be handled. We theoretically prove that, for deep networks with ReLU activation functions, the \emph{influence function} in our proposed method is bounded, while it is unbounded in the ordinary variational inference. This implies that our proposed method is robust to both of input and output outliers, while the ordinary variational method is not. We experimentally demonstrate that our robust variational method outperforms ordinary variational inference in regression and classification with deep networks.

Expectation Propagation for t-Exponential Family Using Q-Algebra

Exponential family distributions are highly useful in machine learning since their calculation can be performed efficiently through natural parameters. The exponential family has recently been extended to the t-exponential family, which contains Student-t distributions as family members and thus allows us to handle noisy data well. However, since the t-exponential family is denied by the deformed exponential, we cannot derive an efficient learning algorithm for the t-exponential family such as expectation propagation (EP). In this paper, we borrow the mathematical tools of q-algebra from statistical physics and show that the pseudo additivity of distributions allows us to perform calculation of t-exponential family distributions through natural parameters. We then develop an expectation propagation (EP) algorithm for the t-exponential family, which provides a deterministic approximation to the posterior or predictive distribution with simple moment matching. We finally apply the proposed EP algorithm to the Bayes point machine and Student-t process classication, and demonstrate their performance numerically.