Classification with Rejection Based on Cost-sensitive Classification

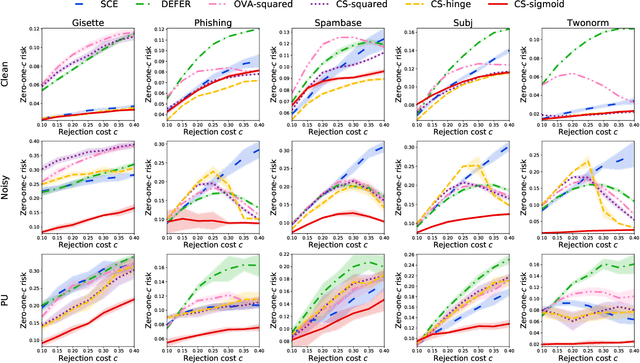
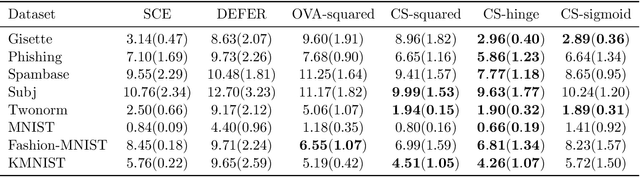
The goal of classification with rejection is to avoid risky misclassification in error-critical applications such as medical diagnosis and product inspection. In this paper, based on the relationship between classification with rejection and cost-sensitive classification, we propose a novel method of classification with rejection by learning an ensemble of cost-sensitive classifiers, which satisfies all the following properties for the first time: (i) it can avoid estimating class-posterior probabilities, resulting in improved classification accuracy. (ii) it allows a flexible choice of losses including non-convex ones, (iii) it does not require complicated modifications when using different losses, (iv) it is applicable to both binary and multiclass cases, and (v) it is theoretically justifiable for any classification-calibrated loss. Experimental results demonstrate the usefulness of our proposed approach in clean-labeled, noisy-labeled, and positive-unlabeled classification.

ATRO: Adversarial Training with a Rejection Option

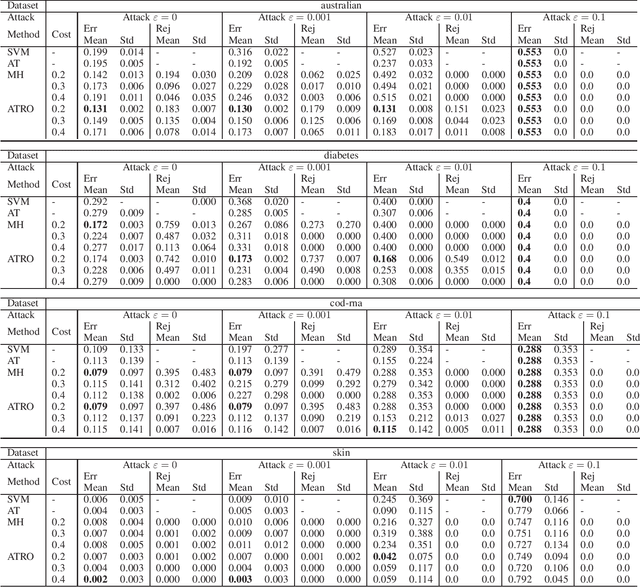
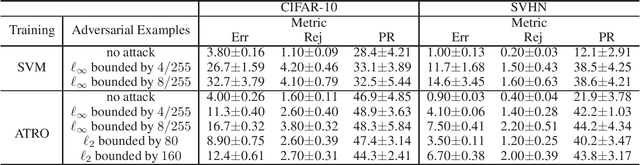
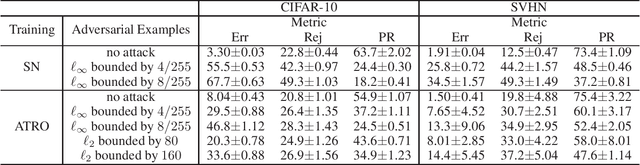
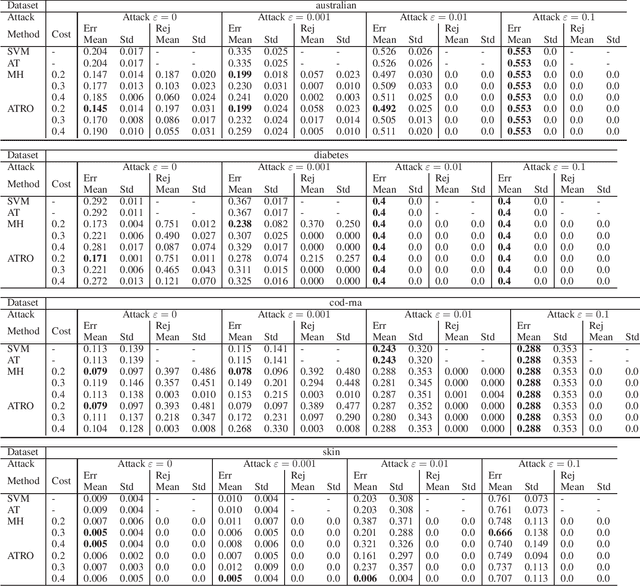
This paper proposes a classification framework with a rejection option to mitigate the performance deterioration caused by adversarial examples. While recent machine learning algorithms achieve high prediction performance, they are empirically vulnerable to adversarial examples, which are slightly perturbed data samples that are wrongly classified. In real-world applications, adversarial attacks using such adversarial examples could cause serious problems. To this end, various methods are proposed to obtain a classifier that is robust against adversarial examples. Adversarial training is one of them, which trains a classifier to minimize the worst-case loss under adversarial attacks. In this paper, in order to acquire a more reliable classifier against adversarial attacks, we propose the method of Adversarial Training with a Rejection Option (ATRO). Applying the adversarial training objective to both a classifier and a rejection function simultaneously, classifiers trained by ATRO can choose to abstain from classification when it has insufficient confidence to classify a test data point. We examine the feasibility of the framework using the surrogate maximum hinge loss and establish a generalization bound for linear models. Furthermore, we empirically confirmed the effectiveness of ATRO using various models and real-world datasets.

Classification from Ambiguity Comparisons

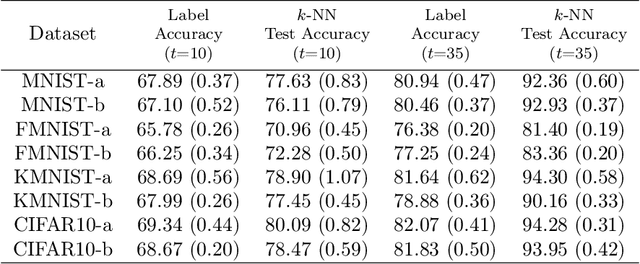
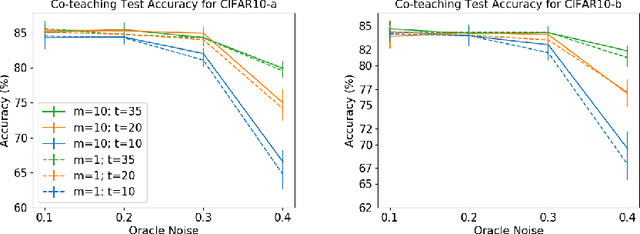
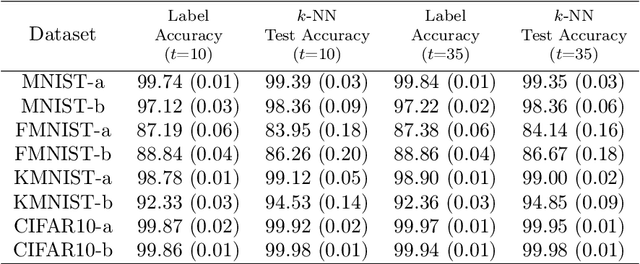
Labeling data is an unavoidable pre-processing procedure for most machine learning tasks. However, it takes a considerable amount of time, money, and labor to collect accurate \textit{explicit class labels} for a large dataset. A positivity comparison oracle has been adapted to relieve this burden, where two data points are received as input and the oracle answers which one is more likely to be positive. However, when information about the classification threshold is lacking, this oracle alone can at most rank all data points on the basis of their relative positivity; thus, it still needs to access explicit class labels. In order to harness pairwise comparisons in a more effective way, we propose an \textit{ambiguity comparison oracle}. This oracle also receives two data points as input, and it answers which one is more ambiguous, or more difficult to assign a label to. We then propose an efficient adaptive labeling algorithm that can actively query \textit{only pairwise comparison oracles} without accessing the explicit labeling oracle. We also address the situation where the labeling budget is insufficient compared to the dataset size, which can be dealt with by plugging the proposed algorithm into an active learning algorithm. Furthermore, we confirm the feasibility of the proposed oracle and the performance of the proposed labeling algorithms theoretically and empirically.

Classification from Triplet Comparison Data

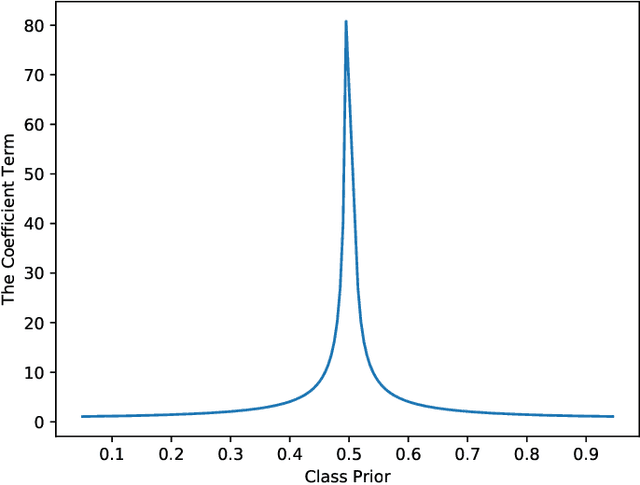
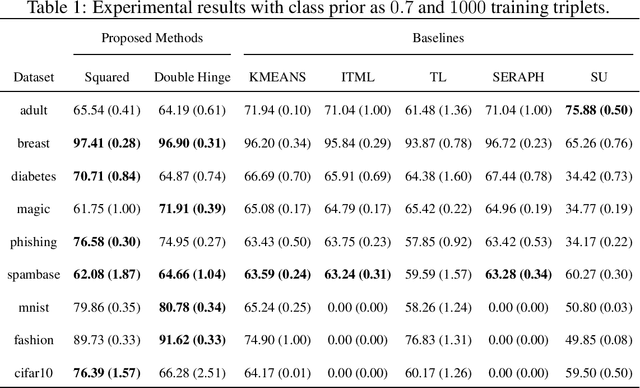
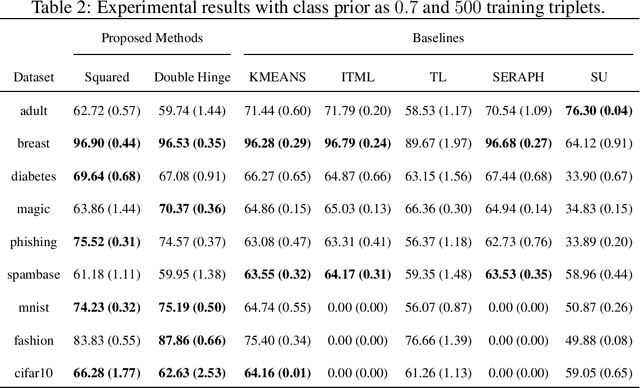
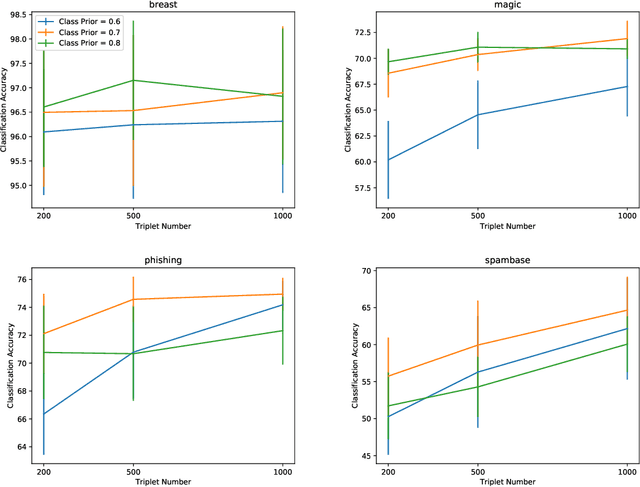
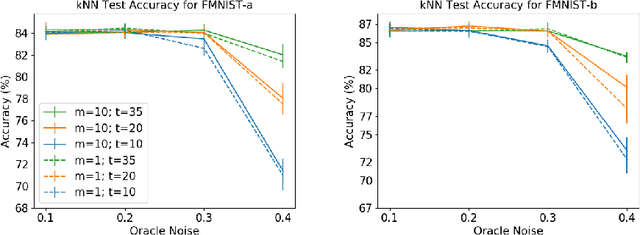
Learning from triplet comparison data has been extensively studied in the context of metric learning, where we want to learn a distance metric between two instances, and ordinal embedding, where we want to learn an embedding in an Euclidean space of the given instances that preserves the comparison order as well as possible. Unlike fully-labeled data, triplet comparison data can be collected in a more accurate and human-friendly way. Although learning from triplet comparison data has been considered in many applications, an important fundamental question of whether we can learn a classifier only from triplet comparison data has remained unanswered. In this paper, we give a positive answer to this important question by proposing an unbiased estimator for the classification risk under the empirical risk minimization framework. Since the proposed method is based on the empirical risk minimization framework, it inherently has the advantage that any surrogate loss function and any model, including neural networks, can be easily applied. Furthermore, we theoretically establish an estimation error bound for the proposed empirical risk minimizer. Finally, we provide experimental results to show that our method empirically works well and outperforms various baseline methods.

Frank-Wolfe Stein Sampling

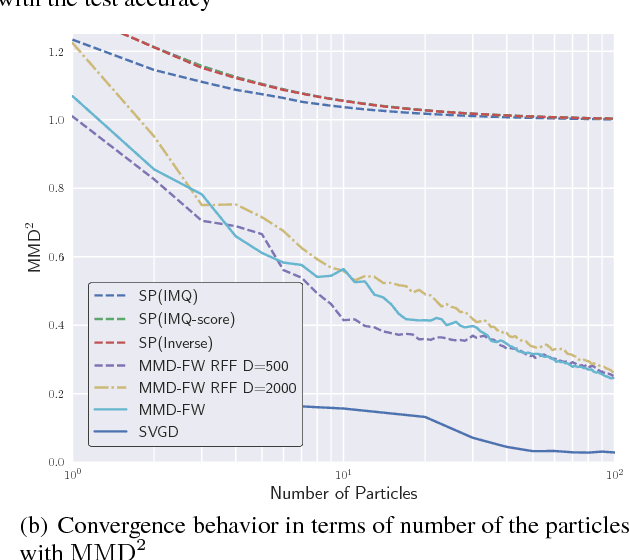
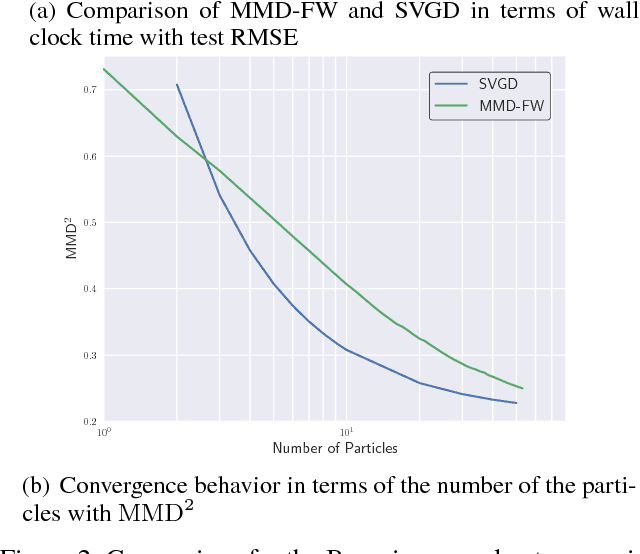
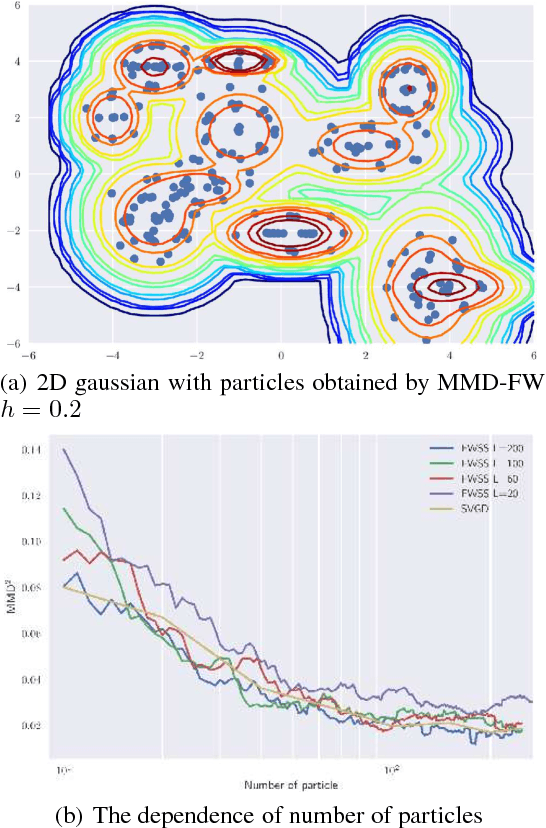
In Bayesian inference, the posterior distributions are difficult to obtain analytically for complex models such as neural networks. Variational inference usually uses a parametric distribution to approximate, from which we can easily draw samples. Recently discrete approximation by particles has attracted attention because of its expressive ability. An example is Stein variational gradient descent (SVGD), which iteratively optimizes particles. Although SVGD has been shown to be computationally efficient empirically, its theoretical properties have not been clarified yet and no finite sample bound of a convergence rate is known. Another example is Stein points (SP), which minimizes kernelized Stein discrepancy directly. The finite sample bound of SP is $\mathcal{O}(\sqrt{\log{N}/N})$ for $N$ particles, which is computationally inefficient empirically, especially in high-dimensional problems. In this paper, we propose a novel method named \emph{Frank-Wolfe Stein sampling}, which minimizes the maximum mean discrepancy in a greedy way. Our method is computationally efficient empirically and theoretically achieves a faster convergence rate, $\mathcal{O}(e^{-N})$. Numerical experiments show the superiority of our method.

Stochastic Divergence Minimization for Biterm Topic Model

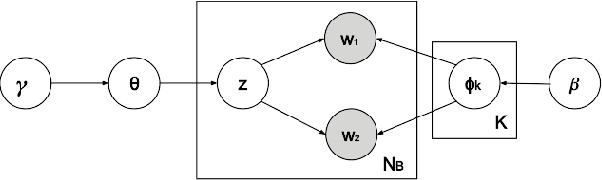
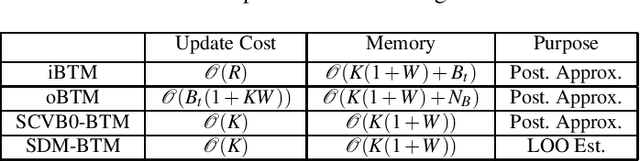
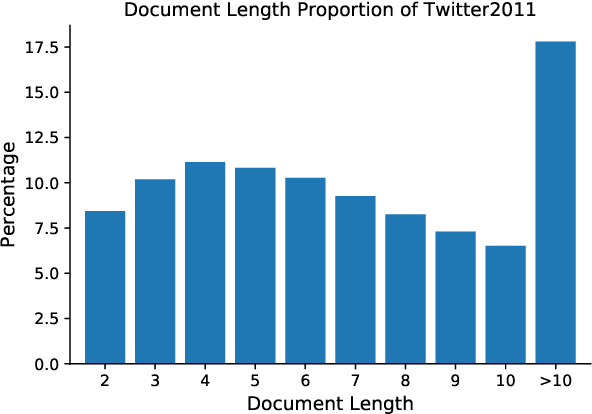
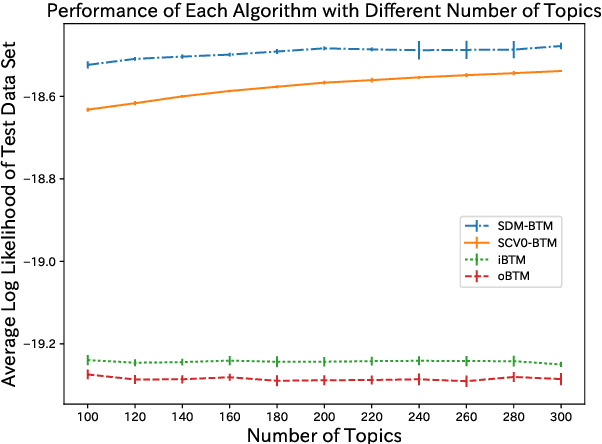
As the emergence and the thriving development of social networks, a huge number of short texts are accumulated and need to be processed. Inferring latent topics of collected short texts is useful for understanding its hidden structure and predicting new contents. Unlike conventional topic models such as latent Dirichlet allocation (LDA), a biterm topic model (BTM) was recently proposed for short texts to overcome the sparseness of document-level word co-occurrences by directly modeling the generation process of word pairs. Stochastic inference algorithms based on collapsed Gibbs sampling (CGS) and collapsed variational inference have been proposed for BTM. However, they either require large computational complexity, or rely on very crude estimation. In this work, we develop a stochastic divergence minimization inference algorithm for BTM to estimate latent topics more accurately in a scalable way. Experiments demonstrate the superiority of our proposed algorithm compared with existing inference algorithms.