Strategic Learning with Local Explanations as Feedback

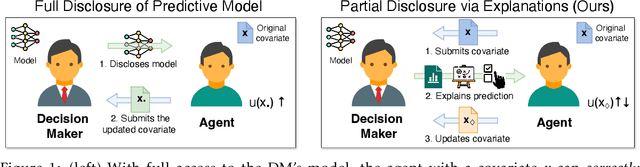
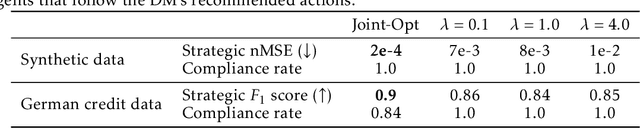
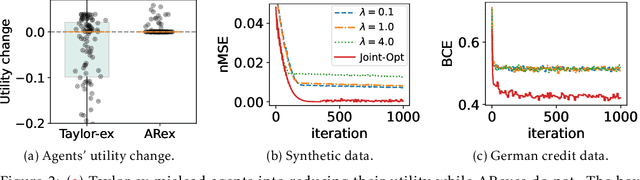
We investigate algorithmic decision problems where agents can respond strategically to the decision maker's (DM) models. The demand for clear and actionable explanations from DMs to (potentially strategic) agents continues to rise. While prior work often treats explanations as full model disclosures, explanations in practice might convey only partial information, which can lead to misinterpretations and harmful responses. When full disclosure of the predictive model is neither feasible nor desirable, a key open question is how DMs can use explanations to maximise their utility without compromising agent welfare. In this work, we explore well-known local and global explanation methods, and establish a necessary condition to prevent explanations from misleading agents into self-harming actions. Moreover, with conditional homogeneity, we establish that action recommendation (AR)-based explanations are sufficient for non-harmful responses, akin to the revelation principle in information design. To operationalise AR-based explanations, we propose a simple algorithm to jointly optimise the predictive model and AR policy to balance DM outcomes with agent welfare. Our empirical results demonstrate the benefits of this approach as a more refined strategy for safe and effective partial model disclosure in algorithmic decision-making.

PUATE: Semiparametric Efficient Average Treatment Effect Estimation from Treated (Positive) and Unlabeled Units

The estimation of average treatment effects (ATEs), defined as the difference in expected outcomes between treatment and control groups, is a central topic in causal inference. This study develops semiparametric efficient estimators for ATE estimation in a setting where only a treatment group and an unknown group-comprising units for which it is unclear whether they received the treatment or control-are observable. This scenario represents a variant of learning from positive and unlabeled data (PU learning) and can be regarded as a special case of ATE estimation with missing data. For this setting, we derive semiparametric efficiency bounds, which provide lower bounds on the asymptotic variance of regular estimators. We then propose semiparametric efficient ATE estimators whose asymptotic variance aligns with these efficiency bounds. Our findings contribute to causal inference with missing data and weakly supervised learning.

Debiased Nonparametric Regression for Statistical Inference and Distributionally Robustness

This study proposes a debiasing method for smooth nonparametric estimators. While machine learning techniques such as random forests and neural networks have demonstrated strong predictive performance, their theoretical properties remain relatively underexplored. Specifically, many modern algorithms lack assurances of pointwise asymptotic normality and uniform convergence, which are critical for statistical inference and robustness under covariate shift and have been well-established for classical methods like Nadaraya-Watson regression. To address this, we introduce a model-free debiasing method that guarantees these properties for smooth estimators derived from any nonparametric regression approach. By adding a correction term that estimates the conditional expected residual of the original estimator, or equivalently, its estimation error, we obtain a debiased estimator with proven pointwise asymptotic normality, uniform convergence, and Gaussian process approximation. These properties enable statistical inference and enhance robustness to covariate shift, making the method broadly applicable to a wide range of nonparametric regression problems.

Minimax Optimal Simple Regret in Two-Armed Best-Arm Identification

This study investigates an asymptotically minimax optimal algorithm in the two-armed fixed-budget best-arm identification (BAI) problem. Given two treatment arms, the objective is to identify the arm with the highest expected outcome through an adaptive experiment. We focus on the Neyman allocation, where treatment arms are allocated following the ratio of their outcome standard deviations. Our primary contribution is to prove the minimax optimality of the Neyman allocation for the simple regret, defined as the difference between the expected outcomes of the true best arm and the estimated best arm. Specifically, we first derive a minimax lower bound for the expected simple regret, which characterizes the worst-case performance achievable under the location-shift distributions, including Gaussian distributions. We then show that the simple regret of the Neyman allocation asymptotically matches this lower bound, including the constant term, not just the rate in terms of the sample size, under the worst-case distribution. Notably, our optimality result holds without imposing locality restrictions on the distribution, such as the local asymptotic normality. Furthermore, we demonstrate that the Neyman allocation reduces to the uniform allocation, i.e., the standard randomized controlled trial, under Bernoulli distributions.

Debiased Regression for Root-N-Consistent Conditional Mean Estimation

This study introduces a debiasing method for regression estimators, including high-dimensional and nonparametric regression estimators. For example, nonparametric regression methods allow for the estimation of regression functions in a data-driven manner with minimal assumptions; however, these methods typically fail to achieve $\sqrt{n}$-consistency in their convergence rates, and many, including those in machine learning, lack guarantees that their estimators asymptotically follow a normal distribution. To address these challenges, we propose a debiasing technique for nonparametric estimators by adding a bias-correction term to the original estimators, extending the conventional one-step estimator used in semiparametric analysis. Specifically, for each data point, we estimate the conditional expected residual of the original nonparametric estimator, which can, for instance, be computed using kernel (Nadaraya-Watson) regression, and incorporate it as a bias-reduction term. Our theoretical analysis demonstrates that the proposed estimator achieves $\sqrt{n}$-consistency and asymptotic normality under a mild convergence rate condition for both the original nonparametric estimator and the conditional expected residual estimator. Notably, this approach remains model-free as long as the original estimator and the conditional expected residual estimator satisfy the convergence rate condition. The proposed method offers several advantages, including improved estimation accuracy and simplified construction of confidence intervals.

Doubly Robust Regression Discontinuity Designs

This study introduces a doubly robust (DR) estimator for regression discontinuity (RD) designs. In RD designs, treatment effects are estimated in a quasi-experimental setting where treatment assignment depends on whether a running variable surpasses a predefined cutoff. A common approach in RD estimation is to apply nonparametric regression methods, such as local linear regression. In such an approach, the validity relies heavily on the consistency of nonparametric estimators and is limited by the nonparametric convergence rate, thereby preventing $\sqrt{n}$-consistency. To address these issues, we propose the DR-RD estimator, which combines two distinct estimators for the conditional expected outcomes. If either of these estimators is consistent, the treatment effect estimator remains consistent. Furthermore, due to the debiasing effect, our proposed estimator achieves $\sqrt{n}$-consistency if both regression estimators satisfy certain mild conditions, which also simplifies statistical inference.

Conformal Predictive Portfolio Selection

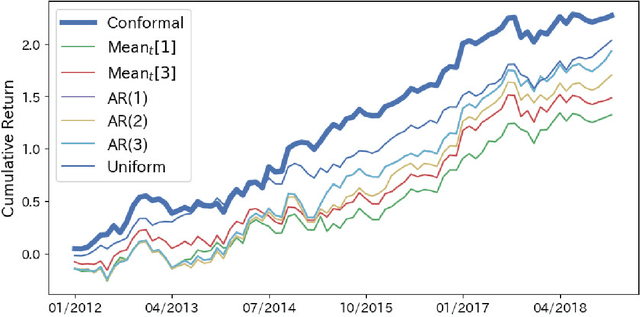
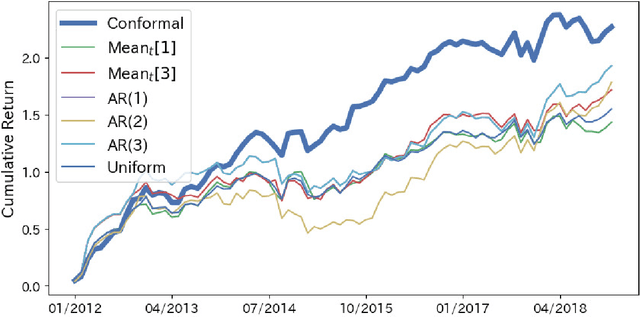
This study explores portfolio selection using predictive models for portfolio returns. Portfolio selection is a fundamental task in finance, and various methods have been developed to achieve this goal. For example, the mean-variance approach constructs portfolios by balancing the trade-off between the mean and variance of asset returns, while the quantile-based approach optimizes portfolios by accounting for tail risk. These traditional methods often rely on distributional information estimated from historical data. However, a key concern is the uncertainty of future portfolio returns, which may not be fully captured by simple reliance on historical data, such as using the sample average. To address this, we propose a framework for predictive portfolio selection using conformal inference, called Conformal Predictive Portfolio Selection (CPPS). Our approach predicts future portfolio returns, computes corresponding prediction intervals, and selects the desirable portfolio based on these intervals. The framework is flexible and can accommodate a variety of predictive models, including autoregressive (AR) models, random forests, and neural networks. We demonstrate the effectiveness of our CPPS framework using an AR model and validate its performance through empirical studies, showing that it provides superior returns compared to simpler strategies.

Adaptive Generalized Neyman Allocation: Local Asymptotic Minimax Optimal Best Arm Identification

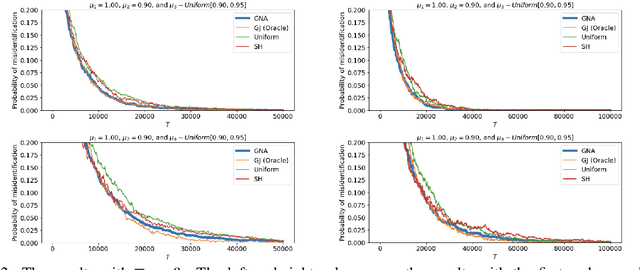
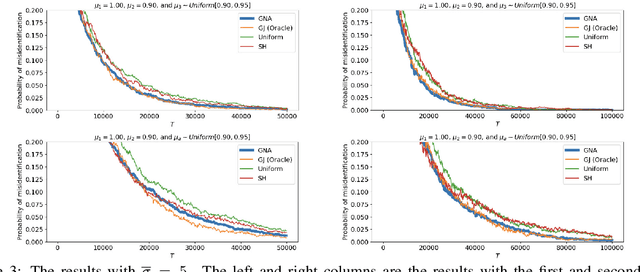
This study investigates a local asymptotic minimax optimal strategy for fixed-budget best arm identification (BAI). We propose the Adaptive Generalized Neyman Allocation (AGNA) strategy and show that its worst-case upper bound of the probability of misidentifying the best arm aligns with the worst-case lower bound under the small-gap regime, where the gap between the expected outcomes of the best and suboptimal arms is small. Our strategy corresponds to a generalization of the Neyman allocation for two-armed bandits (Neyman, 1934; Kaufmann et al., 2016) and a refinement of existing strategies such as the ones proposed by Glynn & Juneja (2004) and Shin et al. (2018). Compared to Komiyama et al. (2022), which proposes a minimax rate-optimal strategy, our proposed strategy has a tighter upper bound that exactly matches the lower bound, including the constant terms, by restricting the class of distributions to the class of small-gap distributions. Our result contributes to the longstanding open issue about the existence of asymptotically optimal strategies in fixed-budget BAI, by presenting the local asymptotic minimax optimal strategy.

Active Adaptive Experimental Design for Treatment Effect Estimation with Covariate Choices

This study designs an adaptive experiment for efficiently estimating average treatment effect (ATEs). We consider an adaptive experiment where an experimenter sequentially samples an experimental unit from a covariate density decided by the experimenter and assigns a treatment. After assigning a treatment, the experimenter observes the corresponding outcome immediately. At the end of the experiment, the experimenter estimates an ATE using gathered samples. The objective of the experimenter is to estimate the ATE with a smaller asymptotic variance. Existing studies have designed experiments that adaptively optimize the propensity score (treatment-assignment probability). As a generalization of such an approach, we propose a framework under which an experimenter optimizes the covariate density, as well as the propensity score, and find that optimizing both covariate density and propensity score reduces the asymptotic variance more than optimizing only the propensity score. Based on this idea, in each round of our experiment, the experimenter optimizes the covariate density and propensity score based on past observations. To design an adaptive experiment, we first derive the efficient covariate density and propensity score that minimizes the semiparametric efficiency bound, a lower bound for the asymptotic variance given a fixed covariate density and a fixed propensity score. Next, we design an adaptive experiment using the efficient covariate density and propensity score sequentially estimated during the experiment. Lastly, we propose an ATE estimator whose asymptotic variance aligns with the minimized semiparametric efficiency bound.

Triple/Debiased Lasso for Statistical Inference of Conditional Average Treatment Effects

This study investigates the estimation and the statistical inference about Conditional Average Treatment Effects (CATEs), which have garnered attention as a metric representing individualized causal effects. In our data-generating process, we assume linear models for the outcomes associated with binary treatments and define the CATE as a difference between the expected outcomes of these linear models. This study allows the linear models to be high-dimensional, and our interest lies in consistent estimation and statistical inference for the CATE. In high-dimensional linear regression, one typical approach is to assume sparsity. However, in our study, we do not assume sparsity directly. Instead, we consider sparsity only in the difference of the linear models. We first use a doubly robust estimator to approximate this difference and then regress the difference on covariates with Lasso regularization. Although this regression estimator is consistent for the CATE, we further reduce the bias using the techniques in double/debiased machine learning (DML) and debiased Lasso, leading to $\sqrt{n}$-consistency and confidence intervals. We refer to the debiased estimator as the triple/debiased Lasso (TDL), applying both DML and debiased Lasso techniques. We confirm the soundness of our proposed method through simulation studies.