Frank-Wolfe Stein Sampling

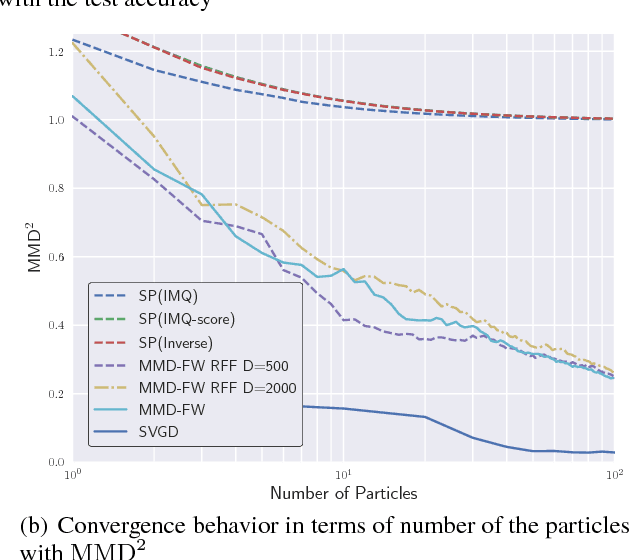
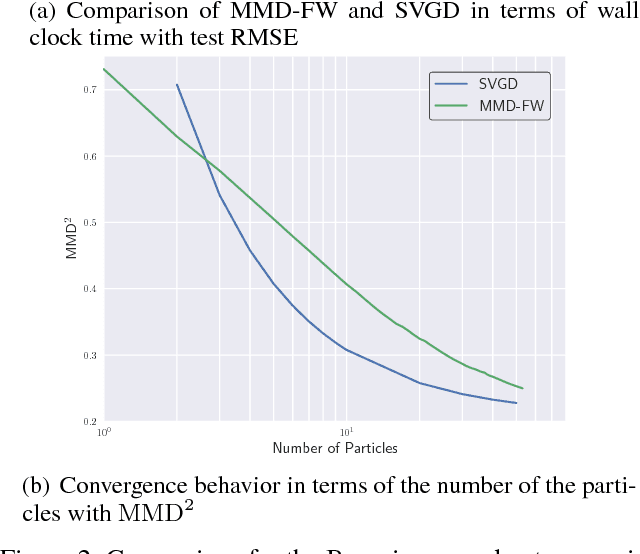
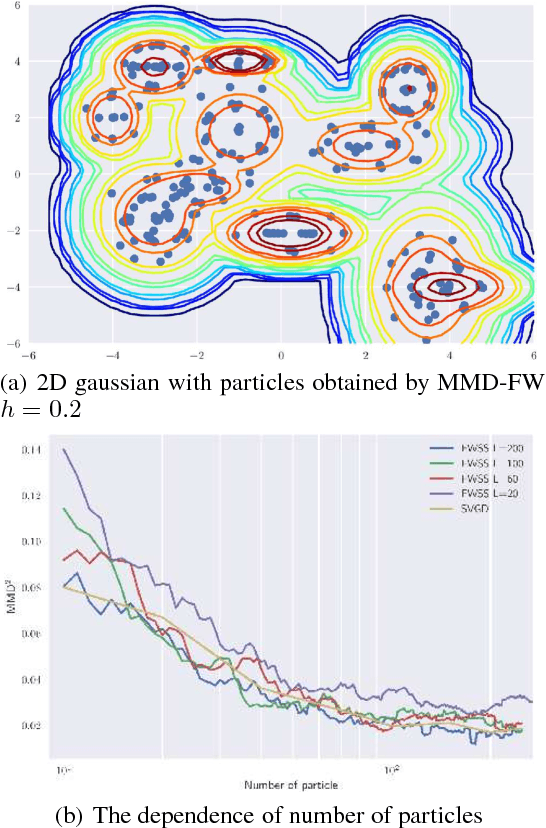
In Bayesian inference, the posterior distributions are difficult to obtain analytically for complex models such as neural networks. Variational inference usually uses a parametric distribution to approximate, from which we can easily draw samples. Recently discrete approximation by particles has attracted attention because of its expressive ability. An example is Stein variational gradient descent (SVGD), which iteratively optimizes particles. Although SVGD has been shown to be computationally efficient empirically, its theoretical properties have not been clarified yet and no finite sample bound of a convergence rate is known. Another example is Stein points (SP), which minimizes kernelized Stein discrepancy directly. The finite sample bound of SP is $\mathcal{O}(\sqrt{\log{N}/N})$ for $N$ particles, which is computationally inefficient empirically, especially in high-dimensional problems. In this paper, we propose a novel method named \emph{Frank-Wolfe Stein sampling}, which minimizes the maximum mean discrepancy in a greedy way. Our method is computationally efficient empirically and theoretically achieves a faster convergence rate, $\mathcal{O}(e^{-N})$. Numerical experiments show the superiority of our method.