Classification from Triplet Comparison Data
Paper and Code
Aug 05, 2019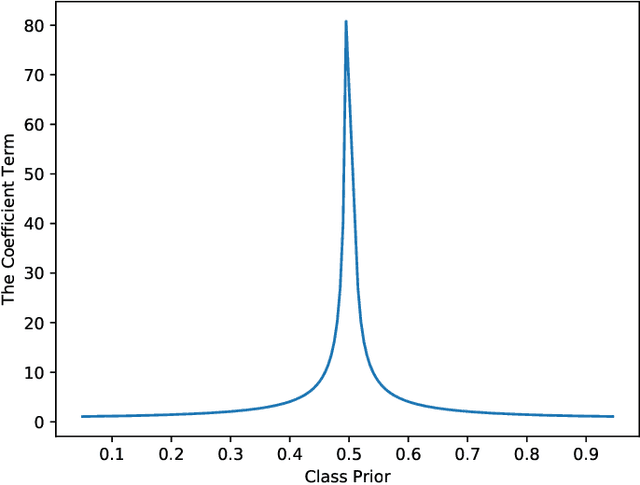
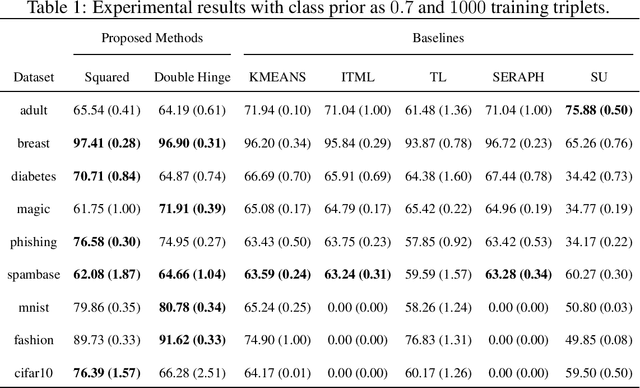
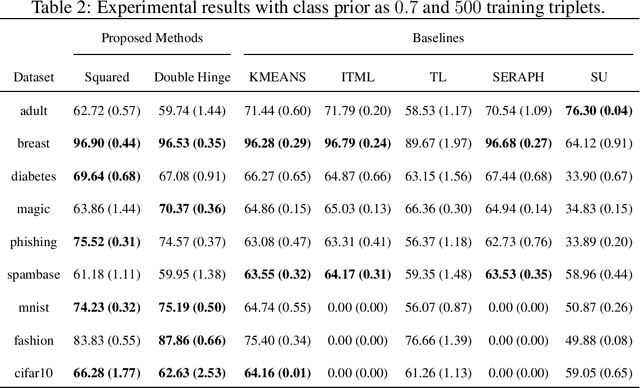
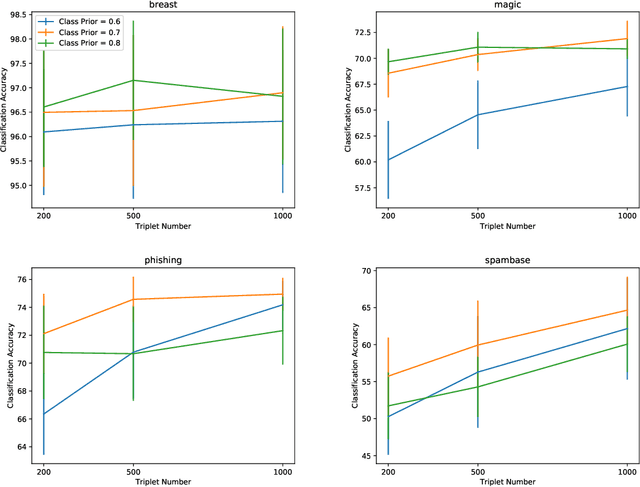
Learning from triplet comparison data has been extensively studied in the context of metric learning, where we want to learn a distance metric between two instances, and ordinal embedding, where we want to learn an embedding in an Euclidean space of the given instances that preserves the comparison order as well as possible. Unlike fully-labeled data, triplet comparison data can be collected in a more accurate and human-friendly way. Although learning from triplet comparison data has been considered in many applications, an important fundamental question of whether we can learn a classifier only from triplet comparison data has remained unanswered. In this paper, we give a positive answer to this important question by proposing an unbiased estimator for the classification risk under the empirical risk minimization framework. Since the proposed method is based on the empirical risk minimization framework, it inherently has the advantage that any surrogate loss function and any model, including neural networks, can be easily applied. Furthermore, we theoretically establish an estimation error bound for the proposed empirical risk minimizer. Finally, we provide experimental results to show that our method empirically works well and outperforms various baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge