A Further Efficient Algorithm with Best-of-Both-Worlds Guarantees for $m$-Set Semi-Bandit Problem

This paper studies the optimality and complexity of Follow-the-Perturbed-Leader (FTPL) policy in $m$-set semi-bandit problems. FTPL has been studied extensively as a promising candidate of an efficient algorithm with favorable regret for adversarial combinatorial semi-bandits. Nevertheless, the optimality of FTPL has still been unknown unlike Follow-the-Regularized-Leader (FTRL) whose optimality has been proved for various tasks of online learning. In this paper, we extend the analysis of FTPL with geometric resampling (GR) to $m$-set semi-bandits, which is a special case of combinatorial semi-bandits, showing that FTPL with Fréchet and Pareto distributions with certain parameters achieves the best possible regret of $O(\sqrt{mdT})$ in adversarial setting. We also show that FTPL with Fréchet and Pareto distributions with a certain parameter achieves a logarithmic regret for stochastic setting, meaning the Best-of-Both-Worlds optimality of FTPL for $m$-set semi-bandit problems. Furthermore, we extend the conditional geometric resampling to $m$-set semi-bandits for efficient loss estimation in FTPL, reducing the computational complexity from $O(d^2)$ of the original geometric resampling to $O(md(\log(d/m)+1))$ without sacrificing the regret performance.

Note on Follow-the-Perturbed-Leader in Combinatorial Semi-Bandit Problems

This paper studies the optimality and complexity of Follow-the-Perturbed-Leader (FTPL) policy in size-invariant combinatorial semi-bandit problems. Recently, Honda et al. (2023) and Lee et al. (2024) showed that FTPL achieves Best-of-Both-Worlds (BOBW) optimality in standard multi-armed bandit problems with Fr\'{e}chet-type distributions. However, the optimality of FTPL in combinatorial semi-bandit problems remains unclear. In this paper, we consider the regret bound of FTPL with geometric resampling (GR) in size-invariant semi-bandit setting, showing that FTPL respectively achieves $O\left(\sqrt{m^2 d^\frac{1}{\alpha}T}+\sqrt{mdT}\right)$ regret with Fr\'{e}chet distributions, and the best possible regret bound of $O\left(\sqrt{mdT}\right)$ with Pareto distributions in adversarial setting. Furthermore, we extend the conditional geometric resampling (CGR) to size-invariant semi-bandit setting, which reduces the computational complexity from $O(d^2)$ of original GR to $O\left(md\left(\log(d/m)+1\right)\right)$ without sacrificing the regret performance of FTPL.

Optimal Regret of Bernoulli Bandits under Global Differential Privacy

As sequential learning algorithms are increasingly applied to real life, ensuring data privacy while maintaining their utilities emerges as a timely question. In this context, regret minimisation in stochastic bandits under $\epsilon$-global Differential Privacy (DP) has been widely studied. Unlike bandits without DP, there is a significant gap between the best-known regret lower and upper bound in this setting, though they "match" in order. Thus, we revisit the regret lower and upper bounds of $\epsilon$-global DP algorithms for Bernoulli bandits and improve both. First, we prove a tighter regret lower bound involving a novel information-theoretic quantity characterising the hardness of $\epsilon$-global DP in stochastic bandits. Our lower bound strictly improves on the existing ones across all $\epsilon$ values. Then, we choose two asymptotically optimal bandit algorithms, i.e. DP-KLUCB and DP-IMED, and propose their DP versions using a unified blueprint, i.e., (a) running in arm-dependent phases, and (b) adding Laplace noise to achieve privacy. For Bernoulli bandits, we analyse the regrets of these algorithms and show that their regrets asymptotically match our lower bound up to a constant arbitrary close to 1. This refutes the conjecture that forgetting past rewards is necessary to design optimal bandit algorithms under global DP. At the core of our algorithms lies a new concentration inequality for sums of Bernoulli variables under Laplace mechanism, which is a new DP version of the Chernoff bound. This result is universally useful as the DP literature commonly treats the concentrations of Laplace noise and random variables separately, while we couple them to yield a tighter bound.

Multi-Player Approaches for Dueling Bandits

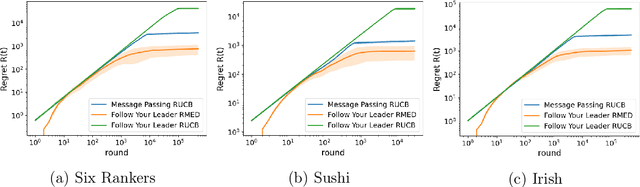
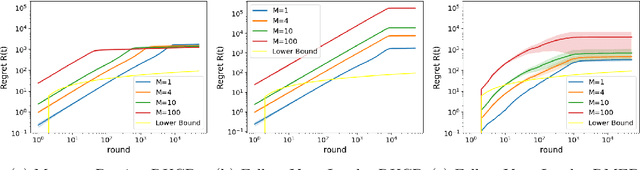
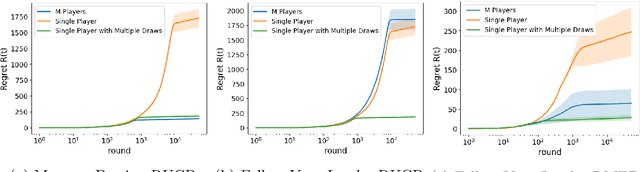
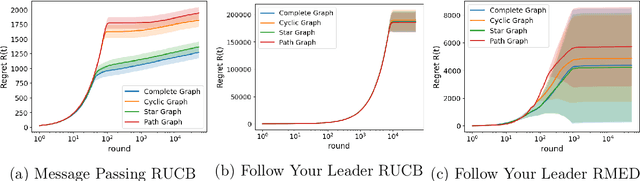
Various approaches have emerged for multi-armed bandits in distributed systems. The multiplayer dueling bandit problem, common in scenarios with only preference-based information like human feedback, introduces challenges related to controlling collaborative exploration of non-informative arm pairs, but has received little attention. To fill this gap, we demonstrate that the direct use of a Follow Your Leader black-box approach matches the lower bound for this setting when utilizing known dueling bandit algorithms as a foundation. Additionally, we analyze a message-passing fully distributed approach with a novel Condorcet-winner recommendation protocol, resulting in expedited exploration in many cases. Our experimental comparisons reveal that our multiplayer algorithms surpass single-player benchmark algorithms, underscoring their efficacy in addressing the nuanced challenges of the multiplayer dueling bandit setting.

Learning with Posterior Sampling for Revenue Management under Time-varying Demand

This paper discusses the revenue management (RM) problem to maximize revenue by pricing items or services. One challenge in this problem is that the demand distribution is unknown and varies over time in real applications such as airline and retail industries. In particular, the time-varying demand has not been well studied under scenarios of unknown demand due to the difficulty of jointly managing the remaining inventory and estimating the demand. To tackle this challenge, we first introduce an episodic generalization of the RM problem motivated by typical application scenarios. We then propose a computationally efficient algorithm based on posterior sampling, which effectively optimizes prices by solving linear programming. We derive a Bayesian regret upper bound of this algorithm for general models where demand parameters can be correlated between time periods, while also deriving a regret lower bound for generic algorithms. Our empirical study shows that the proposed algorithm performs better than other benchmark algorithms and comparably to the optimal policy in hindsight. We also propose a heuristic modification of the proposed algorithm, which further efficiently learns the pricing policy in the experiments.

Adaptive Learning Rate for Follow-the-Regularized-Leader: Competitive Analysis and Best-of-Both-Worlds

Follow-The-Regularized-Leader (FTRL) is known as an effective and versatile approach in online learning, where appropriate choice of the learning rate is crucial for smaller regret. To this end, we formulate the problem of adjusting FTRL's learning rate as a sequential decision-making problem and introduce the framework of competitive analysis. We establish a lower bound for the competitive ratio and propose update rules for learning rate that achieves an upper bound within a constant factor of this lower bound. Specifically, we illustrate that the optimal competitive ratio is characterized by the (approximate) monotonicity of components of the penalty term, showing that a constant competitive ratio is achievable if the components of the penalty term form a monotonically non-increasing sequence, and derive a tight competitive ratio when penalty terms are $\xi$-approximately monotone non-increasing. Our proposed update rule, referred to as \textit{stability-penalty matching}, also facilitates constructing the Best-Of-Both-Worlds (BOBW) algorithms for stochastic and adversarial environments. In these environments our result contributes to achieve tighter regret bound and broaden the applicability of algorithms for various settings such as multi-armed bandits, graph bandits, linear bandits, and contextual bandits.

Follow-the-Perturbed-Leader with Fréchet-type Tail Distributions: Optimality in Adversarial Bandits and Best-of-Both-Worlds

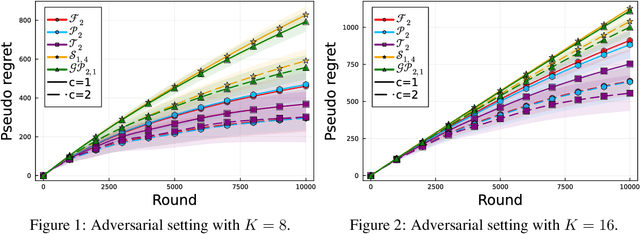
This paper studies the optimality of the Follow-the-Perturbed-Leader (FTPL) policy in both adversarial and stochastic $K$-armed bandits. Despite the widespread use of the Follow-the-Regularized-Leader (FTRL) framework with various choices of regularization, the FTPL framework, which relies on random perturbations, has not received much attention, despite its inherent simplicity. In adversarial bandits, there has been conjecture that FTPL could potentially achieve $\mathcal{O}(\sqrt{KT})$ regrets if perturbations follow a distribution with a Fr\'{e}chet-type tail. Recent work by Honda et al. (2023) showed that FTPL with Fr\'{e}chet distribution with shape $\alpha=2$ indeed attains this bound and, notably logarithmic regret in stochastic bandits, meaning the Best-of-Both-Worlds (BOBW) capability of FTPL. However, this result only partly resolves the above conjecture because their analysis heavily relies on the specific form of the Fr\'{e}chet distribution with this shape. In this paper, we establish a sufficient condition for perturbations to achieve $\mathcal{O}(\sqrt{KT})$ regrets in the adversarial setting, which covers, e.g., Fr\'{e}chet, Pareto, and Student-$t$ distributions. We also demonstrate the BOBW achievability of FTPL with certain Fr\'{e}chet-type tail distributions. Our results contribute not only to resolving existing conjectures through the lens of extreme value theory but also potentially offer insights into the effect of the regularization functions in FTRL through the mapping from FTPL to FTRL.

Exploration by Optimization with Hybrid Regularizers: Logarithmic Regret with Adversarial Robustness in Partial Monitoring

Partial monitoring is a generic framework of online decision-making problems with limited observations. To make decisions from such limited observations, it is necessary to find an appropriate distribution for exploration. Recently, a powerful approach for this purpose, exploration by optimization (ExO), was proposed, which achieves the optimal bounds in adversarial environments with follow-the-regularized-leader for a wide range of online decision-making problems. However, a naive application of ExO in stochastic environments significantly degrades regret bounds. To resolve this problem in locally observable games, we first establish a novel framework and analysis for ExO with a hybrid regularizer. This development allows us to significantly improve the existing regret bounds of best-of-both-worlds (BOBW) algorithms, which achieves nearly optimal bounds both in stochastic and adversarial environments. In particular, we derive a stochastic regret bound of $O(\sum_{a \neq a^*} k^2 m^2 \log T / \Delta_a)$, where $k$, $m$, and $T$ are the numbers of actions, observations and rounds, $a^*$ is an optimal action, and $\Delta_a$ is the suboptimality gap for action $a$. This bound is roughly $\Theta(k^2 \log T)$ times smaller than existing BOBW bounds. In addition, for globally observable games, we provide a new BOBW algorithm with the first $O(\log T)$ stochastic bound.

Thompson Exploration with Best Challenger Rule in Best Arm Identification

This paper studies the fixed-confidence best arm identification (BAI) problem in the bandit framework in the canonical single-parameter exponential models. For this problem, many policies have been proposed, but most of them require solving an optimization problem at every round and/or are forced to explore an arm at least a certain number of times except those restricted to the Gaussian model. To address these limitations, we propose a novel policy that combines Thompson sampling with a computationally efficient approach known as the best challenger rule. While Thompson sampling was originally considered for maximizing the cumulative reward, we demonstrate that it can be used to naturally explore arms in BAI without forcing it. We show that our policy is asymptotically optimal for any two-armed bandit problems and achieves near optimality for general $K$-armed bandit problems for $K\geq 3$. Nevertheless, in numerical experiments, our policy shows competitive performance compared to asymptotically optimal policies in terms of sample complexity while requiring less computation cost. In addition, we highlight the advantages of our policy by comparing it to the concept of $\beta$-optimality, a relaxed notion of asymptotic optimality commonly considered in the analysis of a class of policies including the proposed one.

Stability-penalty-adaptive Follow-the-regularized-leader: Sparsity, Game-dependency, and Best-of-both-worlds

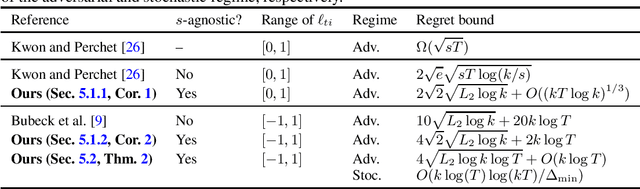
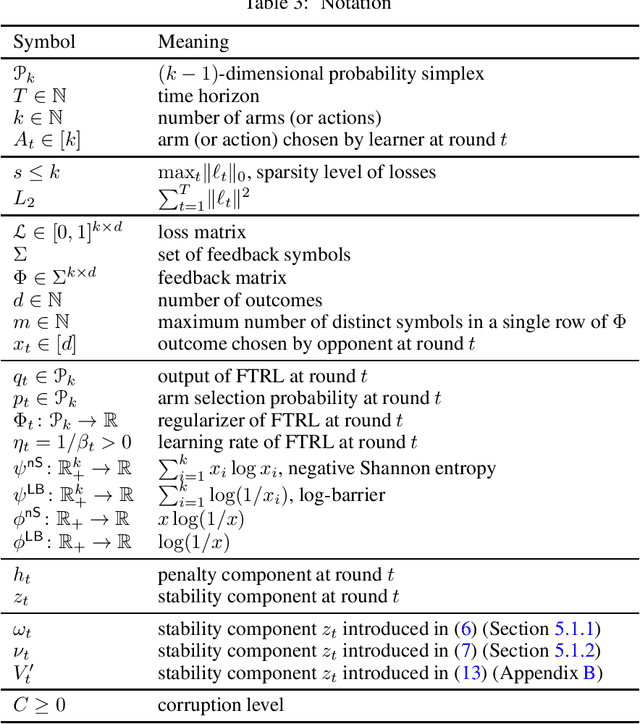
Adaptivity to the difficulties of a problem is a key property in sequential decision-making problems to broaden the applicability of algorithms. Follow-the-Regularized-Leader (FTRL) has recently emerged as one of the most promising approaches for obtaining various types of adaptivity in bandit problems. Aiming to further generalize this adaptivity, we develop a generic adaptive learning rate, called Stability-Penalty-Adaptive (SPA) learning rate for FTRL. This learning rate yields a regret bound jointly depending on stability and penalty of the algorithm, into which the regret of FTRL is typically decomposed. With this result, we establish several algorithms with three types of adaptivity: sparsity, game-dependency, and Best-of-Both-Worlds (BOBW). Sparsity frequently appears in real-world problems. However, existing sparse multi-armed bandit algorithms with $k$-arms assume that the sparsity level $s \leq k$ is known in advance, which is often not the case in real-world scenarios. To address this problem, with the help of the new learning rate framework, we establish $s$-agnostic algorithms with regret bounds of $\tilde{O}(\sqrt{sT})$ in the adversarial regime for $T$ rounds, which matches the existing lower bound up to a logarithmic factor. Meanwhile, BOBW algorithms aim to achieve a near-optimal regret in both the stochastic and adversarial regimes. Leveraging the new adaptive learning rate framework and a novel analysis to bound the variation in FTRL output in response to changes in a regularizer, we establish the first BOBW algorithm with a sparsity-dependent bound. Additionally, we explore partial monitoring and demonstrate that the proposed learning rate framework allows us to achieve a game-dependent bound and the BOBW simultaneously.