Follow-the-Perturbed-Leader with Fréchet-type Tail Distributions: Optimality in Adversarial Bandits and Best-of-Both-Worlds
Paper and Code
Mar 08, 2024
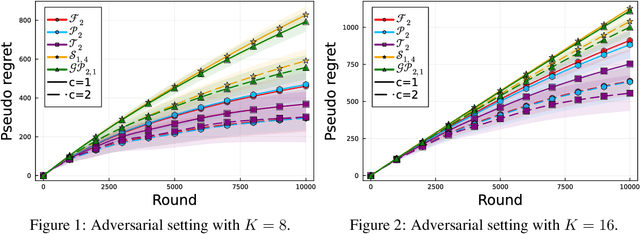

This paper studies the optimality of the Follow-the-Perturbed-Leader (FTPL) policy in both adversarial and stochastic $K$-armed bandits. Despite the widespread use of the Follow-the-Regularized-Leader (FTRL) framework with various choices of regularization, the FTPL framework, which relies on random perturbations, has not received much attention, despite its inherent simplicity. In adversarial bandits, there has been conjecture that FTPL could potentially achieve $\mathcal{O}(\sqrt{KT})$ regrets if perturbations follow a distribution with a Fr\'{e}chet-type tail. Recent work by Honda et al. (2023) showed that FTPL with Fr\'{e}chet distribution with shape $\alpha=2$ indeed attains this bound and, notably logarithmic regret in stochastic bandits, meaning the Best-of-Both-Worlds (BOBW) capability of FTPL. However, this result only partly resolves the above conjecture because their analysis heavily relies on the specific form of the Fr\'{e}chet distribution with this shape. In this paper, we establish a sufficient condition for perturbations to achieve $\mathcal{O}(\sqrt{KT})$ regrets in the adversarial setting, which covers, e.g., Fr\'{e}chet, Pareto, and Student-$t$ distributions. We also demonstrate the BOBW achievability of FTPL with certain Fr\'{e}chet-type tail distributions. Our results contribute not only to resolving existing conjectures through the lens of extreme value theory but also potentially offer insights into the effect of the regularization functions in FTRL through the mapping from FTPL to FTRL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge