EUGens: Efficient, Unified, and General Dense Layers

Efficient neural networks are essential for scaling machine learning models to real-time applications and resource-constrained environments. Fully-connected feedforward layers (FFLs) introduce computation and parameter count bottlenecks within neural network architectures. To address this challenge, in this work, we propose a new class of dense layers that generalize standard fully-connected feedforward layers, \textbf{E}fficient, \textbf{U}nified and \textbf{Gen}eral dense layers (EUGens). EUGens leverage random features to approximate standard FFLs and go beyond them by incorporating a direct dependence on the input norms in their computations. The proposed layers unify existing efficient FFL extensions and improve efficiency by reducing inference complexity from quadratic to linear time. They also lead to \textbf{the first} unbiased algorithms approximating FFLs with arbitrary polynomial activation functions. Furthermore, EuGens reduce the parameter count and computational overhead while preserving the expressive power and adaptability of FFLs. We also present a layer-wise knowledge transfer technique that bypasses backpropagation, enabling efficient adaptation of EUGens to pre-trained models. Empirically, we observe that integrating EUGens into Transformers and MLPs yields substantial improvements in inference speed (up to \textbf{27}\%) and memory efficiency (up to \textbf{30}\%) across a range of tasks, including image classification, language model pre-training, and 3D scene reconstruction. Overall, our results highlight the potential of EUGens for the scalable deployment of large-scale neural networks in real-world scenarios.

Convergence of Muon with Newton-Schulz

We analyze Muon as originally proposed and used in practice -- using the momentum orthogonalization with a few Newton-Schulz steps. The prior theoretical results replace this key step in Muon with an exact SVD-based polar factor. We prove that Muon with Newton-Schulz converges to a stationary point at the same rate as the SVD-polar idealization, up to a constant factor for a given number $q$ of Newton-Schulz steps. We further analyze this constant factor and prove that it converges to 1 doubly exponentially in $q$ and improves with the degree of the polynomial used in Newton-Schulz for approximating the orthogonalization direction. We also prove that Muon removes the typical square-root-of-rank loss compared to its vector-based counterpart, SGD with momentum. Our results explain why Muon with a few low-degree Newton-Schulz steps matches exact-polar (SVD) behavior at a much faster wall-clock time and explain how much momentum matrix orthogonalization via Newton-Schulz benefits over the vector-based optimizer. Overall, our theory justifies the practical Newton-Schulz design of Muon, narrowing its practice-theory gap.

Tractable Multinomial Logit Contextual Bandits with Non-Linear Utilities

We study the multinomial logit (MNL) contextual bandit problem for sequential assortment selection. Although most existing research assumes utility functions to be linear in item features, this linearity assumption restricts the modeling of intricate interactions between items and user preferences. A recent work (Zhang & Luo, 2024) has investigated general utility function classes, yet its method faces fundamental trade-offs between computational tractability and statistical efficiency. To address this limitation, we propose a computationally efficient algorithm for MNL contextual bandits leveraging the upper confidence bound principle, specifically designed for non-linear parametric utility functions, including those modeled by neural networks. Under a realizability assumption and a mild geometric condition on the utility function class, our algorithm achieves a regret bound of $\tilde{O}(\sqrt{T})$, where $T$ denotes the total number of rounds. Our result establishes that sharp $\tilde{O}(\sqrt{T})$-regret is attainable even with neural network-based utilities, without relying on strong assumptions such as neural tangent kernel approximations. To the best of our knowledge, our proposed method is the first computationally tractable algorithm for MNL contextual bandits with non-linear utilities that provably attains $\tilde{O}(\sqrt{T})$ regret. Comprehensive numerical experiments validate the effectiveness of our approach, showing robust performance not only in realizable settings but also in scenarios with model misspecification.

Infrequent Exploration in Linear Bandits

We study the problem of infrequent exploration in linear bandits, addressing a significant yet overlooked gap between fully adaptive exploratory methods (e.g., UCB and Thompson Sampling), which explore potentially at every time step, and purely greedy approaches, which require stringent diversity assumptions to succeed. Continuous exploration can be impractical or unethical in safety-critical or costly domains, while purely greedy strategies typically fail without adequate contextual diversity. To bridge these extremes, we introduce a simple and practical framework, INFEX, explicitly designed for infrequent exploration. INFEX executes a base exploratory policy according to a given schedule while predominantly choosing greedy actions in between. Despite its simplicity, our theoretical analysis demonstrates that INFEX achieves instance-dependent regret matching standard provably efficient algorithms, provided the exploration frequency exceeds a logarithmic threshold. Additionally, INFEX is a general, modular framework that allows seamless integration of any fully adaptive exploration method, enabling wide applicability and ease of adoption. By restricting intensive exploratory computations to infrequent intervals, our approach can also enhance computational efficiency. Empirical evaluations confirm our theoretical findings, showing state-of-the-art regret performance and runtime improvements over existing methods.

Batched Stochastic Matching Bandits

In this study, we introduce a novel bandit framework for stochastic matching based on the Multi-nomial Logit (MNL) choice model. In our setting, $N$ agents on one side are assigned to $K$ arms on the other side, where each arm stochastically selects an agent from its assigned pool according to an unknown preference and yields a corresponding reward. The objective is to minimize regret by maximizing the cumulative revenue from successful matches across all agents. This task requires solving a combinatorial optimization problem based on estimated preferences, which is NP-hard and leads a naive approach to incur a computational cost of $O(K^N)$ per round. To address this challenge, we propose batched algorithms that limit the frequency of matching updates, thereby reducing the amortized computational cost (i.e., the average cost per round) to $O(1)$ while still achieving a regret bound of $\tilde{O}(\sqrt{T})$.

AI Should Sense Better, Not Just Scale Bigger: Adaptive Sensing as a Paradigm Shift

Current AI advances largely rely on scaling neural models and expanding training datasets to achieve generalization and robustness. Despite notable successes, this paradigm incurs significant environmental, economic, and ethical costs, limiting sustainability and equitable access. Inspired by biological sensory systems, where adaptation occurs dynamically at the input (e.g., adjusting pupil size, refocusing vision)--we advocate for adaptive sensing as a necessary and foundational shift. Adaptive sensing proactively modulates sensor parameters (e.g., exposure, sensitivity, multimodal configurations) at the input level, significantly mitigating covariate shifts and improving efficiency. Empirical evidence from recent studies demonstrates that adaptive sensing enables small models (e.g., EfficientNet-B0) to surpass substantially larger models (e.g., OpenCLIP-H) trained with significantly more data and compute. We (i) outline a roadmap for broadly integrating adaptive sensing into real-world applications spanning humanoid, healthcare, autonomous systems, agriculture, and environmental monitoring, (ii) critically assess technical and ethical integration challenges, and (iii) propose targeted research directions, such as standardized benchmarks, real-time adaptive algorithms, multimodal integration, and privacy-preserving methods. Collectively, these efforts aim to transition the AI community toward sustainable, robust, and equitable artificial intelligence systems.

Experimental Design for Semiparametric Bandits

We study finite-armed semiparametric bandits, where each arm's reward combines a linear component with an unknown, potentially adversarial shift. This model strictly generalizes classical linear bandits and reflects complexities common in practice. We propose the first experimental-design approach that simultaneously offers a sharp regret bound, a PAC bound, and a best-arm identification guarantee. Our method attains the minimax regret $\tilde{O}(\sqrt{dT})$, matching the known lower bound for finite-armed linear bandits, and further achieves logarithmic regret under a positive suboptimality gap condition. These guarantees follow from our refined non-asymptotic analysis of orthogonalized regression that attains the optimal $\sqrt{d}$ rate, paving the way for robust and efficient learning across a broad class of semiparametric bandit problems.

Dynamic Assortment Selection and Pricing with Censored Preference Feedback

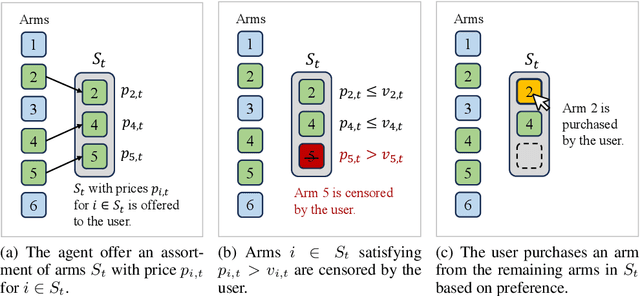
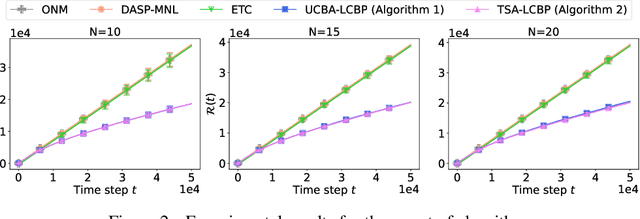
In this study, we investigate the problem of dynamic multi-product selection and pricing by introducing a novel framework based on a \textit{censored multinomial logit} (C-MNL) choice model. In this model, sellers present a set of products with prices, and buyers filter out products priced above their valuation, purchasing at most one product from the remaining options based on their preferences. The goal is to maximize seller revenue by dynamically adjusting product offerings and prices, while learning both product valuations and buyer preferences through purchase feedback. To achieve this, we propose a Lower Confidence Bound (LCB) pricing strategy. By combining this pricing strategy with either an Upper Confidence Bound (UCB) or Thompson Sampling (TS) product selection approach, our algorithms achieve regret bounds of $\tilde{O}(d^{\frac{3}{2}}\sqrt{T/\kappa})$ and $\tilde{O}(d^{2}\sqrt{T/\kappa})$, respectively. Finally, we validate the performance of our methods through simulations, demonstrating their effectiveness.

Adversarial Policy Optimization for Offline Preference-based Reinforcement Learning

In this paper, we study offline preference-based reinforcement learning (PbRL), where learning is based on pre-collected preference feedback over pairs of trajectories. While offline PbRL has demonstrated remarkable empirical success, existing theoretical approaches face challenges in ensuring conservatism under uncertainty, requiring computationally intractable confidence set constructions. We address this limitation by proposing Adversarial Preference-based Policy Optimization (APPO), a computationally efficient algorithm for offline PbRL that guarantees sample complexity bounds without relying on explicit confidence sets. By framing PbRL as a two-player game between a policy and a model, our approach enforces conservatism in a tractable manner. Using standard assumptions on function approximation and bounded trajectory concentrability, we derive a sample complexity bound. To our knowledge, APPO is the first offline PbRL algorithm to offer both statistical efficiency and practical applicability. Experimental results on continuous control tasks demonstrate that APPO effectively learns from complex datasets, showing comparable performance with existing state-of-the-art methods.

Linear Bandits with Partially Observable Features

We introduce a novel linear bandit problem with partially observable features, resulting in partial reward information and spurious estimates. Without proper address for latent part, regret possibly grows linearly in decision horizon $T$, as their influence on rewards are unknown. To tackle this, we propose a novel analysis to handle the latent features and an algorithm that achieves sublinear regret. The core of our algorithm involves (i) augmenting basis vectors orthogonal to the observed feature space, and (ii) introducing an efficient doubly robust estimator. Our approach achieves a regret bound of $\tilde{O}(\sqrt{(d + d_h)T})$, where $d$ is the dimension of observed features, and $d_h$ is the unknown dimension of the subspace of the unobserved features. Notably, our algorithm requires no prior knowledge of the unobserved feature space, which may expand as more features become hidden. Numerical experiments confirm that our algorithm outperforms both non-contextual multi-armed bandits and linear bandit algorithms depending solely on observed features.