Pursuing Overall Welfare in Federated Learning through Sequential Decision Making

In traditional federated learning, a single global model cannot perform equally well for all clients. Therefore, the need to achieve the client-level fairness in federated system has been emphasized, which can be realized by modifying the static aggregation scheme for updating the global model to an adaptive one, in response to the local signals of the participating clients. Our work reveals that existing fairness-aware aggregation strategies can be unified into an online convex optimization framework, in other words, a central server's sequential decision making process. To enhance the decision making capability, we propose simple and intuitive improvements for suboptimal designs within existing methods, presenting AAggFF. Considering practical requirements, we further subdivide our method tailored for the cross-device and the cross-silo settings, respectively. Theoretical analyses guarantee sublinear regret upper bounds for both settings: $\mathcal{O}(\sqrt{T \log{K}})$ for the cross-device setting, and $\mathcal{O}(K \log{T})$ for the cross-silo setting, with $K$ clients and $T$ federation rounds. Extensive experiments demonstrate that the federated system equipped with AAggFF achieves better degree of client-level fairness than existing methods in both practical settings. Code is available at https://github.com/vaseline555/AAggFF

Bandit-supported care planning for older people with complex health and care needs

Long-term care service for old people is in great demand in most of the aging societies. The number of nursing homes residents is increasing while the number of care providers is limited. Due to the care worker shortage, care to vulnerable older residents cannot be fully tailored to the unique needs and preference of each individual. This may bring negative impacts on health outcomes and quality of life among institutionalized older people. To improve care quality through personalized care planning and delivery with limited care workforce, we propose a new care planning model assisted by artificial intelligence. We apply bandit algorithms which optimize the clinical decision for care planning by adapting to the sequential feedback from the past decisions. We evaluate the proposed model on empirical data acquired from the Systems for Person-centered Elder Care (SPEC) study, a ICT-enhanced care management program.

GBOSE: Generalized Bandit Orthogonalized Semiparametric Estimation

In sequential decision-making scenarios i.e., mobile health recommendation systems revenue management contextual multi-armed bandit algorithms have garnered attention for their performance. But most of the existing algorithms are built on the assumption of a strictly parametric reward model mostly linear in nature. In this work we propose a new algorithm with a semi-parametric reward model with state-of-the-art complexity of upper bound on regret amongst existing semi-parametric algorithms. Our work expands the scope of another representative algorithm of state-of-the-art complexity with a similar reward model by proposing an algorithm built upon the same action filtering procedures but provides explicit action selection distribution for scenarios involving more than two arms at a particular time step while requiring fewer computations. We derive the said complexity of the upper bound on regret and present simulation results that affirm our methods superiority out of all prevalent semi-parametric bandit algorithms for cases involving over two arms.

Robust Tests in Online Decision-Making

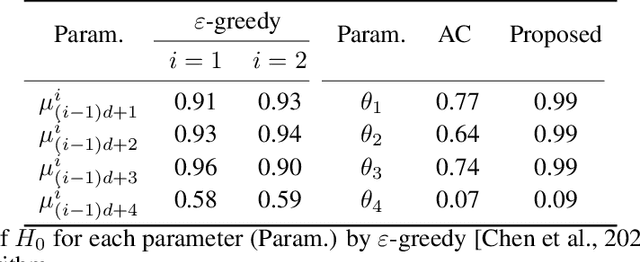
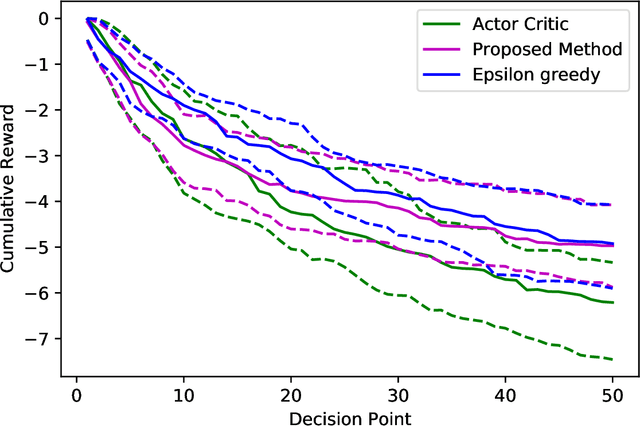
Bandit algorithms are widely used in sequential decision problems to maximize the cumulative reward. One potential application is mobile health, where the goal is to promote the user's health through personalized interventions based on user specific information acquired through wearable devices. Important considerations include the type of, and frequency with which data is collected (e.g. GPS, or continuous monitoring), as such factors can severely impact app performance and users' adherence. In order to balance the need to collect data that is useful with the constraint of impacting app performance, one needs to be able to assess the usefulness of variables. Bandit feedback data are sequentially correlated, so traditional testing procedures developed for independent data cannot apply. Recently, a statistical testing procedure was developed for the actor-critic bandit algorithm. An actor-critic algorithm maintains two separate models, one for the actor, the action selection policy, and the other for the critic, the reward model. The performance of the algorithm as well as the validity of the test are guaranteed only when the critic model is correctly specified. However, misspecification is frequent in practice due to incorrect functional form or missing covariates. In this work, we propose a modified actor-critic algorithm which is robust to critic misspecification and derive a novel testing procedure for the actor parameters in this case.

Semi-Parametric Contextual Bandits with Graph-Laplacian Regularization

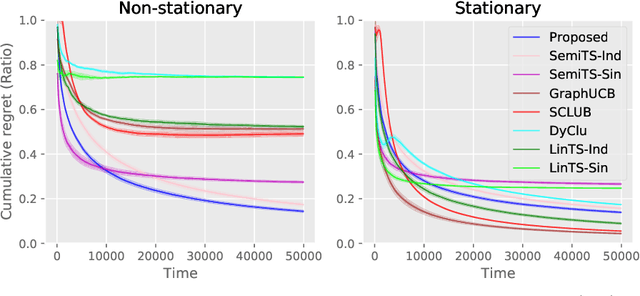
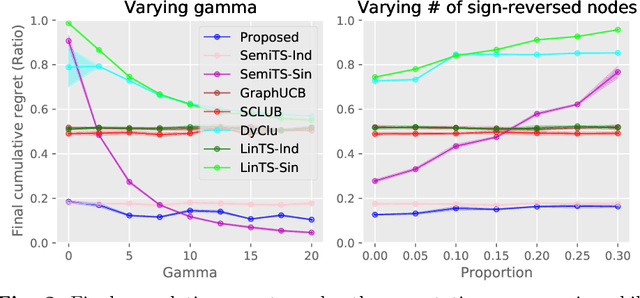
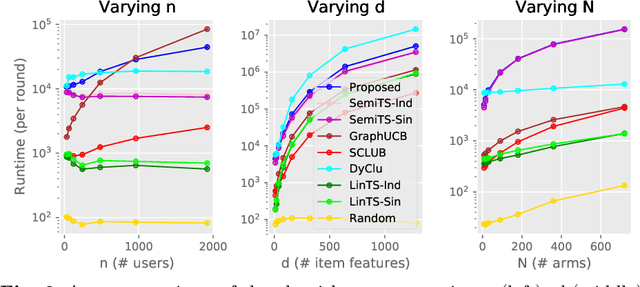
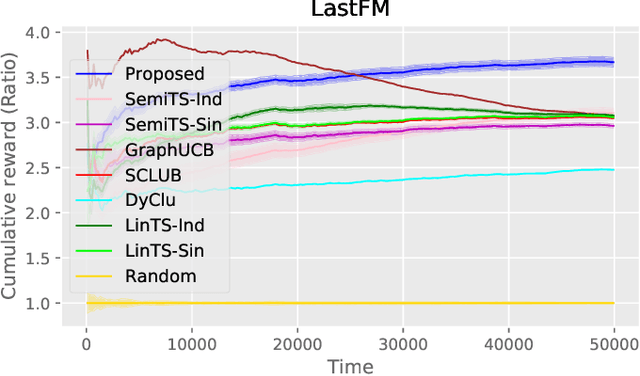
Non-stationarity is ubiquitous in human behavior and addressing it in the contextual bandits is challenging. Several works have addressed the problem by investigating semi-parametric contextual bandits and warned that ignoring non-stationarity could harm performances. Another prevalent human behavior is social interaction which has become available in a form of a social network or graph structure. As a result, graph-based contextual bandits have received much attention. In this paper, we propose "SemiGraphTS," a novel contextual Thompson-sampling algorithm for a graph-based semi-parametric reward model. Our algorithm is the first to be proposed in this setting. We derive an upper bound of the cumulative regret that can be expressed as a multiple of a factor depending on the graph structure and the order for the semi-parametric model without a graph. We evaluate the proposed and existing algorithms via simulation and real data example.

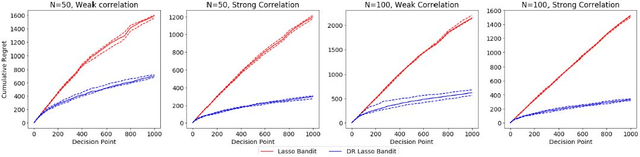
Doubly-Robust Lasso Bandit

Contextual multi-armed bandit algorithms are widely used in sequential decision tasks such as news article recommendation systems, web page ad placement algorithms, and mobile health. Most of the existing algorithms have regret proportional to a polynomial function of the context dimension, $d$. In many applications however, it is often the case that contexts are high-dimensional with only a sparse subset of size $s_0 (\ll d)$ being correlated with the reward. We propose a novel algorithm, namely the Doubly-Robust Lasso Bandit algorithm, which exploits the sparse structure as in Lasso, while blending the doubly-robust technique used in missing data literature. The high-probability upper bound of the regret incurred by the proposed algorithm does not depend on the number of arms, has better dependency on $s_0$ than previous works, and scales with $\mathrm{log}(d)$ instead of a polynomial function of $d$. The proposed algorithm shows good performance when contexts of different arms are correlated and requires less tuning parameters than existing methods.

Contextual Multi-armed Bandit Algorithm for Semiparametric Reward Model

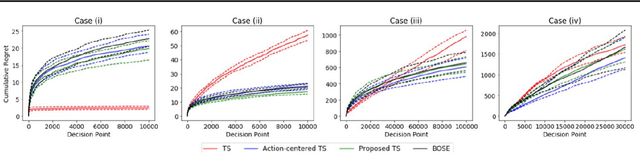
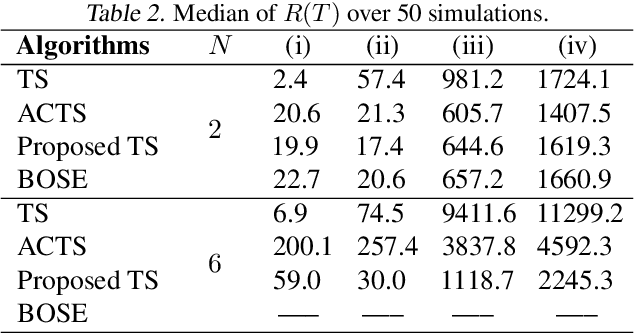
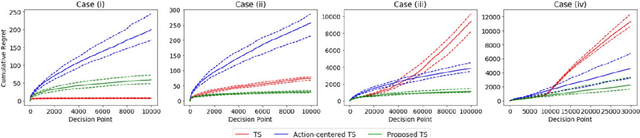
Contextual multi-armed bandit (MAB) algorithms have been shown promising for maximizing cumulative rewards in sequential decision tasks such as news article recommendation systems, web page ad placement algorithms, and mobile health. However, most of the proposed contextual MAB algorithms assume linear relationships between the reward and the context of the action. This paper proposes a new contextual MAB algorithm for a relaxed, semiparametric reward model that supports nonstationarity. The proposed method is less restrictive, easier to implement and faster than two alternative algorithms that consider the same model, while achieving a tight regret upper bound. We prove that the high-probability upper bound of the regret incurred by the proposed algorithm has the same order as the Thompson sampling algorithm for linear reward models. The proposed and existing algorithms are evaluated via simulation and also applied to Yahoo! news article recommendation log data.