Basic Inequalities for First-Order Optimization with Applications to Statistical Risk Analysis

We introduce \textit{basic inequalities} for first-order iterative optimization algorithms, forming a simple and versatile framework that connects implicit and explicit regularization. While related inequalities appear in the literature, we isolate and highlight a specific form and develop it as a well-rounded tool for statistical analysis. Let $f$ denote the objective function to be optimized. Given a first-order iterative algorithm initialized at $θ_0$ with current iterate $θ_T$, the basic inequality upper bounds $f(θ_T)-f(z)$ for any reference point $z$ in terms of the accumulated step sizes and the distances between $θ_0$, $θ_T$, and $z$. The bound translates the number of iterations into an effective regularization coefficient in the loss function. We demonstrate this framework through analyses of training dynamics and prediction risk bounds. In addition to revisiting and refining known results on gradient descent, we provide new results for mirror descent with Bregman divergence projection, for generalized linear models trained by gradient descent and exponentiated gradient descent, and for randomized predictors. We illustrate and supplement these theoretical findings with experiments on generalized linear models.

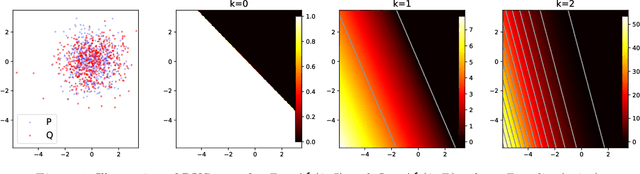
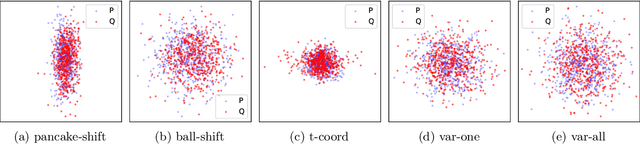
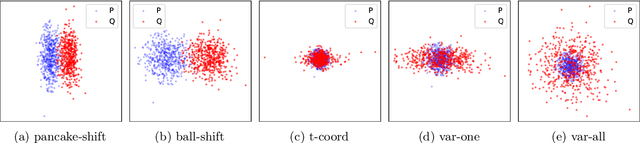
Maximum Mean Discrepancy Meets Neural Networks: The Radon-Kolmogorov-Smirnov Test

Maximum mean discrepancy (MMD) refers to a general class of nonparametric two-sample tests that are based on maximizing the mean difference over samples from one distribution $P$ versus another $Q$, over all choices of data transformations $f$ living in some function space $\mathcal{F}$. Inspired by recent work that connects what are known as functions of $\textit{Radon bounded variation}$ (RBV) and neural networks (Parhi and Nowak, 2021, 2023), we study the MMD defined by taking $\mathcal{F}$ to be the unit ball in the RBV space of a given smoothness order $k \geq 0$. This test, which we refer to as the $\textit{Radon-Kolmogorov-Smirnov}$ (RKS) test, can be viewed as a generalization of the well-known and classical Kolmogorov-Smirnov (KS) test to multiple dimensions and higher orders of smoothness. It is also intimately connected to neural networks: we prove that the witness in the RKS test -- the function $f$ achieving the maximum mean difference -- is always a ridge spline of degree $k$, i.e., a single neuron in a neural network. This allows us to leverage the power of modern deep learning toolkits to (approximately) optimize the criterion that underlies the RKS test. We prove that the RKS test has asymptotically full power at distinguishing any distinct pair $P \not= Q$ of distributions, derive its asymptotic null distribution, and carry out extensive experiments to elucidate the strengths and weakenesses of the RKS test versus the more traditional kernel MMD test.

Semi-Parametric Contextual Bandits with Graph-Laplacian Regularization

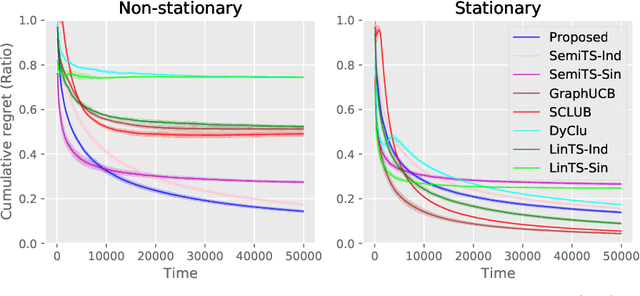
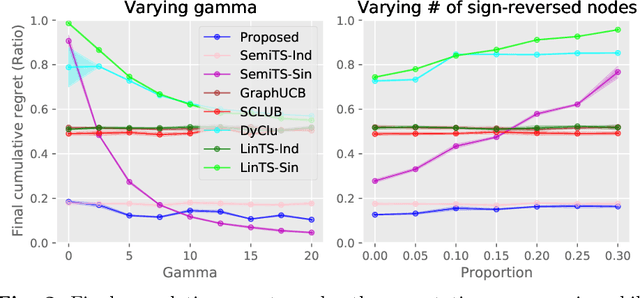
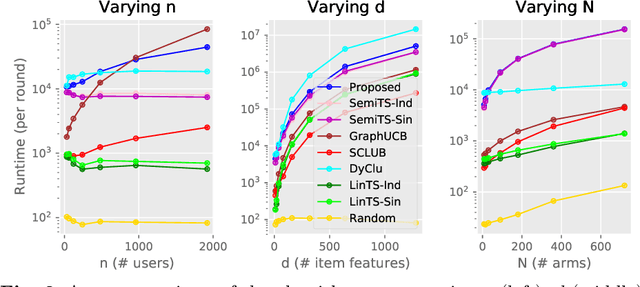
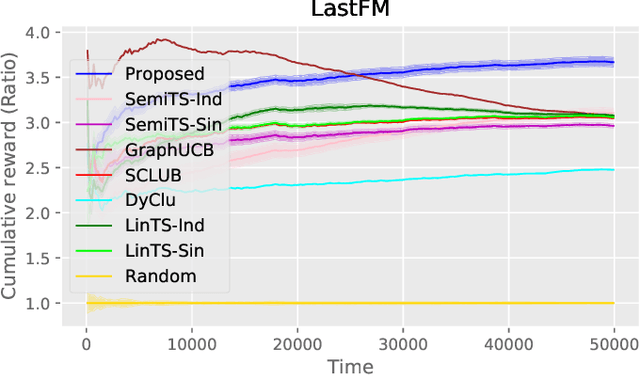
Non-stationarity is ubiquitous in human behavior and addressing it in the contextual bandits is challenging. Several works have addressed the problem by investigating semi-parametric contextual bandits and warned that ignoring non-stationarity could harm performances. Another prevalent human behavior is social interaction which has become available in a form of a social network or graph structure. As a result, graph-based contextual bandits have received much attention. In this paper, we propose "SemiGraphTS," a novel contextual Thompson-sampling algorithm for a graph-based semi-parametric reward model. Our algorithm is the first to be proposed in this setting. We derive an upper bound of the cumulative regret that can be expressed as a multiple of a factor depending on the graph structure and the order for the semi-parametric model without a graph. We evaluate the proposed and existing algorithms via simulation and real data example.