Mean-field variational inference with the TAP free energy: Geometric and statistical properties in linear models

We study mean-field variational inference in a Bayesian linear model when the sample size n is comparable to the dimension p. In high dimensions, the common approach of minimizing a Kullback-Leibler divergence from the posterior distribution, or maximizing an evidence lower bound, may deviate from the true posterior mean and underestimate posterior uncertainty. We study instead minimization of the TAP free energy, showing in a high-dimensional asymptotic framework that it has a local minimizer which provides a consistent estimate of the posterior marginals and may be used for correctly calibrated posterior inference. Geometrically, we show that the landscape of the TAP free energy is strongly convex in an extensive neighborhood of this local minimizer, which under certain general conditions can be found by an Approximate Message Passing (AMP) algorithm. We then exhibit an efficient algorithm that linearly converges to the minimizer within this local neighborhood. In settings where it is conjectured that no efficient algorithm can find this local neighborhood, we prove analogous geometric properties for a local minimizer of the TAP free energy reachable by AMP, and show that posterior inference based on this minimizer remains correctly calibrated.

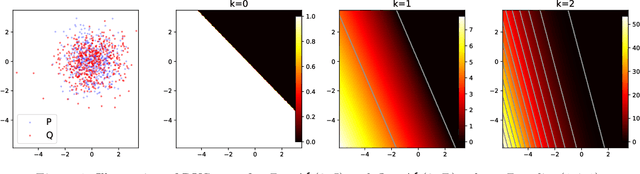
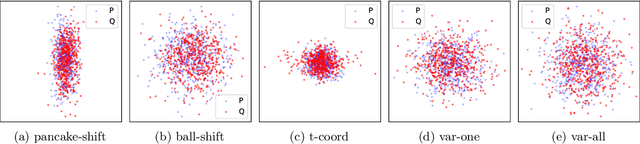
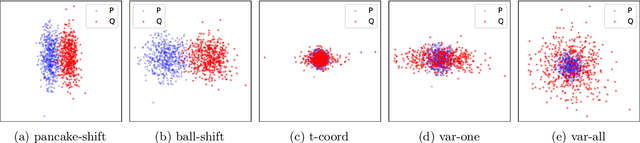
Maximum Mean Discrepancy Meets Neural Networks: The Radon-Kolmogorov-Smirnov Test

Maximum mean discrepancy (MMD) refers to a general class of nonparametric two-sample tests that are based on maximizing the mean difference over samples from one distribution $P$ versus another $Q$, over all choices of data transformations $f$ living in some function space $\mathcal{F}$. Inspired by recent work that connects what are known as functions of $\textit{Radon bounded variation}$ (RBV) and neural networks (Parhi and Nowak, 2021, 2023), we study the MMD defined by taking $\mathcal{F}$ to be the unit ball in the RBV space of a given smoothness order $k \geq 0$. This test, which we refer to as the $\textit{Radon-Kolmogorov-Smirnov}$ (RKS) test, can be viewed as a generalization of the well-known and classical Kolmogorov-Smirnov (KS) test to multiple dimensions and higher orders of smoothness. It is also intimately connected to neural networks: we prove that the witness in the RKS test -- the function $f$ achieving the maximum mean difference -- is always a ridge spline of degree $k$, i.e., a single neuron in a neural network. This allows us to leverage the power of modern deep learning toolkits to (approximately) optimize the criterion that underlies the RKS test. We prove that the RKS test has asymptotically full power at distinguishing any distinct pair $P \not= Q$ of distributions, derive its asymptotic null distribution, and carry out extensive experiments to elucidate the strengths and weakenesses of the RKS test versus the more traditional kernel MMD test.

Sudakov-Fernique post-AMP, and a new proof of the local convexity of the TAP free energy

In many problems in modern statistics and machine learning, it is often of interest to establish that a first order method on a non-convex risk function eventually enters a region of parameter space in which the risk is locally convex. We derive an asymptotic comparison inequality, which we call the Sudakov-Fernique post-AMP inequality, which, in a certain class of problems involving a GOE matrix, is able to probe properties of an optimization landscape locally around the iterates of an approximate message passing (AMP) algorithm. As an example of its use, we provide a new, and arguably simpler, proof of some of the results of Celentano et al. (2021), which establishes that the so-called TAP free energy in the $\mathbb{Z}_2$-synchronization problem is locally convex in the region to which AMP converges. We further prove a conjecture of El Alaoui et al. (2022) involving the local convexity of a related but distinct TAP free energy, which, as a consequence, confirms that their algorithm efficiently samples from the Sherrington-Kirkpatrick Gibbs measure throughout the "easy" regime.

Local convexity of the TAP free energy and AMP convergence for Z2-synchronization

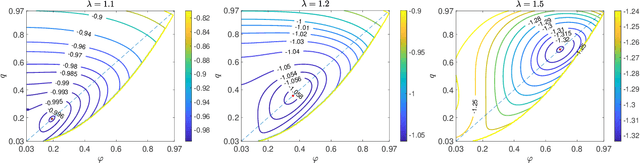
We study mean-field variational Bayesian inference using the TAP approach, for Z2-synchronization as a prototypical example of a high-dimensional Bayesian model. We show that for any signal strength $\lambda > 1$ (the weak-recovery threshold), there exists a unique local minimizer of the TAP free energy functional near the mean of the Bayes posterior law. Furthermore, the TAP free energy in a local neighborhood of this minimizer is strongly convex. Consequently, a natural-gradient/mirror-descent algorithm achieves linear convergence to this minimizer from a local initialization, which may be obtained by a finite number of iterates of Approximate Message Passing (AMP). This provides a rigorous foundation for variational inference in high dimensions via minimization of the TAP free energy. We also analyze the finite-sample convergence of AMP, showing that AMP is asymptotically stable at the TAP minimizer for any $\lambda > 1$, and is linearly convergent to this minimizer from a spectral initialization for sufficiently large $\lambda$. Such a guarantee is stronger than results obtainable by state evolution analyses, which only describe a fixed number of AMP iterations in the infinite-sample limit. Our proofs combine the Kac-Rice formula and Sudakov-Fernique Gaussian comparison inequality to analyze the complexity of critical points that satisfy strong convexity and stability conditions within their local neighborhoods.

Minimum complexity interpolation in random features models

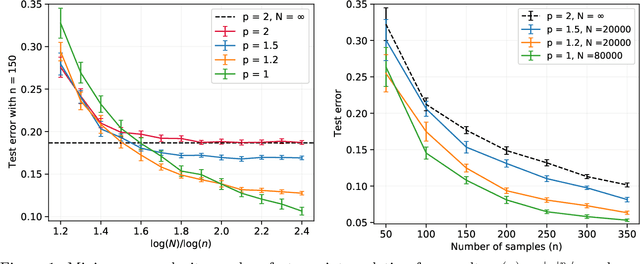
Despite their many appealing properties, kernel methods are heavily affected by the curse of dimensionality. For instance, in the case of inner product kernels in $\mathbb{R}^d$, the Reproducing Kernel Hilbert Space (RKHS) norm is often very large for functions that depend strongly on a small subset of directions (ridge functions). Correspondingly, such functions are difficult to learn using kernel methods. This observation has motivated the study of generalizations of kernel methods, whereby the RKHS norm -- which is equivalent to a weighted $\ell_2$ norm -- is replaced by a weighted functional $\ell_p$ norm, which we refer to as $\mathcal{F}_p$ norm. Unfortunately, tractability of these approaches is unclear. The kernel trick is not available and minimizing these norms requires to solve an infinite-dimensional convex problem. We study random features approximations to these norms and show that, for $p>1$, the number of random features required to approximate the original learning problem is upper bounded by a polynomial in the sample size. Hence, learning with $\mathcal{F}_p$ norms is tractable in these cases. We introduce a proof technique based on uniform concentration in the dual, which can be of broader interest in the study of overparametrized models.

The Lasso with general Gaussian designs with applications to hypothesis testing

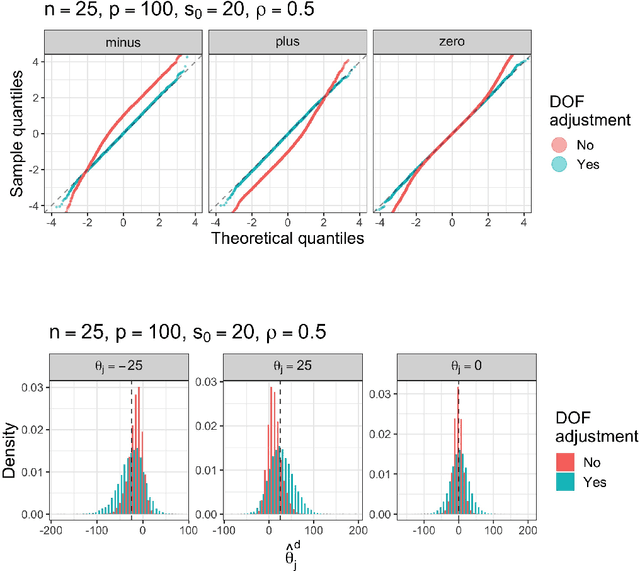
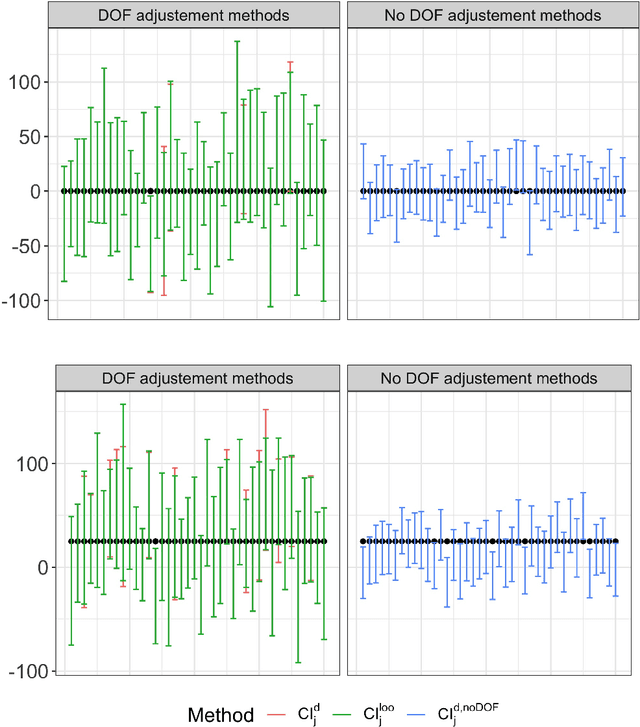
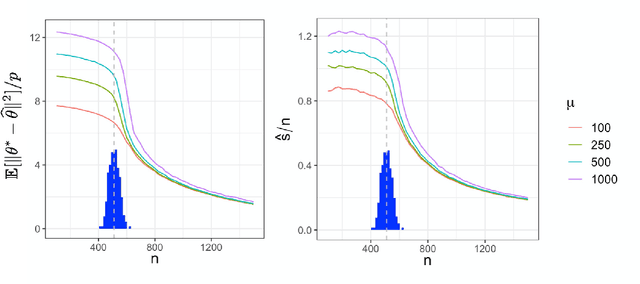
The Lasso is a method for high-dimensional regression, which is now commonly used when the number of covariates $p$ is of the same order or larger than the number of observations $n$. Classical asymptotic normality theory is not applicable for this model due to two fundamental reasons: $(1)$ The regularized risk is non-smooth; $(2)$ The distance between the estimator $\bf \widehat{\theta}$ and the true parameters vector $\bf \theta^\star$ cannot be neglected. As a consequence, standard perturbative arguments that are the traditional basis for asymptotic normality fail. On the other hand, the Lasso estimator can be precisely characterized in the regime in which both $n$ and $p$ are large, while $n/p$ is of order one. This characterization was first obtained in the case of standard Gaussian designs, and subsequently generalized to other high-dimensional estimation procedures. Here we extend the same characterization to Gaussian correlated designs with non-singular covariance structure. This characterization is expressed in terms of a simpler ``fixed design'' model. We establish non-asymptotic bounds on the distance between distributions of various quantities in the two models, which hold uniformly over signals $\bf \theta^\star$ in a suitable sparsity class, and values of the regularization parameter. As applications, we study the distribution of the debiased Lasso, and show that a degrees-of-freedom correction is necessary for computing valid confidence intervals.

The estimation error of general first order methods

Modern large-scale statistical models require to estimate thousands to millions of parameters. This is often accomplished by iterative algorithms such as gradient descent, projected gradient descent or their accelerated versions. What are the fundamental limits to these approaches? This question is well understood from an optimization viewpoint when the underlying objective is convex. Work in this area characterizes the gap to global optimality as a function of the number of iterations. However, these results have only indirect implications in terms of the gap to statistical optimality. Here we consider two families of high-dimensional estimation problems: high-dimensional regression and low-rank matrix estimation, and introduce a class of `general first order methods' that aim at efficiently estimating the underlying parameters. This class of algorithms is broad enough to include classical first order optimization (for convex and non-convex objectives), but also other types of algorithms. Under a random design assumption, we derive lower bounds on the estimation error that hold in the high-dimensional asymptotics in which both the number of observations and the number of parameters diverge. These lower bounds are optimal in the sense that there exist algorithms whose estimation error matches the lower bounds up to asymptotically negligible terms. We illustrate our general results through applications to sparse phase retrieval and sparse principal component analysis.