Gradient Equilibrium in Online Learning: Theory and Applications

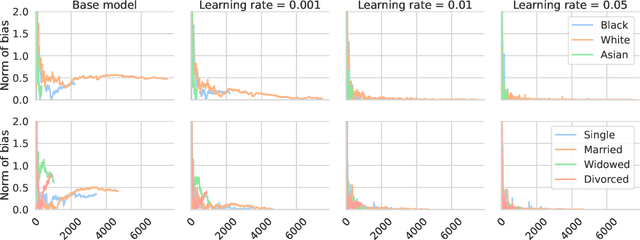
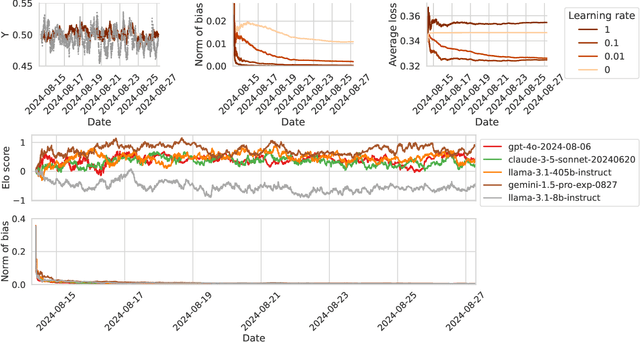
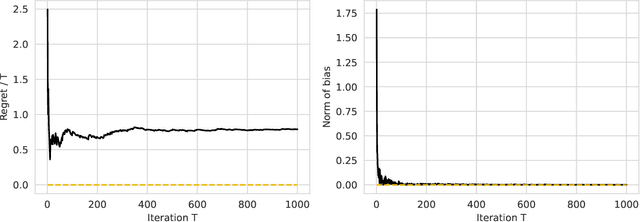
We present a new perspective on online learning that we refer to as gradient equilibrium: a sequence of iterates achieves gradient equilibrium if the average of gradients of losses along the sequence converges to zero. In general, this condition is not implied by nor implies sublinear regret. It turns out that gradient equilibrium is achievable by standard online learning methods such as gradient descent and mirror descent with constant step sizes (rather than decaying step sizes, as is usually required for no regret). Further, as we show through examples, gradient equilibrium translates into an interpretable and meaningful property in online prediction problems spanning regression, classification, quantile estimation, and others. Notably, we show that the gradient equilibrium framework can be used to develop a debiasing scheme for black-box predictions under arbitrary distribution shift, based on simple post hoc online descent updates. We also show that post hoc gradient updates can be used to calibrate predicted quantiles under distribution shift, and that the framework leads to unbiased Elo scores for pairwise preference prediction.

Revisiting Optimism and Model Complexity in the Wake of Overparameterized Machine Learning

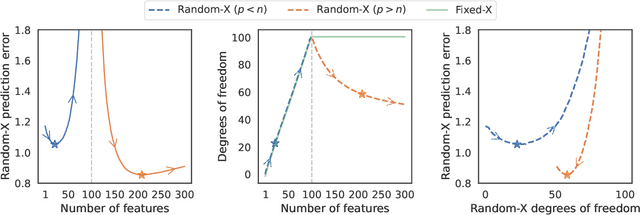
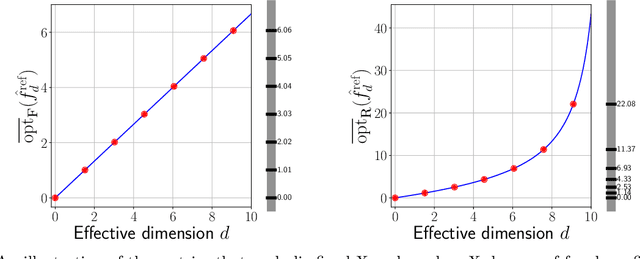
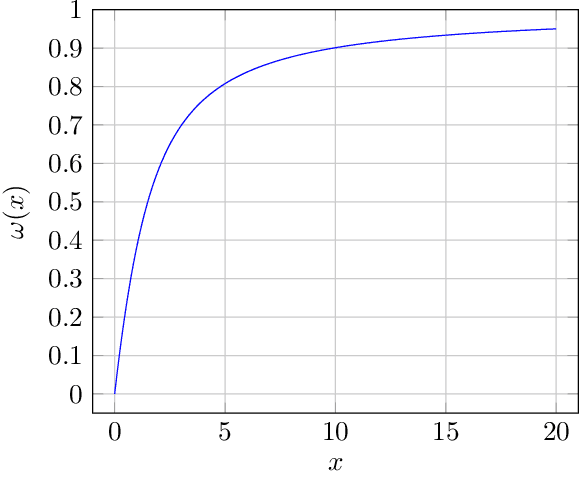
Common practice in modern machine learning involves fitting a large number of parameters relative to the number of observations. These overparameterized models can exhibit surprising generalization behavior, e.g., ``double descent'' in the prediction error curve when plotted against the raw number of model parameters, or another simplistic notion of complexity. In this paper, we revisit model complexity from first principles, by first reinterpreting and then extending the classical statistical concept of (effective) degrees of freedom. Whereas the classical definition is connected to fixed-X prediction error (in which prediction error is defined by averaging over the same, nonrandom covariate points as those used during training), our extension of degrees of freedom is connected to random-X prediction error (in which prediction error is averaged over a new, random sample from the covariate distribution). The random-X setting more naturally embodies modern machine learning problems, where highly complex models, even those complex enough to interpolate the training data, can still lead to desirable generalization performance under appropriate conditions. We demonstrate the utility of our proposed complexity measures through a mix of conceptual arguments, theory, and experiments, and illustrate how they can be used to interpret and compare arbitrary prediction models.

Optimal Ridge Regularization for Out-of-Distribution Prediction

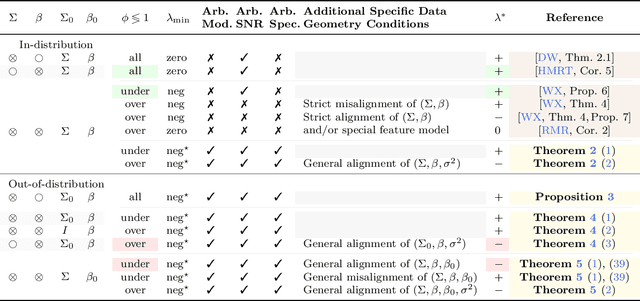
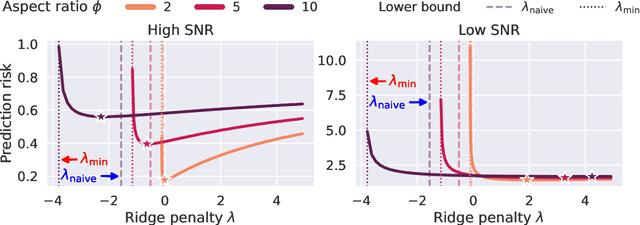
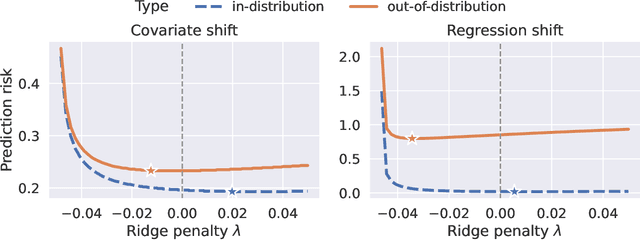
We study the behavior of optimal ridge regularization and optimal ridge risk for out-of-distribution prediction, where the test distribution deviates arbitrarily from the train distribution. We establish general conditions that determine the sign of the optimal regularization level under covariate and regression shifts. These conditions capture the alignment between the covariance and signal structures in the train and test data and reveal stark differences compared to the in-distribution setting. For example, a negative regularization level can be optimal under covariate shift or regression shift, even when the training features are isotropic or the design is underparameterized. Furthermore, we prove that the optimally-tuned risk is monotonic in the data aspect ratio, even in the out-of-distribution setting and when optimizing over negative regularization levels. In general, our results do not make any modeling assumptions for the train or the test distributions, except for moment bounds, and allow for arbitrary shifts and the widest possible range of (negative) regularization levels.

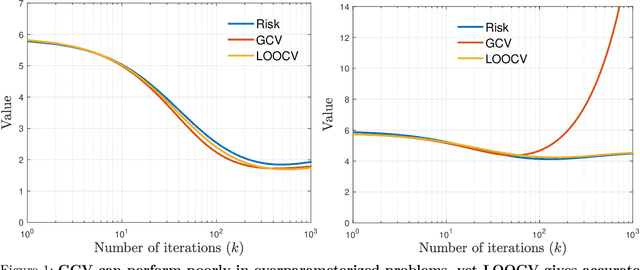
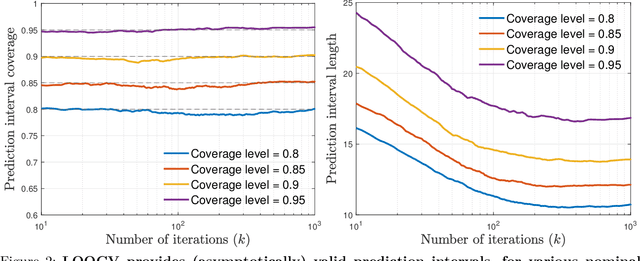
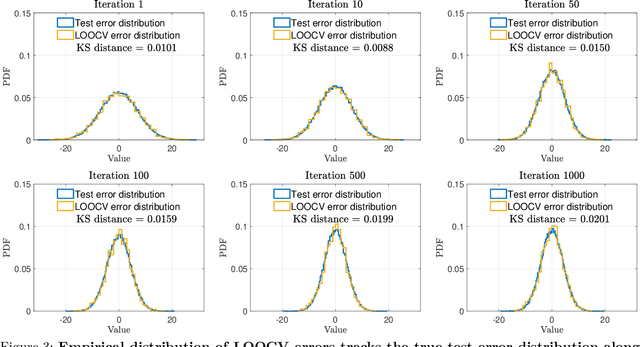
Failures and Successes of Cross-Validation for Early-Stopped Gradient Descent

We analyze the statistical properties of generalized cross-validation (GCV) and leave-one-out cross-validation (LOOCV) applied to early-stopped gradient descent (GD) in high-dimensional least squares regression. We prove that GCV is generically inconsistent as an estimator of the prediction risk of early-stopped GD, even for a well-specified linear model with isotropic features. In contrast, we show that LOOCV converges uniformly along the GD trajectory to the prediction risk. Our theory requires only mild assumptions on the data distribution and does not require the underlying regression function to be linear. Furthermore, by leveraging the individual LOOCV errors, we construct consistent estimators for the entire prediction error distribution along the GD trajectory and consistent estimators for a wide class of error functionals. This in particular enables the construction of pathwise prediction intervals based on GD iterates that have asymptotically correct nominal coverage conditional on the training data.

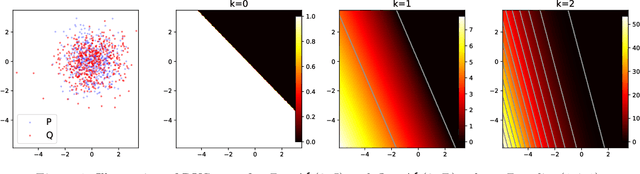
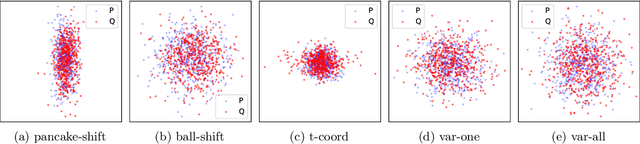
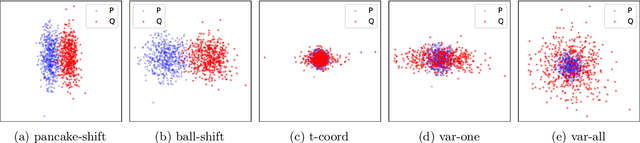
Maximum Mean Discrepancy Meets Neural Networks: The Radon-Kolmogorov-Smirnov Test

Maximum mean discrepancy (MMD) refers to a general class of nonparametric two-sample tests that are based on maximizing the mean difference over samples from one distribution $P$ versus another $Q$, over all choices of data transformations $f$ living in some function space $\mathcal{F}$. Inspired by recent work that connects what are known as functions of $\textit{Radon bounded variation}$ (RBV) and neural networks (Parhi and Nowak, 2021, 2023), we study the MMD defined by taking $\mathcal{F}$ to be the unit ball in the RBV space of a given smoothness order $k \geq 0$. This test, which we refer to as the $\textit{Radon-Kolmogorov-Smirnov}$ (RKS) test, can be viewed as a generalization of the well-known and classical Kolmogorov-Smirnov (KS) test to multiple dimensions and higher orders of smoothness. It is also intimately connected to neural networks: we prove that the witness in the RKS test -- the function $f$ achieving the maximum mean difference -- is always a ridge spline of degree $k$, i.e., a single neuron in a neural network. This allows us to leverage the power of modern deep learning toolkits to (approximately) optimize the criterion that underlies the RKS test. We prove that the RKS test has asymptotically full power at distinguishing any distinct pair $P \not= Q$ of distributions, derive its asymptotic null distribution, and carry out extensive experiments to elucidate the strengths and weakenesses of the RKS test versus the more traditional kernel MMD test.

Conformal PID Control for Time Series Prediction

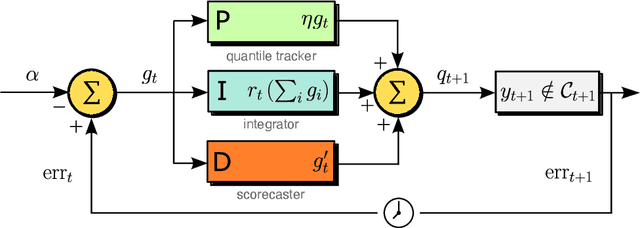
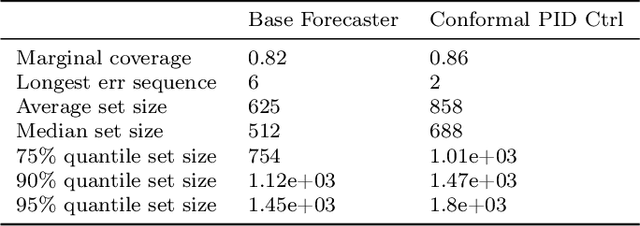
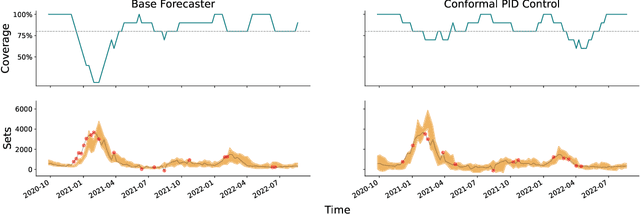
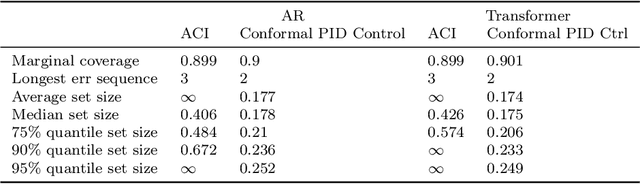
We study the problem of uncertainty quantification for time series prediction, with the goal of providing easy-to-use algorithms with formal guarantees. The algorithms we present build upon ideas from conformal prediction and control theory, are able to prospectively model conformal scores in an online setting, and adapt to the presence of systematic errors due to seasonality, trends, and general distribution shifts. Our theory both simplifies and strengthens existing analyses in online conformal prediction. Experiments on 4-week-ahead forecasting of statewide COVID-19 death counts in the U.S. show an improvement in coverage over the ensemble forecaster used in official CDC communications. We also run experiments on predicting electricity demand, market returns, and temperature using autoregressive, Theta, Prophet, and Transformer models. We provide an extendable codebase for testing our methods and for the integration of new algorithms, data sets, and forecasting rules.

Class-Conditional Conformal Prediction With Many Classes

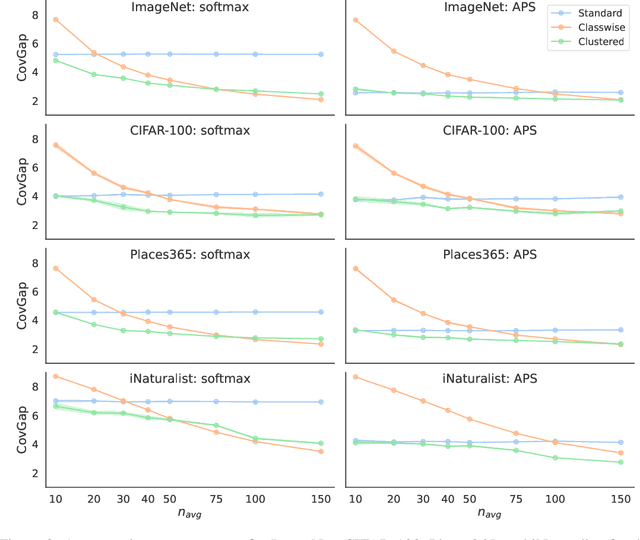
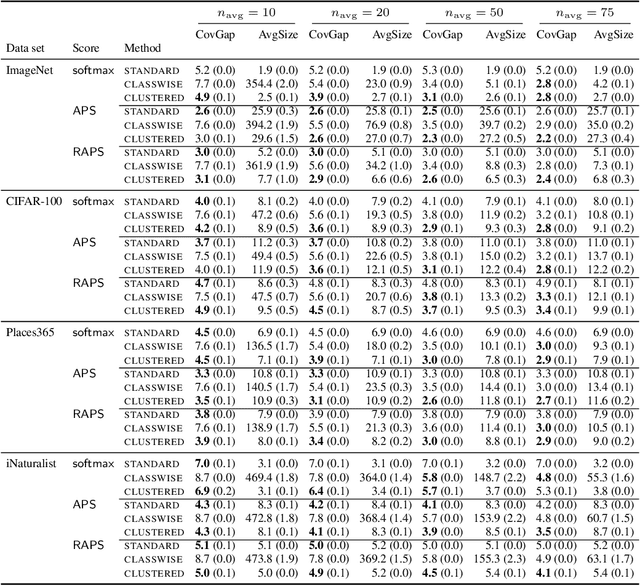
Standard conformal prediction methods provide a marginal coverage guarantee, which means that for a random test point, the conformal prediction set contains the true label with a user-chosen probability. In many classification problems, we would like to obtain a stronger guarantee -- that for test points of a specific class, the prediction set contains the true label with the same user-chosen probability. Existing conformal prediction methods do not work well when there is a limited amount of labeled data per class, as is often the case in real applications where the number of classes is large. We propose a method called clustered conformal prediction, which clusters together classes that have "similar" conformal scores and then performs conformal prediction at the cluster level. Based on empirical evaluation across four image data sets with many (up to 1000) classes, we find that clustered conformal typically outperforms existing methods in terms of class-conditional coverage and set size metrics.

The Voronoigram: Minimax Estimation of Bounded Variation Functions From Scattered Data

We consider the problem of estimating a multivariate function $f_0$ of bounded variation (BV), from noisy observations $y_i = f_0(x_i) + z_i$ made at random design points $x_i \in \mathbb{R}^d$, $i=1,\ldots,n$. We study an estimator that forms the Voronoi diagram of the design points, and then solves an optimization problem that regularizes according to a certain discrete notion of total variation (TV): the sum of weighted absolute differences of parameters $\theta_i,\theta_j$ (which estimate the function values $f_0(x_i),f_0(x_j)$) at all neighboring cells $i,j$ in the Voronoi diagram. This is seen to be equivalent to a variational optimization problem that regularizes according to the usual continuum (measure-theoretic) notion of TV, once we restrict the domain to functions that are piecewise constant over the Voronoi diagram. The regression estimator under consideration hence performs (shrunken) local averaging over adaptively formed unions of Voronoi cells, and we refer to it as the Voronoigram, following the ideas in Koenker (2005), and drawing inspiration from Tukey's regressogram (Tukey, 1961). Our contributions in this paper span both the conceptual and theoretical frontiers: we discuss some of the unique properties of the Voronoigram in comparison to TV-regularized estimators that use other graph-based discretizations; we derive the asymptotic limit of the Voronoi TV functional; and we prove that the Voronoigram is minimax rate optimal (up to log factors) for estimating BV functions that are essentially bounded.

Multivariate Trend Filtering for Lattice Data

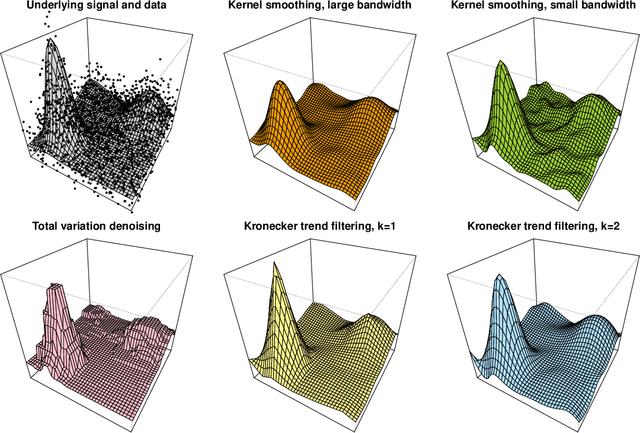
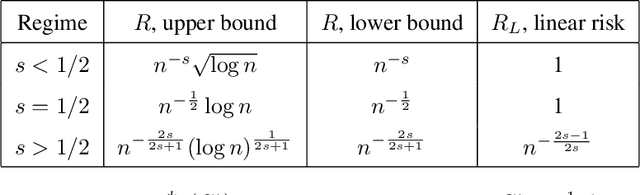
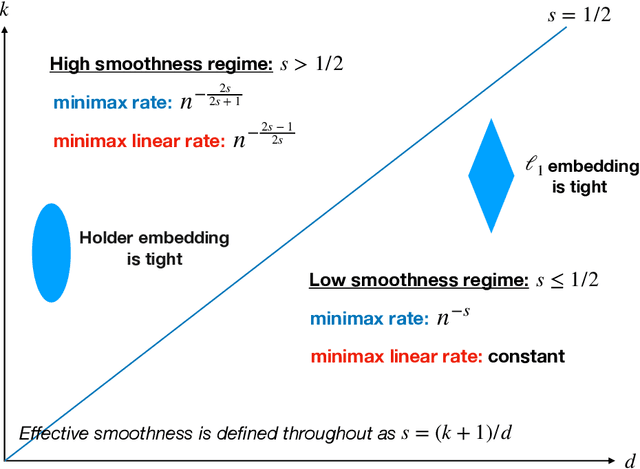
We study a multivariate version of trend filtering, called Kronecker trend filtering or KTF, for the case in which the design points form a lattice in $d$ dimensions. KTF is a natural extension of univariate trend filtering (Steidl et al., 2006; Kim et al., 2009; Tibshirani, 2014), and is defined by minimizing a penalized least squares problem whose penalty term sums the absolute (higher-order) differences of the parameter to be estimated along each of the coordinate directions. The corresponding penalty operator can be written in terms of Kronecker products of univariate trend filtering penalty operators, hence the name Kronecker trend filtering. Equivalently, one can view KTF in terms of an $\ell_1$-penalized basis regression problem where the basis functions are tensor products of falling factorial functions, a piecewise polynomial (discrete spline) basis that underlies univariate trend filtering. This paper is a unification and extension of the results in Sadhanala et al. (2016, 2017). We develop a complete set of theoretical results that describe the behavior of $k^{\mathrm{th}}$ order Kronecker trend filtering in $d$ dimensions, for every $k \geq 0$ and $d \geq 1$. This reveals a number of interesting phenomena, including the dominance of KTF over linear smoothers in estimating heterogeneously smooth functions, and a phase transition at $d=2(k+1)$, a boundary past which (on the high dimension-to-smoothness side) linear smoothers fail to be consistent entirely. We also leverage recent results on discrete splines from Tibshirani (2020), in particular, discrete spline interpolation results that enable us to extend the KTF estimate to any off-lattice location in constant-time (independent of the size of the lattice $n$).

Recalibrating probabilistic forecasts of epidemics

Distributional forecasts are important for a wide variety of applications, including forecasting epidemics. Often, forecasts are miscalibrated, or unreliable in assigning uncertainty to future events. We present a recalibration method that can be applied to a black-box forecaster given retrospective forecasts and observations, as well as an extension to make this method more effective in recalibrating epidemic forecasts. This method is guaranteed to improve calibration and log score performance when trained and measured in-sample. We also prove that the increase in expected log score of a recalibrated forecaster is equal to the entropy of the PIT distribution. We apply this recalibration method to the 27 influenza forecasters in the FluSight Network and show that recalibration reliably improves forecast accuracy and calibration. This method is effective, robust, and easy to use as a post-processing tool to improve epidemic forecasts.