Learnable Chernoff Baselines for Inference-Time Alignment

We study inference-time reward-guided alignment for generative models. Existing methods often rely on either architecture-specific adaptations or computationally costly inference procedures. We introduce Learnable Chernoff Baselines (LCBs) as a method for efficiently and approximately sampling from the exponentially tilted kernels that arise from KL-regularized reward alignment. Using only black-box sampling access to the pretrained model, LCBs implement a form of rejection sampling with adaptively selected acceptance probabilities, which allows fine-grained control over inference-compute scaling. We establish total-variation guarantees to the ideal aligned model, and demonstrate in both continuous and discrete diffusion settings that LCB sampling closely matches ideal rejection sampling while using substantially fewer queries to the pretrained model.

A second order regret bound for NormalHedge

We consider the problem of prediction with expert advice for ``easy'' sequences. We show that a variant of NormalHedge enjoys a second-order $ε$-quantile regret bound of $O\big(\sqrt{V_T \log(V_T/ε)}\big) $ when $V_T > \log N$, where $V_T$ is the cumulative second moment of instantaneous per-expert regret averaged with respect to a natural distribution determined by the algorithm. The algorithm is motivated by a continuous time limit using Stochastic Differential Equations. The discrete time analysis uses self-concordance techniques.

ConvexBench: Can LLMs Recognize Convex Functions?

Convex analysis is a modern branch of mathematics with many applications. As Large Language Models (LLMs) start to automate research-level math and sciences, it is important for LLMs to demonstrate the ability to understand and reason with convexity. We introduce \cb, a scalable and mechanically verifiable benchmark for testing \textit{whether LLMs can identify the convexity of a symbolic objective under deep functional composition.} Experiments on frontier LLMs reveal a sharp compositional reasoning gap: performance degrades rapidly with increasing depth, dropping from an F1-score of $1.0$ at depth $2$ to approximately $0.2$ at depth $100$. Inspection of models' reasoning traces indicates two failure modes: \textit{parsing failure} and \textit{lazy reasoning}. To address these limitations, we propose an agentic divide-and-conquer framework that (i) offloads parsing to an external tool to construct an abstract syntax tree (AST) and (ii) enforces recursive reasoning over each intermediate sub-expression with focused context. This framework reliably mitigates deep-composition failures, achieving substantial performance improvement at large depths (e.g., F1-Score $= 1.0$ at depth $100$).

Private-RAG: Answering Multiple Queries with LLMs while Keeping Your Data Private

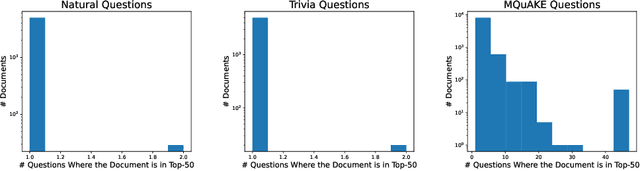
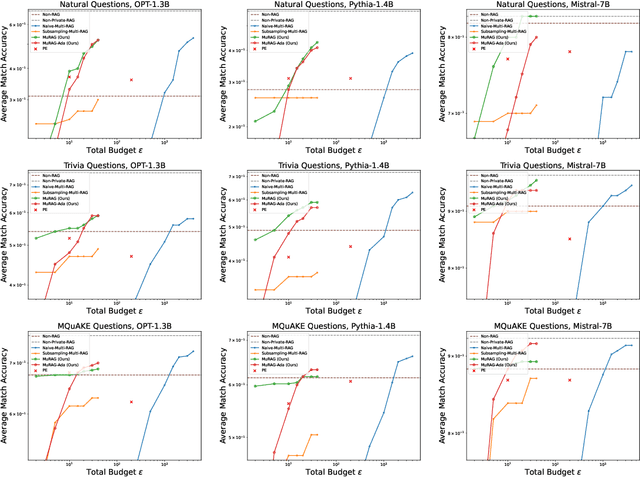
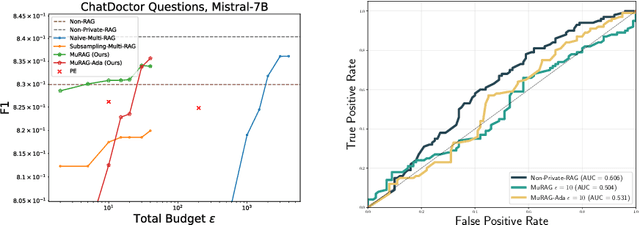
Retrieval-augmented generation (RAG) enhances large language models (LLMs) by retrieving documents from an external corpus at inference time. When this corpus contains sensitive information, however, unprotected RAG systems are at risk of leaking private information. Prior work has introduced differential privacy (DP) guarantees for RAG, but only in single-query settings, which fall short of realistic usage. In this paper, we study the more practical multi-query setting and propose two DP-RAG algorithms. The first, MURAG, leverages an individual privacy filter so that the accumulated privacy loss only depends on how frequently each document is retrieved rather than the total number of queries. The second, MURAG-ADA, further improves utility by privately releasing query-specific thresholds, enabling more precise selection of relevant documents. Our experiments across multiple LLMs and datasets demonstrate that the proposed methods scale to hundreds of queries within a practical DP budget ($\varepsilon\approx10$), while preserving meaningful utility.

Stable Minima of ReLU Neural Networks Suffer from the Curse of Dimensionality: The Neural Shattering Phenomenon

We study the implicit bias of flatness / low (loss) curvature and its effects on generalization in two-layer overparameterized ReLU networks with multivariate inputs -- a problem well motivated by the minima stability and edge-of-stability phenomena in gradient-descent training. Existing work either requires interpolation or focuses only on univariate inputs. This paper presents new and somewhat surprising theoretical results for multivariate inputs. On two natural settings (1) generalization gap for flat solutions, and (2) mean-squared error (MSE) in nonparametric function estimation by stable minima, we prove upper and lower bounds, which establish that while flatness does imply generalization, the resulting rates of convergence necessarily deteriorate exponentially as the input dimension grows. This gives an exponential separation between the flat solutions vis-\`a-vis low-norm solutions (i.e., weight decay), which knowingly do not suffer from the curse of dimensionality. In particular, our minimax lower bound construction, based on a novel packing argument with boundary-localized ReLU neurons, reveals how flat solutions can exploit a kind of ''neural shattering'' where neurons rarely activate, but with high weight magnitudes. This leads to poor performance in high dimensions. We corroborate these theoretical findings with extensive numerical simulations. To the best of our knowledge, our analysis provides the first systematic explanation for why flat minima may fail to generalize in high dimensions.

Adapting to Linear Separable Subsets with Large-Margin in Differentially Private Learning

This paper studies the problem of differentially private empirical risk minimization (DP-ERM) for binary linear classification. We obtain an efficient $(\varepsilon,\delta)$-DP algorithm with an empirical zero-one risk bound of $\tilde{O}\left(\frac{1}{\gamma^2\varepsilon n} + \frac{|S_{\mathrm{out}}|}{\gamma n}\right)$ where $n$ is the number of data points, $S_{\mathrm{out}}$ is an arbitrary subset of data one can remove and $\gamma$ is the margin of linear separation of the remaining data points (after $S_{\mathrm{out}}$ is removed). Here, $\tilde{O}(\cdot)$ hides only logarithmic terms. In the agnostic case, we improve the existing results when the number of outliers is small. Our algorithm is highly adaptive because it does not require knowing the margin parameter $\gamma$ or outlier subset $S_{\mathrm{out}}$. We also derive a utility bound for the advanced private hyperparameter tuning algorithm.

Adaptive Estimation and Learning under Temporal Distribution Shift

In this paper, we study the problem of estimation and learning under temporal distribution shift. Consider an observation sequence of length $n$, which is a noisy realization of a time-varying groundtruth sequence. Our focus is to develop methods to estimate the groundtruth at the final time-step while providing sharp point-wise estimation error rates. We show that, without prior knowledge on the level of temporal shift, a wavelet soft-thresholding estimator provides an optimal estimation error bound for the groundtruth. Our proposed estimation method generalizes existing researches Mazzetto and Upfal (2023) by establishing a connection between the sequence's non-stationarity level and the sparsity in the wavelet-transformed domain. Our theoretical findings are validated by numerical experiments. Additionally, we applied the estimator to derive sparsity-aware excess risk bounds for binary classification under distribution shift and to develop computationally efficient training objectives. As a final contribution, we draw parallels between our results and the classical signal processing problem of total-variation denoising (Mammen and van de Geer,1997; Tibshirani, 2014), uncovering novel optimal algorithms for such task.

Adapting to Online Distribution Shifts in Deep Learning: A Black-Box Approach

We study the well-motivated problem of online distribution shift in which the data arrive in batches and the distribution of each batch can change arbitrarily over time. Since the shifts can be large or small, abrupt or gradual, the length of the relevant historical data to learn from may vary over time, which poses a major challenge in designing algorithms that can automatically adapt to the best ``attention span'' while remaining computationally efficient. We propose a meta-algorithm that takes any network architecture and any Online Learner (OL) algorithm as input and produces a new algorithm which provably enhances the performance of the given OL under non-stationarity. Our algorithm is efficient (it requires maintaining only $O(\log(T))$ OL instances) and adaptive (it automatically chooses OL instances with the ideal ``attention'' length at every timestamp). Experiments on various real-world datasets across text and image modalities show that our method consistently improves the accuracy of user specified OL algorithms for classification tasks. Key novel algorithmic ingredients include a \emph{multi-resolution instance} design inspired by wavelet theory and a cross-validation-through-time technique. Both could be of independent interest.

Purifying Approximate Differential Privacy with Randomized Post-processing

We propose a framework to convert $(\varepsilon, \delta)$-approximate Differential Privacy (DP) mechanisms into $(\varepsilon, 0)$-pure DP mechanisms, a process we call ``purification''. This algorithmic technique leverages randomized post-processing with calibrated noise to eliminate the $\delta$ parameter while preserving utility. By combining the tighter utility bounds and computational efficiency of approximate DP mechanisms with the stronger guarantees of pure DP, our approach achieves the best of both worlds. We illustrate the applicability of this framework in various settings, including Differentially Private Empirical Risk Minimization (DP-ERM), data-dependent DP mechanisms such as Propose-Test-Release (PTR), and query release tasks. To the best of our knowledge, this is the first work to provide a systematic method for transforming approximate DP into pure DP while maintaining competitive accuracy and computational efficiency.

Dynamic Pricing with Adversarially-Censored Demands

We study an online dynamic pricing problem where the potential demand at each time period $t=1,2,\ldots, T$ is stochastic and dependent on the price. However, a perishable inventory is imposed at the beginning of each time $t$, censoring the potential demand if it exceeds the inventory level. To address this problem, we introduce a pricing algorithm based on the optimistic estimates of derivatives. We show that our algorithm achieves $\tilde{O}(\sqrt{T})$ optimal regret even with adversarial inventory series. Our findings advance the state-of-the-art in online decision-making problems with censored feedback, offering a theoretically optimal solution against adversarial observations.