Modular Layout Synthesis (MLS): Front-end Code via Structure Normalization and Constrained Generation

Automated front-end engineering drastically reduces development cycles and minimizes manual coding overhead. While Generative AI has shown promise in translating designs to code, current solutions often produce monolithic scripts, failing to natively support modern ecosystems like React, Vue, or Angular. Furthermore, the generated code frequently suffers from poor modularity, making it difficult to maintain. To bridge this gap, we introduce Modular Layout Synthesis (MLS), a hierarchical framework that merges visual understanding with structural normalization. Initially, a visual-semantic encoder maps the screen capture into a serialized tree topology, capturing the essential layout hierarchy. Instead of simple parsing, we apply heuristic deduplication and pattern recognition to isolate reusable blocks, creating a framework-agnostic schema. Finally, a constraint-based generation protocol guides the LLM to synthesize production-ready code with strict typing and component props. Evaluations show that MLS significantly outperforms existing baselines, ensuring superior code reusability and structural integrity across multiple frameworks

MiVLA: Towards Generalizable Vision-Language-Action Model with Human-Robot Mutual Imitation Pre-training

While leveraging abundant human videos and simulated robot data poses a scalable solution to the scarcity of real-world robot data, the generalization capability of existing vision-language-action models (VLAs) remains limited by mismatches in camera views, visual appearance, and embodiment morphologies. To overcome this limitation, we propose MiVLA, a generalizable VLA empowered by human-robot mutual imitation pre-training, which leverages inherent behavioral similarity between human hands and robotic arms to build a foundation of strong behavioral priors for both human actions and robotic control. Specifically, our method utilizes kinematic rules with left/right hand coordinate systems for bidirectional alignment between human and robot action spaces. Given human or simulated robot demonstrations, MiVLA is trained to forecast behavior trajectories for one embodiment, and imitate behaviors for another one unseen in the demonstration. Based on this mutual imitation, it integrates the behavioral fidelity of real-world human data with the manipulative diversity of simulated robot data into a unified model, thereby enhancing the generalization capability for downstream tasks. Extensive experiments conducted on both simulation and real-world platforms with three robots (ARX, PiPer and LocoMan), demonstrate that MiVLA achieves strong improved generalization capability, outperforming state-of-the-art VLAs (e.g., $\boldsymbolπ_{0}$, $\boldsymbolπ_{0.5}$ and H-RDT) by 25% in simulation, and 14% in real-world robot control tasks.

Bayesian Optimization with Inexact Acquisition: Is Random Grid Search Sufficient?

Bayesian optimization (BO) is a widely used iterative algorithm for optimizing black-box functions. Each iteration requires maximizing an acquisition function, such as the upper confidence bound (UCB) or a sample path from the Gaussian process (GP) posterior, as in Thompson sampling (TS). However, finding an exact solution to these maximization problems is often intractable and computationally expensive. Reflecting such realistic situations, in this paper, we delve into the effect of inexact maximizers of the acquisition functions. Defining a measure of inaccuracy in acquisition solutions, we establish cumulative regret bounds for both GP-UCB and GP-TS without requiring exact solutions of acquisition function maximization. Our results show that under appropriate conditions on accumulated inaccuracy, inexact BO algorithms can still achieve sublinear cumulative regret. Motivated by such findings, we provide both theoretical justification and numerical validation for random grid search as an effective and computationally efficient acquisition function solver.

PoseX: AI Defeats Physics Approaches on Protein-Ligand Cross Docking

Recently, significant progress has been made in protein-ligand docking, especially in modern deep learning methods, and some benchmarks were proposed, e.g., PoseBench, Plinder. However, these benchmarks suffer from less practical evaluation setups (e.g., blind docking, self docking), or heavy framework that involves training, raising challenges to assess docking methods efficiently. To fill this gap, we proposed PoseX, an open-source benchmark focusing on self-docking and cross-docking, to evaluate the algorithmic advances practically and comprehensively. Specifically, first, we curate a new evaluation dataset with 718 entries for self docking and 1,312 for cross docking; second, we incorporate 22 docking methods across three methodological categories, including (1) traditional physics-based methods (e.g., Schr\"odinger Glide), (2) AI docking methods (e.g., DiffDock), (3) AI co-folding methods (e.g., AlphaFold3); third, we design a relaxation method as post-processing to minimize conformation energy and refine binding pose; fourth, we released a leaderboard to rank submitted models in real time. We draw some key insights via extensive experiments: (1) AI-based approaches have already surpassed traditional physics-based approaches in overall docking accuracy (RMSD). The longstanding generalization issues that have plagued AI molecular docking have been significantly alleviated in the latest models. (2) The stereochemical deficiencies of AI-based approaches can be greatly alleviated with post-processing relaxation. Combining AI docking methods with the enhanced relaxation method achieves the best performance to date. (3) AI co-folding methods commonly face ligand chirality issues, which cannot be resolved by relaxation. The code, curated dataset and leaderboard are released at https://github.com/CataAI/PoseX.

Quantum Non-Linear Bandit Optimization

We study non-linear bandit optimization where the learner maximizes a black-box function with zeroth order function oracle, which has been successfully applied in many critical applications such as drug discovery and hyperparameter tuning. Existing works have showed that with the aid of quantum computing, it is possible to break the $\Omega(\sqrt{T})$ regret lower bound in classical settings and achieve the new $O(\mathrm{poly}\log T)$ upper bound. However, they usually assume that the objective function sits within the reproducing kernel Hilbert space and their algorithms suffer from the curse of dimensionality. In this paper, we propose the new Q-NLB-UCB algorithm which uses the novel parametric function approximation technique and enjoys performance improvement due to quantum fast-forward and quantum Monte Carlo mean estimation. We prove that the regret bound of Q-NLB-UCB is not only $O(\mathrm{poly}\log T)$ but also input dimension-free, making it applicable for high-dimensional tasks. At the heart of our analyses are a new quantum regression oracle and a careful construction of parameter uncertainty region. Our algorithm is also validated for its efficiency on both synthetic and real-world tasks.

ME-CPT: Multi-Task Enhanced Cross-Temporal Point Transformer for Urban 3D Change Detection

The point clouds collected by the Airborne Laser Scanning (ALS) system provide accurate 3D information of urban land covers. By utilizing multi-temporal ALS point clouds, semantic changes in urban area can be captured, demonstrating significant potential in urban planning, emergency management, and infrastructure maintenance. Existing 3D change detection methods struggle to efficiently extract multi-class semantic information and change features, still facing the following challenges: (1) the difficulty of accurately modeling cross-temporal point clouds spatial relationships for effective change feature extraction; (2) class imbalance of change samples which hinders distinguishability of semantic features; (3) the lack of real-world datasets for 3D semantic change detection. To resolve these challenges, we propose the Multi-task Enhanced Cross-temporal Point Transformer (ME-CPT) network. ME-CPT establishes spatiotemporal correspondences between point cloud across different epochs and employs attention mechanisms to jointly extract semantic change features, facilitating information exchange and change comparison. Additionally, we incorporate a semantic segmentation task and through the multi-task training strategy, further enhance the distinguishability of semantic features, reducing the impact of class imbalance in change types. Moreover, we release a 22.5 $km^2$ 3D semantic change detection dataset, offering diverse scenes for comprehensive evaluation. Experiments on multiple datasets show that the proposed MT-CPT achieves superior performance compared to existing state-of-the-art methods. The source code and dataset will be released upon acceptance at \url{https://github.com/zhangluqi0209/ME-CPT}.

No-Regret Linear Bandits under Gap-Adjusted Misspecification

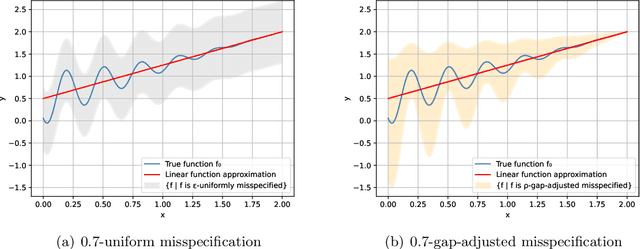
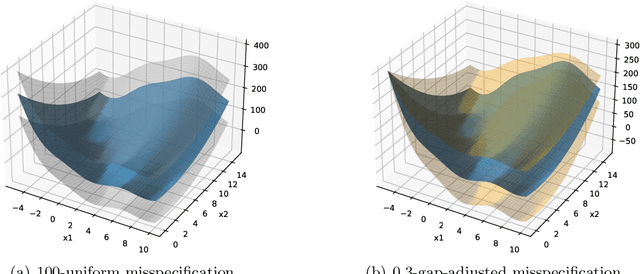
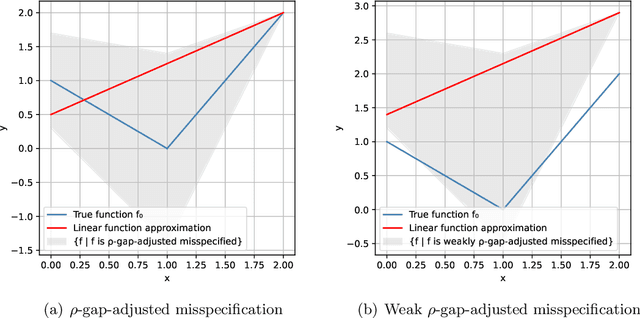
This work studies linear bandits under a new notion of gap-adjusted misspecification and is an extension of Liu et al. (2023). When the underlying reward function is not linear, existing linear bandits work usually relies on a uniform misspecification parameter $\epsilon$ that measures the sup-norm error of the best linear approximation. This results in an unavoidable linear regret whenever $\epsilon > 0$. We propose a more natural model of misspecification which only requires the approximation error at each input $x$ to be proportional to the suboptimality gap at $x$. It captures the intuition that, for optimization problems, near-optimal regions should matter more and we can tolerate larger approximation errors in suboptimal regions. Quite surprisingly, we show that the classical LinUCB algorithm -- designed for the realizable case -- is automatically robust against such $\rho$-gap-adjusted misspecification with parameter $\rho$ diminishing at $O(1/(d \sqrt{\log T}))$. It achieves a near-optimal $O(\sqrt{T})$ regret for problems that the best-known regret is almost linear in time horizon $T$. We further advance this frontier by presenting a novel phased elimination-based algorithm whose gap-adjusted misspecification parameter $\rho = O(1/\sqrt{d})$ does not scale with $T$. This algorithm attains optimal $O(\sqrt{T})$ regret and is deployment-efficient, requiring only $\log T$ batches of exploration. It also enjoys an adaptive $O(\log T)$ regret when a constant suboptimality gap exists. Technically, our proof relies on a novel self-bounding argument that bounds the part of the regret due to misspecification by the regret itself, and a new inductive lemma that limits the misspecification error within the suboptimality gap for all valid actions in each batch selected by G-optimal design.

Counterfactual Samples Constructing and Training for Commonsense Statements Estimation

Plausibility Estimation (PE) plays a crucial role for enabling language models to objectively comprehend the real world. While large language models (LLMs) demonstrate remarkable capabilities in PE tasks but sometimes produce trivial commonsense errors due to the complexity of commonsense knowledge. They lack two key traits of an ideal PE model: a) Language-explainable: relying on critical word segments for decisions, and b) Commonsense-sensitive: detecting subtle linguistic variations in commonsense. To address these issues, we propose a novel model-agnostic method, referred to as Commonsense Counterfactual Samples Generating (CCSG). By training PE models with CCSG, we encourage them to focus on critical words, thereby enhancing both their language-explainable and commonsense-sensitive capabilities. Specifically, CCSG generates counterfactual samples by strategically replacing key words and introducing low-level dropout within sentences. These counterfactual samples are then incorporated into a sentence-level contrastive training framework to further enhance the model's learning process. Experimental results across nine diverse datasets demonstrate the effectiveness of CCSG in addressing commonsense reasoning challenges, with our CCSG method showing 3.07% improvement against the SOTA methods.

Constrained Multi-objective Bayesian Optimization through Optimistic Constraints Estimation

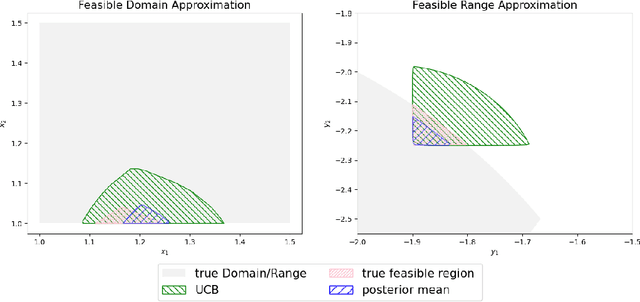
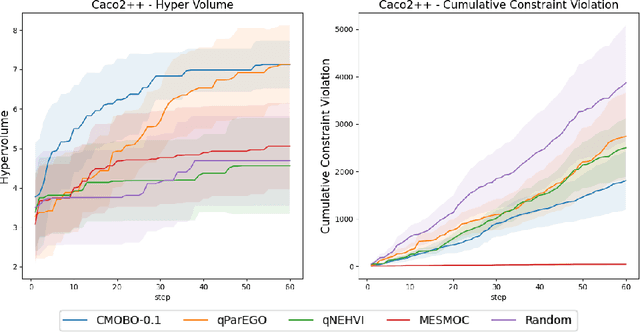
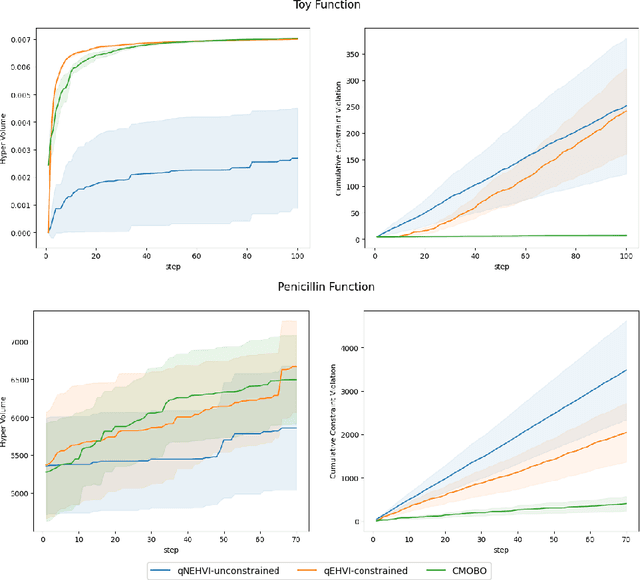
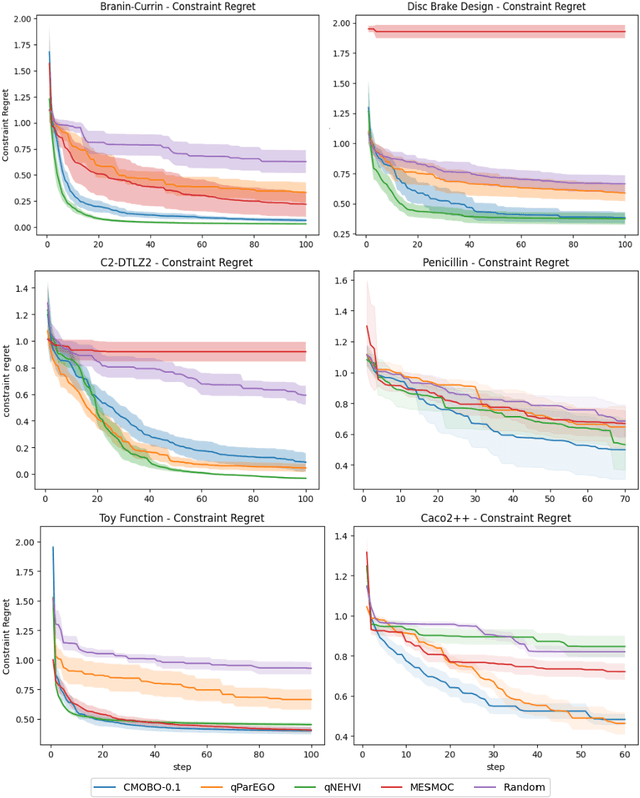
Multi-objective Bayesian optimization has been widely adopted in scientific experiment design, including drug discovery and hyperparameter optimization. In practice, regulatory or safety concerns often impose additional thresholds on certain attributes of the experimental outcomes. Previous work has primarily focused on constrained single-objective optimization tasks or active search under constraints. We propose CMOBO, a sample-efficient constrained multi-objective Bayesian optimization algorithm that balances learning of the feasible region (defined on multiple unknowns) with multi-objective optimization within the feasible region in a principled manner. We provide both theoretical justification and empirical evidence, demonstrating the efficacy of our approach on various synthetic benchmarks and real-world applications.

Improving Multi-modal Recommender Systems by Denoising and Aligning Multi-modal Content and User Feedback

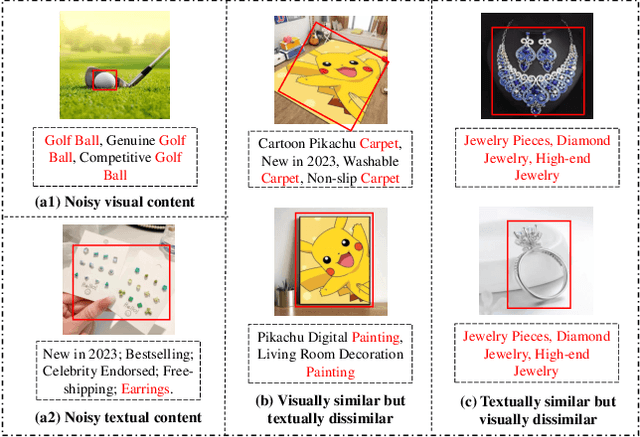
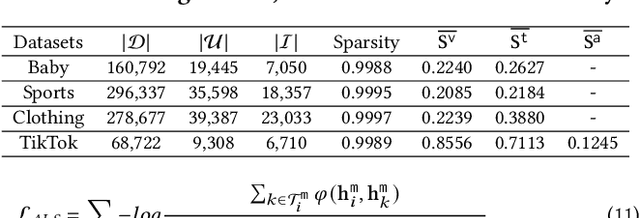
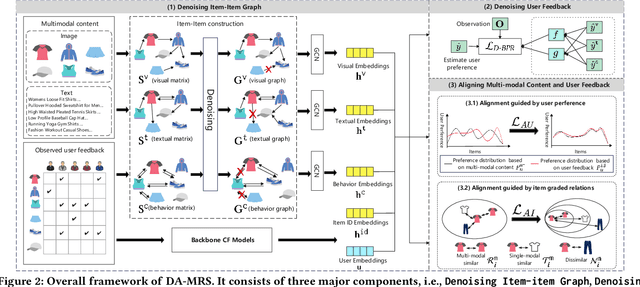
Multi-modal recommender systems (MRSs) are pivotal in diverse online web platforms and have garnered considerable attention in recent years. However, previous studies overlook the challenges of (1) noisy multi-modal content, (2) noisy user feedback, and (3) aligning multi-modal content with user feedback. In order to tackle these challenges, we propose Denoising and Aligning Multi-modal Recommender System (DA-MRS). To mitigate multi-modal noise, DA-MRS first constructs item-item graphs determined by consistent content similarity across modalities. To denoise user feedback, DA-MRS associates the probability of observed feedback with multi-modal content and devises a denoised BPR loss. Furthermore, DA-MRS implements Alignment guided by User preference to enhance task-specific item representation and Alignment guided by graded Item relations to provide finer-grained alignment. Extensive experiments verify that DA-MRS is a plug-and-play framework and achieves significant and consistent improvements across various datasets, backbone models, and noisy scenarios.