Sigma: Differential Rescaling of Query, Key and Value for Efficient Language Models

We introduce Sigma, an efficient large language model specialized for the system domain, empowered by a novel architecture including DiffQKV attention, and pre-trained on our meticulously collected system domain data. DiffQKV attention significantly enhances the inference efficiency of Sigma by optimizing the Query (Q), Key (K), and Value (V) components in the attention mechanism differentially, based on their varying impacts on the model performance and efficiency indicators. Specifically, we (1) conduct extensive experiments that demonstrate the model's varying sensitivity to the compression of K and V components, leading to the development of differentially compressed KV, and (2) propose augmented Q to expand the Q head dimension, which enhances the model's representation capacity with minimal impacts on the inference speed. Rigorous theoretical and empirical analyses reveal that DiffQKV attention significantly enhances efficiency, achieving up to a 33.36% improvement in inference speed over the conventional grouped-query attention (GQA) in long-context scenarios. We pre-train Sigma on 6T tokens from various sources, including 19.5B system domain data that we carefully collect and 1T tokens of synthesized and rewritten data. In general domains, Sigma achieves comparable performance to other state-of-arts models. In the system domain, we introduce the first comprehensive benchmark AIMicius, where Sigma demonstrates remarkable performance across all tasks, significantly outperforming GPT-4 with an absolute improvement up to 52.5%.

Using joint angles based on the international biomechanical standards for human action recognition and related tasks

Keypoint data has received a considerable amount of attention in machine learning for tasks like action detection and recognition. However, human experts in movement such as doctors, physiotherapists, sports scientists and coaches use a notion of joint angles standardised by the International Society of Biomechanics to precisely and efficiently communicate static body poses and movements. In this paper, we introduce the basic biomechanical notions and show how they can be used to convert common keypoint data into joint angles that uniquely describe the given pose and have various desirable mathematical properties, such as independence of both the camera viewpoint and the person performing the action. We experimentally demonstrate that the joint angle representation of keypoint data is suitable for machine learning applications and can in some cases bring an immediate performance gain. The use of joint angles as a human meaningful representation of kinematic data is in particular promising for applications where interpretability and dialog with human experts is important, such as many sports and medical applications. To facilitate further research in this direction, we will release a python package to convert keypoint data into joint angles as outlined in this paper.

MCGAN: Enhancing GAN Training with Regression-Based Generator Loss

Generative adversarial networks (GANs) have emerged as a powerful tool for generating high-fidelity data. However, the main bottleneck of existing approaches is the lack of supervision on the generator training, which often results in undamped oscillation and unsatisfactory performance. To address this issue, we propose an algorithm called Monte Carlo GAN (MCGAN). This approach, utilizing an innovative generative loss function, termly the regression loss, reformulates the generator training as a regression task and enables the generator training by minimizing the mean squared error between the discriminator's output of real data and the expected discriminator of fake data. We demonstrate the desirable analytic properties of the regression loss, including discriminability and optimality, and show that our method requires a weaker condition on the discriminator for effective generator training. These properties justify the strength of this approach to improve the training stability while retaining the optimality of GAN by leveraging strong supervision of the regression loss. Numerical results on CIFAR-10 and CIFAR-100 datasets demonstrate that the proposed MCGAN significantly and consistently improves the existing state-of-the-art GAN models in terms of quality, accuracy, training stability, and learned latent space. Furthermore, the proposed algorithm exhibits great flexibility for integrating with a variety of backbone models to generate spatial images, temporal time-series, and spatio-temporal video data.

High Rank Path Development: an approach of learning the filtration of stochastic processes

Since the weak convergence for stochastic processes does not account for the growth of information over time which is represented by the underlying filtration, a slightly erroneous stochastic model in weak topology may cause huge loss in multi-periods decision making problems. To address such discontinuities Aldous introduced the extended weak convergence, which can fully characterise all essential properties, including the filtration, of stochastic processes; however was considered to be hard to find efficient numerical implementations. In this paper, we introduce a novel metric called High Rank PCF Distance (HRPCFD) for extended weak convergence based on the high rank path development method from rough path theory, which also defines the characteristic function for measure-valued processes. We then show that such HRPCFD admits many favourable analytic properties which allows us to design an efficient algorithm for training HRPCFD from data and construct the HRPCF-GAN by using HRPCFD as the discriminator for conditional time series generation. Our numerical experiments on both hypothesis testing and generative modelling validate the out-performance of our approach compared with several state-of-the-art methods, highlighting its potential in broad applications of synthetic time series generation and in addressing classic financial and economic challenges, such as optimal stopping or utility maximisation problems.

GCN-DevLSTM: Path Development for Skeleton-Based Action Recognition

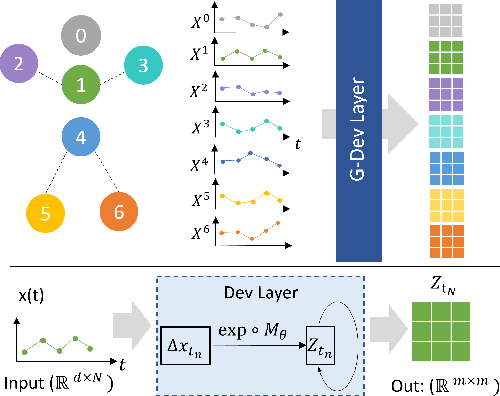
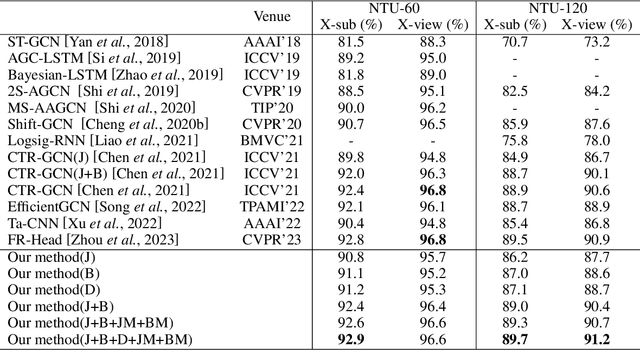
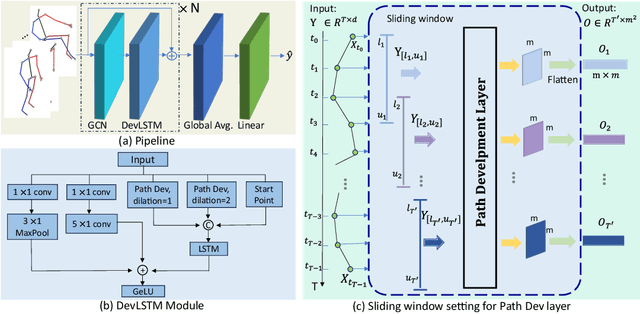
Skeleton-based action recognition (SAR) in videos is an important but challenging task in computer vision. The recent state-of-the-art models for SAR are primarily based on graph convolutional neural networks (GCNs), which are powerful in extracting the spatial information of skeleton data. However, it is yet clear that such GCN-based models can effectively capture the temporal dynamics of human action sequences. To this end, we propose the DevLSTM module, which exploits the path development -- a principled and parsimonious representation for sequential data by leveraging the Lie group structure. The path development, originated from Rough path theory, can effectively capture the order of events in high-dimensional stream data with massive dimension reduction and consequently enhance the LSTM module substantially. Our proposed G-DevLSTM module can be conveniently plugged into the temporal graph, complementing existing advanced GCN-based models. Our empirical studies on the NTU60, NTU120 and Chalearn2013 datasets demonstrate that our proposed hybrid model significantly outperforms the current best-performing methods in SAR tasks. The code is available at https://github.com/DeepIntoStreams/GCN-DevLSTM.

Part-Aware Transformer for Generalizable Person Re-identification

Domain generalization person re-identification (DG-ReID) aims to train a model on source domains and generalize well on unseen domains. Vision Transformer usually yields better generalization ability than common CNN networks under distribution shifts. However, Transformer-based ReID models inevitably over-fit to domain-specific biases due to the supervised learning strategy on the source domain. We observe that while the global images of different IDs should have different features, their similar local parts (e.g., black backpack) are not bounded by this constraint. Motivated by this, we propose a pure Transformer model (termed Part-aware Transformer) for DG-ReID by designing a proxy task, named Cross-ID Similarity Learning (CSL), to mine local visual information shared by different IDs. This proxy task allows the model to learn generic features because it only cares about the visual similarity of the parts regardless of the ID labels, thus alleviating the side effect of domain-specific biases. Based on the local similarity obtained in CSL, a Part-guided Self-Distillation (PSD) is proposed to further improve the generalization of global features. Our method achieves state-of-the-art performance under most DG ReID settings. Under the Market$\to$Duke setting, our method exceeds state-of-the-art by 10.9% and 12.8% in Rank1 and mAP, respectively. The code is available at https://github.com/liyuke65535/Part-Aware-Transformer.

Generative Modelling of Lévy Area for High Order SDE Simulation

It is well known that, when numerically simulating solutions to SDEs, achieving a strong convergence rate better than O(\sqrt{h}) (where h is the step size) requires the use of certain iterated integrals of Brownian motion, commonly referred to as its "L\'{e}vy areas". However, these stochastic integrals are difficult to simulate due to their non-Gaussian nature and for a d-dimensional Brownian motion with d > 2, no fast almost-exact sampling algorithm is known. In this paper, we propose L\'{e}vyGAN, a deep-learning-based model for generating approximate samples of L\'{e}vy area conditional on a Brownian increment. Due to our "Bridge-flipping" operation, the output samples match all joint and conditional odd moments exactly. Our generator employs a tailored GNN-inspired architecture, which enforces the correct dependency structure between the output distribution and the conditioning variable. Furthermore, we incorporate a mathematically principled characteristic-function based discriminator. Lastly, we introduce a novel training mechanism termed "Chen-training", which circumvents the need for expensive-to-generate training data-sets. This new training procedure is underpinned by our two main theoretical results. For 4-dimensional Brownian motion, we show that L\'{e}vyGAN exhibits state-of-the-art performance across several metrics which measure both the joint and marginal distributions. We conclude with a numerical experiment on the log-Heston model, a popular SDE in mathematical finance, demonstrating that high-quality synthetic L\'{e}vy area can lead to high order weak convergence and variance reduction when using multilevel Monte Carlo (MLMC).

Minimally-Supervised Speech Synthesis with Conditional Diffusion Model and Language Model: A Comparative Study of Semantic Coding

Recently, there has been a growing interest in text-to-speech (TTS) methods that can be trained with minimal supervision by combining two types of discrete speech representations and using two sequence-to-sequence tasks to decouple TTS. To address the challenges associated with high dimensionality and waveform distortion in discrete representations, we propose Diff-LM-Speech, which models semantic embeddings into mel-spectrogram based on diffusion models and introduces a prompt encoder structure based on variational autoencoders and prosody bottlenecks to improve prompt representation capabilities. Autoregressive language models often suffer from missing and repeated words, while non-autoregressive frameworks face expression averaging problems due to duration prediction models. To address these issues, we propose Tetra-Diff-Speech, which designs a duration diffusion model to achieve diverse prosodic expressions. While we expect the information content of semantic coding to be between that of text and acoustic coding, existing models extract semantic coding with a lot of redundant information and dimensionality explosion. To verify that semantic coding is not necessary, we propose Tri-Diff-Speech. Experimental results show that our proposed methods outperform baseline methods. We provide a website with audio samples.

A Neural RDE-based model for solving path-dependent PDEs

The concept of the path-dependent partial differential equation (PPDE) was first introduced in the context of path-dependent derivatives in financial markets. Its semilinear form was later identified as a non-Markovian backward stochastic differential equation (BSDE). Compared to the classical PDE, the solution of a PPDE involves an infinite-dimensional spatial variable, making it challenging to approximate, if not impossible. In this paper, we propose a neural rough differential equation (NRDE)-based model to learn PPDEs, which effectively encodes the path information through the log-signature feature while capturing the fundamental dynamics. The proposed continuous-time model for the PPDE solution offers the benefits of efficient memory usage and the ability to scale with dimensionality. Several numerical experiments, provided to validate the performance of the proposed model in comparison to the strong baseline in the literature, are used to demonstrate its effectiveness.

PCF-GAN: generating sequential data via the characteristic function of measures on the path space

Generating high-fidelity time series data using generative adversarial networks (GANs) remains a challenging task, as it is difficult to capture the temporal dependence of joint probability distributions induced by time-series data. Towards this goal, a key step is the development of an effective discriminator to distinguish between time series distributions. We propose the so-called PCF-GAN, a novel GAN that incorporates the path characteristic function (PCF) as the principled representation of time series distribution into the discriminator to enhance its generative performance. On the one hand, we establish theoretical foundations of the PCF distance by proving its characteristicity, boundedness, differentiability with respect to generator parameters, and weak continuity, which ensure the stability and feasibility of training the PCF-GAN. On the other hand, we design efficient initialisation and optimisation schemes for PCFs to strengthen the discriminative power and accelerate training efficiency. To further boost the capabilities of complex time series generation, we integrate the auto-encoder structure via sequential embedding into the PCF-GAN, which provides additional reconstruction functionality. Extensive numerical experiments on various datasets demonstrate the consistently superior performance of PCF-GAN over state-of-the-art baselines, in both generation and reconstruction quality. Code is available at https://github.com/DeepIntoStreams/PCF-GAN.