MCGAN: Enhancing GAN Training with Regression-Based Generator Loss
Paper and Code
May 27, 2024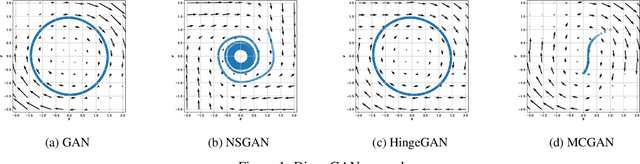

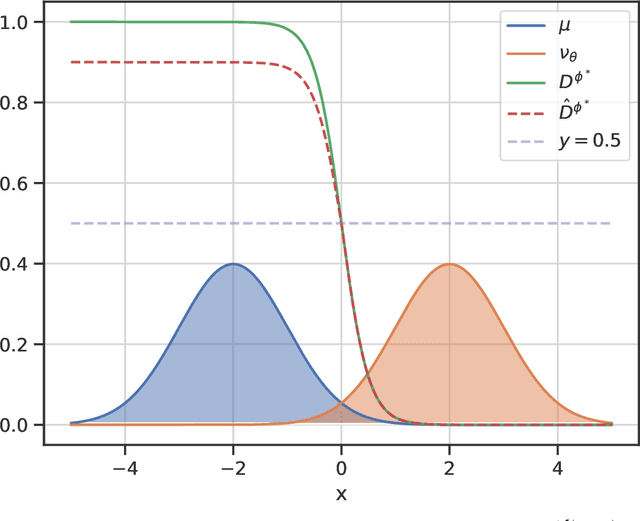
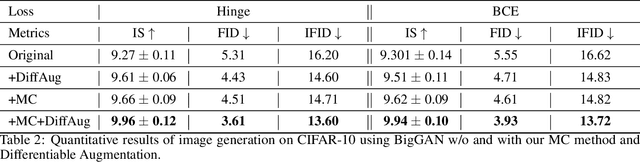
Generative adversarial networks (GANs) have emerged as a powerful tool for generating high-fidelity data. However, the main bottleneck of existing approaches is the lack of supervision on the generator training, which often results in undamped oscillation and unsatisfactory performance. To address this issue, we propose an algorithm called Monte Carlo GAN (MCGAN). This approach, utilizing an innovative generative loss function, termly the regression loss, reformulates the generator training as a regression task and enables the generator training by minimizing the mean squared error between the discriminator's output of real data and the expected discriminator of fake data. We demonstrate the desirable analytic properties of the regression loss, including discriminability and optimality, and show that our method requires a weaker condition on the discriminator for effective generator training. These properties justify the strength of this approach to improve the training stability while retaining the optimality of GAN by leveraging strong supervision of the regression loss. Numerical results on CIFAR-10 and CIFAR-100 datasets demonstrate that the proposed MCGAN significantly and consistently improves the existing state-of-the-art GAN models in terms of quality, accuracy, training stability, and learned latent space. Furthermore, the proposed algorithm exhibits great flexibility for integrating with a variety of backbone models to generate spatial images, temporal time-series, and spatio-temporal video data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge