MCGAN: Enhancing GAN Training with Regression-Based Generator Loss

Generative adversarial networks (GANs) have emerged as a powerful tool for generating high-fidelity data. However, the main bottleneck of existing approaches is the lack of supervision on the generator training, which often results in undamped oscillation and unsatisfactory performance. To address this issue, we propose an algorithm called Monte Carlo GAN (MCGAN). This approach, utilizing an innovative generative loss function, termly the regression loss, reformulates the generator training as a regression task and enables the generator training by minimizing the mean squared error between the discriminator's output of real data and the expected discriminator of fake data. We demonstrate the desirable analytic properties of the regression loss, including discriminability and optimality, and show that our method requires a weaker condition on the discriminator for effective generator training. These properties justify the strength of this approach to improve the training stability while retaining the optimality of GAN by leveraging strong supervision of the regression loss. Numerical results on CIFAR-10 and CIFAR-100 datasets demonstrate that the proposed MCGAN significantly and consistently improves the existing state-of-the-art GAN models in terms of quality, accuracy, training stability, and learned latent space. Furthermore, the proposed algorithm exhibits great flexibility for integrating with a variety of backbone models to generate spatial images, temporal time-series, and spatio-temporal video data.

Sig-Wasserstein GANs for Time Series Generation

Synthetic data is an emerging technology that can significantly accelerate the development and deployment of AI machine learning pipelines. In this work, we develop high-fidelity time-series generators, the SigWGAN, by combining continuous-time stochastic models with the newly proposed signature $W_1$ metric. The former are the Logsig-RNN models based on the stochastic differential equations, whereas the latter originates from the universal and principled mathematical features to characterize the measure induced by time series. SigWGAN allows turning computationally challenging GAN min-max problem into supervised learning while generating high fidelity samples. We validate the proposed model on both synthetic data generated by popular quantitative risk models and empirical financial data. Codes are available at https://github.com/SigCGANs/Sig-Wasserstein-GANs.git.

Conditional Sig-Wasserstein GANs for Time Series Generation

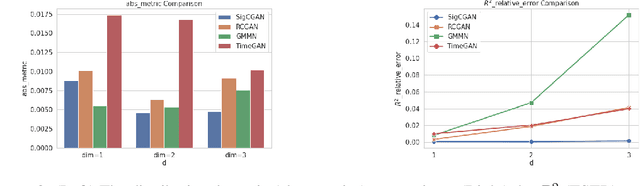
Generative adversarial networks (GANs) have been extremely successful in generating samples, from seemingly high dimensional probability measures. However, these methods struggle to capture the temporal dependence of joint probability distributions induced by time-series data. Furthermore, long time-series data streams hugely increase the dimension of the target space, which may render generative modeling infeasible. To overcome these challenges, we integrate GANs with mathematically principled and efficient path feature extraction called the signature of a path. The signature of a path is a graded sequence of statistics that provides a universal description for a stream of data, and its expected value characterizes the law of the time-series model. In particular, we a develop new metric, (conditional) Sig-$W_1$, that captures the (conditional) joint law of time series models, and use it as a discriminator. The signature feature space enables the explicit representation of the proposed discriminators which alleviates the need for expensive training. Furthermore, we develop a novel generator, called the conditional AR-FNN, which is designed to capture the temporal dependence of time series and can be efficiently trained. We validate our method on both synthetic and empirical datasets and observe that our method consistently and significantly outperforms state-of-the-art benchmarks with respect to measures of similarity and predictive ability.