Magnus Wiese
Sig-Splines: universal approximation and convex calibration of time series generative models
Jul 19, 2023



Abstract:We propose a novel generative model for multivariate discrete-time time series data. Drawing inspiration from the construction of neural spline flows, our algorithm incorporates linear transformations and the signature transform as a seamless substitution for traditional neural networks. This approach enables us to achieve not only the universality property inherent in neural networks but also introduces convexity in the model's parameters.
Deep Hedging: Continuous Reinforcement Learning for Hedging of General Portfolios across Multiple Risk Aversions
Jul 15, 2022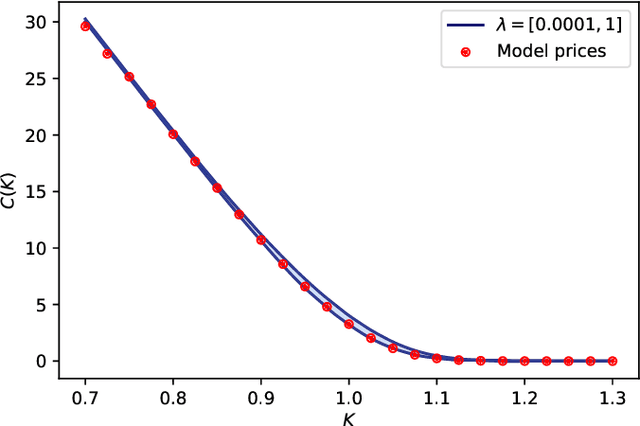

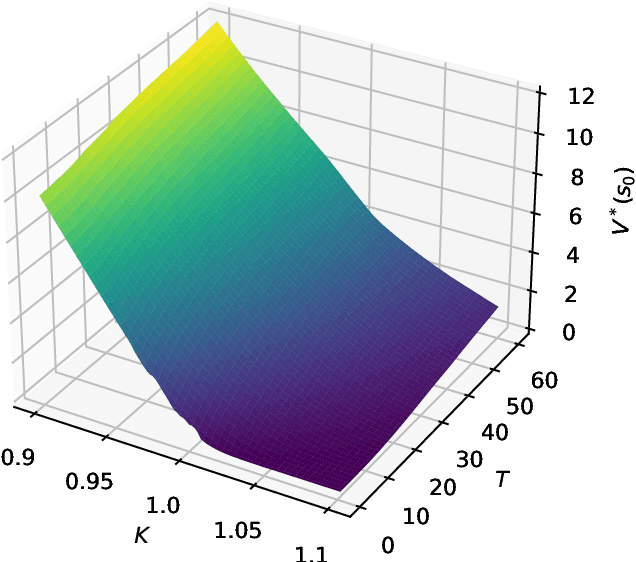
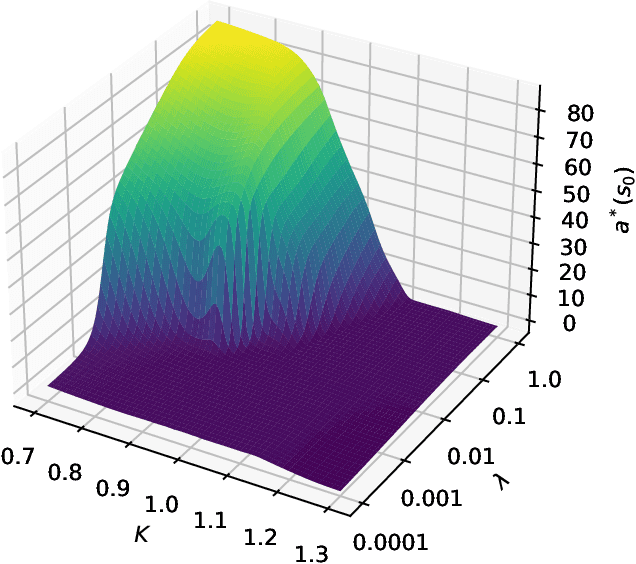
Abstract:We present a method for finding optimal hedging policies for arbitrary initial portfolios and market states. We develop a novel actor-critic algorithm for solving general risk-averse stochastic control problems and use it to learn hedging strategies across multiple risk aversion levels simultaneously. We demonstrate the effectiveness of the approach with a numerical example in a stochastic volatility environment.
Risk-Neutral Market Simulation
Feb 28, 2022
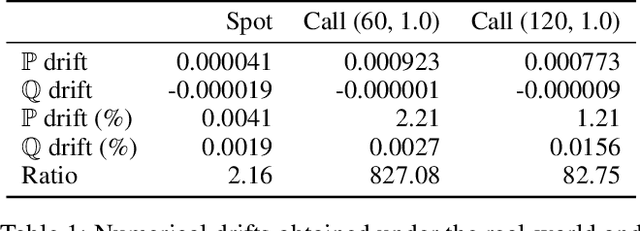


Abstract:We develop a risk-neutral spot and equity option market simulator for a single underlying, under which the joint market process is a martingale. We leverage an efficient low-dimensional representation of the market which preserves no static arbitrage, and employ neural spline flows to simulate samples which are free from conditional drifts and are highly realistic in the sense that among all possible risk-neutral simulators, the obtained risk-neutral simulator is the closest to the historical data with respect to the Kullback-Leibler divergence. Numerical experiments demonstrate the effectiveness and highlight both drift removal and fidelity of the calibrated simulator.
Multi-Asset Spot and Option Market Simulation
Dec 13, 2021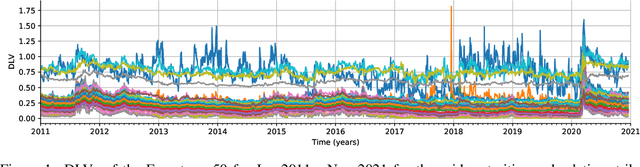

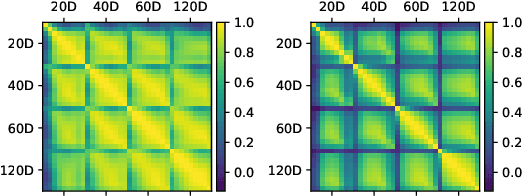

Abstract:We construct realistic spot and equity option market simulators for a single underlying on the basis of normalizing flows. We address the high-dimensionality of market observed call prices through an arbitrage-free autoencoder that approximates efficient low-dimensional representations of the prices while maintaining no static arbitrage in the reconstructed surface. Given a multi-asset universe, we leverage the conditional invertibility property of normalizing flows and introduce a scalable method to calibrate the joint distribution of a set of independent simulators while preserving the dynamics of each simulator. Empirical results highlight the goodness of the calibrated simulators and their fidelity.
Sig-Wasserstein GANs for Time Series Generation
Nov 01, 2021



Abstract:Synthetic data is an emerging technology that can significantly accelerate the development and deployment of AI machine learning pipelines. In this work, we develop high-fidelity time-series generators, the SigWGAN, by combining continuous-time stochastic models with the newly proposed signature $W_1$ metric. The former are the Logsig-RNN models based on the stochastic differential equations, whereas the latter originates from the universal and principled mathematical features to characterize the measure induced by time series. SigWGAN allows turning computationally challenging GAN min-max problem into supervised learning while generating high fidelity samples. We validate the proposed model on both synthetic data generated by popular quantitative risk models and empirical financial data. Codes are available at https://github.com/SigCGANs/Sig-Wasserstein-GANs.git.
Conditional Sig-Wasserstein GANs for Time Series Generation
Jun 09, 2020

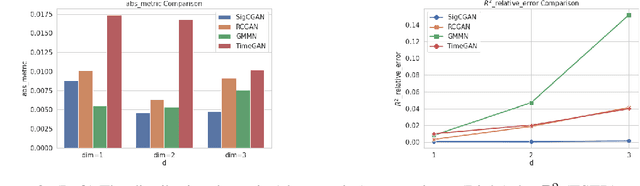

Abstract:Generative adversarial networks (GANs) have been extremely successful in generating samples, from seemingly high dimensional probability measures. However, these methods struggle to capture the temporal dependence of joint probability distributions induced by time-series data. Furthermore, long time-series data streams hugely increase the dimension of the target space, which may render generative modeling infeasible. To overcome these challenges, we integrate GANs with mathematically principled and efficient path feature extraction called the signature of a path. The signature of a path is a graded sequence of statistics that provides a universal description for a stream of data, and its expected value characterizes the law of the time-series model. In particular, we a develop new metric, (conditional) Sig-$W_1$, that captures the (conditional) joint law of time series models, and use it as a discriminator. The signature feature space enables the explicit representation of the proposed discriminators which alleviates the need for expensive training. Furthermore, we develop a novel generator, called the conditional AR-FNN, which is designed to capture the temporal dependence of time series and can be efficiently trained. We validate our method on both synthetic and empirical datasets and observe that our method consistently and significantly outperforms state-of-the-art benchmarks with respect to measures of similarity and predictive ability.
Deep Hedging: Learning to Simulate Equity Option Markets
Nov 05, 2019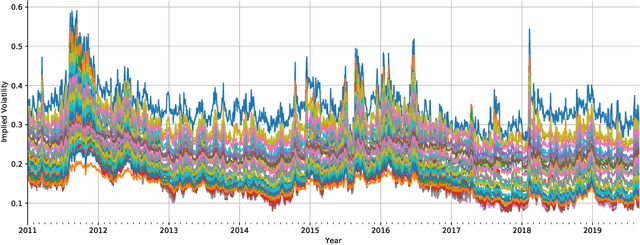

Abstract:We construct realistic equity option market simulators based on generative adversarial networks (GANs). We consider recurrent and temporal convolutional architectures, and assess the impact of state compression. Option market simulators are highly relevant because they allow us to extend the limited real-world data sets available for the training and evaluation of option trading strategies. We show that network-based generators outperform classical methods on a range of benchmark metrics, and adversarial training achieves the best performance. Our work demonstrates for the first time that GANs can be successfully applied to the task of generating multivariate financial time series.
Quant GANs: Deep Generation of Financial Time Series
Jul 15, 2019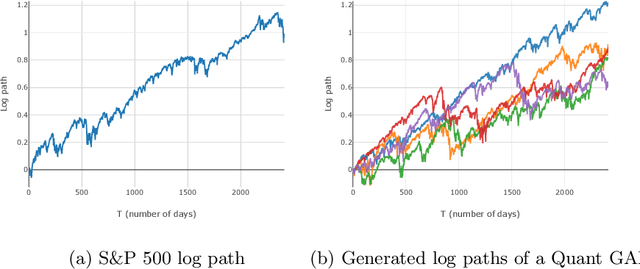

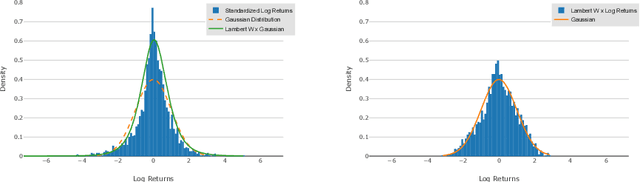
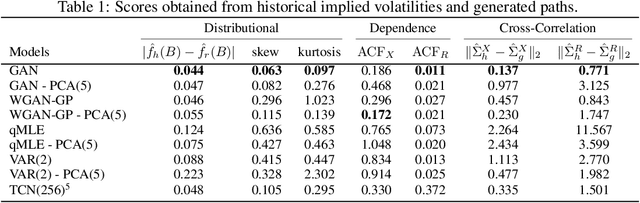
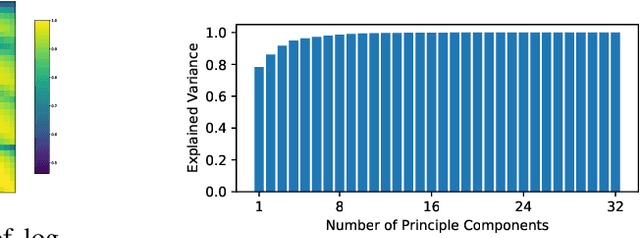
Abstract:Modeling financial time series by stochastic processes is a challenging task and a central area of research in financial mathematics. In this paper, we break through this barrier and present Quant GANs, a data-driven model which is inspired by the recent success of generative adversarial networks (GANs). Quant GANs consist of a generator and discriminator function which utilize temporal convolutional networks (TCNs) and thereby achieve to capture longer-ranging dependencies such as the presence of volatility clusters. Furthermore, the generator function is explicitly constructed such that the induced stochastic process allows a transition to its risk-neutral distribution. Our numerical results highlight that distributional properties for small and large lags are in an excellent agreement and dependence properties such as volatility clusters, leverage effects, and serial autocorrelations can be generated by the generator function of Quant GANs, demonstrably in high fidelity.
Copula & Marginal Flows: Disentangling the Marginal from its Joint
Jul 07, 2019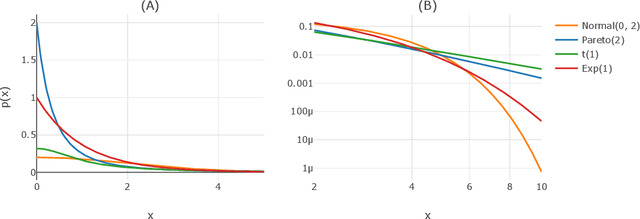

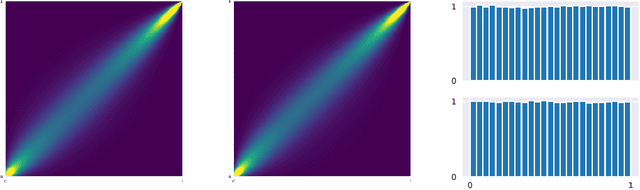
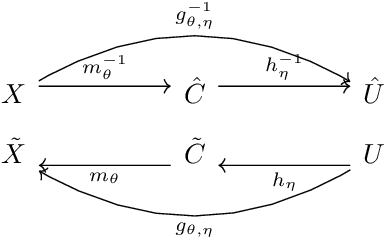
Abstract:Deep generative networks such as GANs and normalizing flows flourish in the context of high-dimensional tasks such as image generation. However, so far exact modeling or extrapolation of distributional properties such as the tail asymptotics generated by a generative network is not available. In this paper, we address this issue for the first time in the deep learning literature by making two novel contributions. First, we derive upper bounds for the tails that can be expressed by a generative network and demonstrate Lp-space related properties. There we show specifically that in various situations an optimal generative network does not exist. Second, we introduce and propose copula and marginal generative flows (CM flows) which allow for an exact modeling of the tail and any prior assumption on the CDF up to an approximation of the uniform distribution. Our numerical results support the use of CM flows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge