Fast Deep Hedging with Second-Order Optimization

Hedging exotic options in presence of market frictions is an important risk management task. Deep hedging can solve such hedging problems by training neural network policies in realistic simulated markets. Training these neural networks may be delicate and suffer from slow convergence, particularly for options with long maturities and complex sensitivities to market parameters. To address this, we propose a second-order optimization scheme for deep hedging. We leverage pathwise differentiability to construct a curvature matrix, which we approximate as block-diagonal and Kronecker-factored to efficiently precondition gradients. We evaluate our method on a challenging and practically important problem: hedging a cliquet option on a stock with stochastic volatility by trading in the spot and vanilla options. We find that our second-order scheme can optimize the policy in 1/4 of the number of steps that standard adaptive moment-based optimization takes.

Quantum Deep Hedging

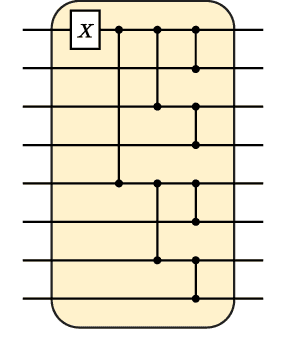
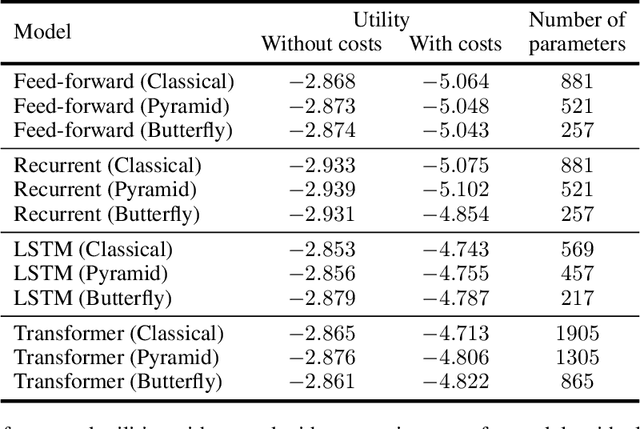
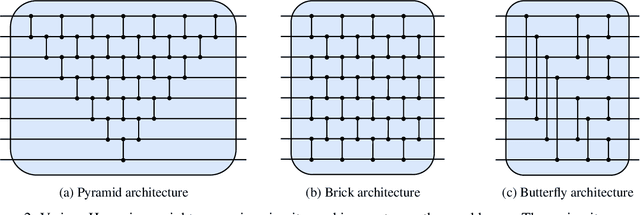
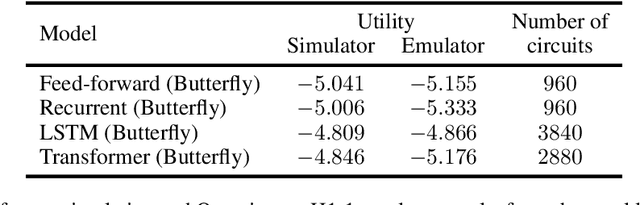
Quantum machine learning has the potential for a transformative impact across industry sectors and in particular in finance. In our work we look at the problem of hedging where deep reinforcement learning offers a powerful framework for real markets. We develop quantum reinforcement learning methods based on policy-search and distributional actor-critic algorithms that use quantum neural network architectures with orthogonal and compound layers for the policy and value functions. We prove that the quantum neural networks we use are trainable, and we perform extensive simulations that show that quantum models can reduce the number of trainable parameters while achieving comparable performance and that the distributional approach obtains better performance than other standard approaches, both classical and quantum. We successfully implement the proposed models on a trapped-ion quantum processor, utilizing circuits with up to $16$ qubits, and observe performance that agrees well with noiseless simulation. Our quantum techniques are general and can be applied to other reinforcement learning problems beyond hedging.

Deep Hedging: Continuous Reinforcement Learning for Hedging of General Portfolios across Multiple Risk Aversions

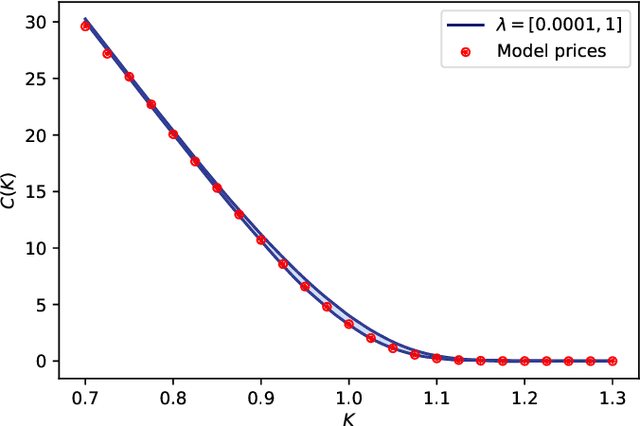
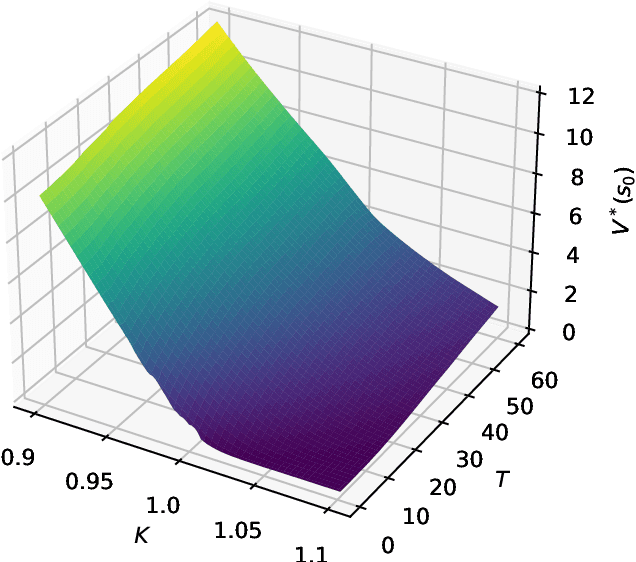
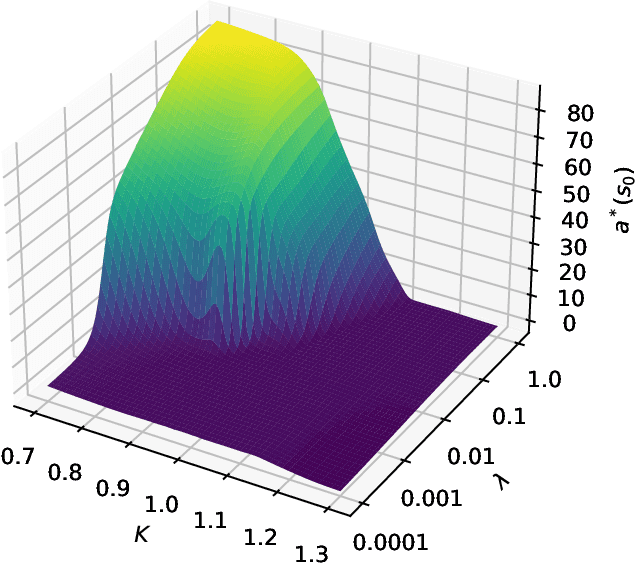
We present a method for finding optimal hedging policies for arbitrary initial portfolios and market states. We develop a novel actor-critic algorithm for solving general risk-averse stochastic control problems and use it to learn hedging strategies across multiple risk aversion levels simultaneously. We demonstrate the effectiveness of the approach with a numerical example in a stochastic volatility environment.

Multi-Asset Spot and Option Market Simulation

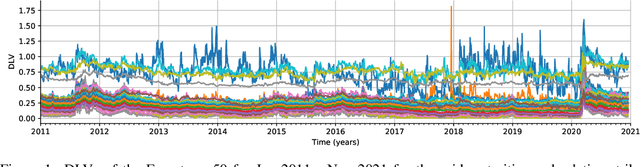
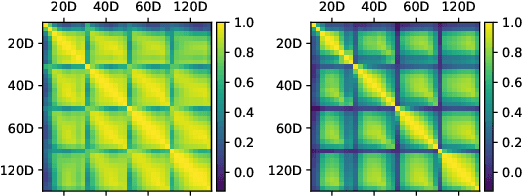
We construct realistic spot and equity option market simulators for a single underlying on the basis of normalizing flows. We address the high-dimensionality of market observed call prices through an arbitrage-free autoencoder that approximates efficient low-dimensional representations of the prices while maintaining no static arbitrage in the reconstructed surface. Given a multi-asset universe, we leverage the conditional invertibility property of normalizing flows and introduce a scalable method to calibrate the joint distribution of a set of independent simulators while preserving the dynamics of each simulator. Empirical results highlight the goodness of the calibrated simulators and their fidelity.

Deep Hedging: Learning to Remove the Drift under Trading Frictions with Minimal Equivalent Near-Martingale Measures

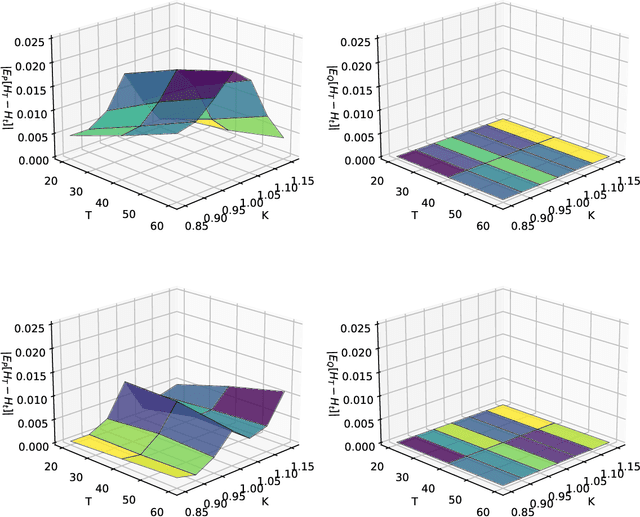
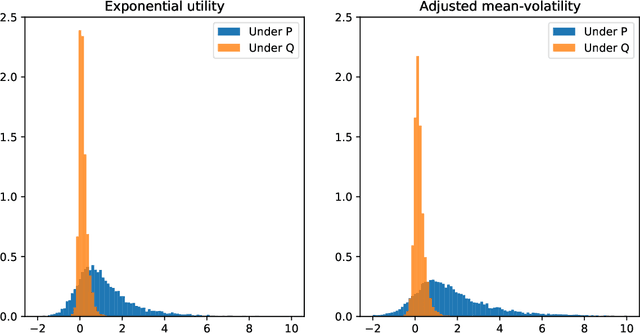
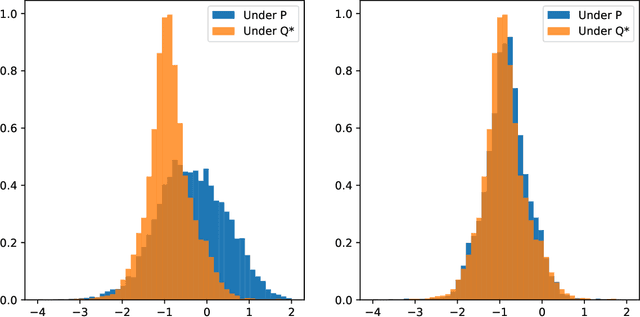
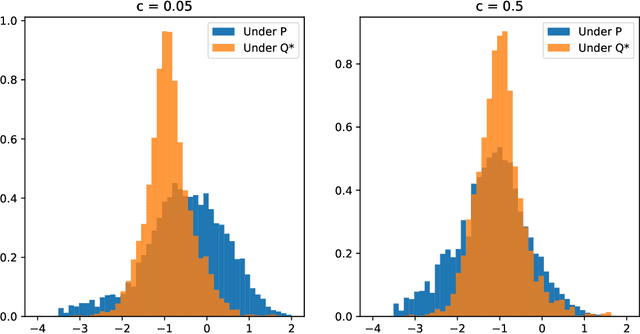
We present a numerically efficient approach for learning minimal equivalent martingale measures for market simulators of tradable instruments, e.g. for a spot price and options written on the same underlying. In the presence of transaction cost and trading restrictions, we relax the results to learning minimal equivalent "near-martingale measures" under which expected returns remain within prevailing bid/ask spreads. Our approach to thus "removing the drift" in a high dimensional complex space is entirely model-free and can be applied to any market simulator which does not exhibit classic arbitrage. The resulting model can be used for risk neutral pricing, or, in the case of transaction costs or trading constraints, for "Deep Hedging". We demonstrate our approach by applying it to two market simulators, an auto-regressive discrete-time stochastic implied volatility model, and a Generative Adversarial Network (GAN) based simulator, both of which trained on historical data of option prices under the statistical measure to produce realistic samples of spot and option prices. We comment on robustness with respect to estimation error of the original market simulator.

Deep Hedging: Learning Risk-Neutral Implied Volatility Dynamics

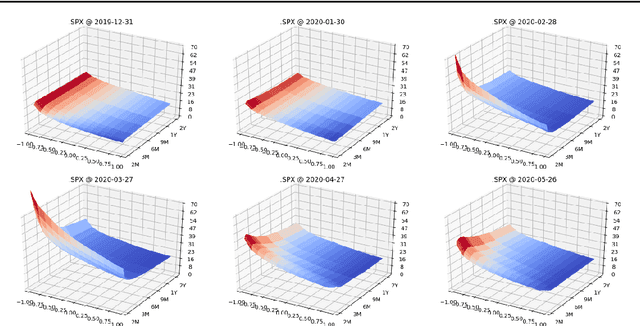
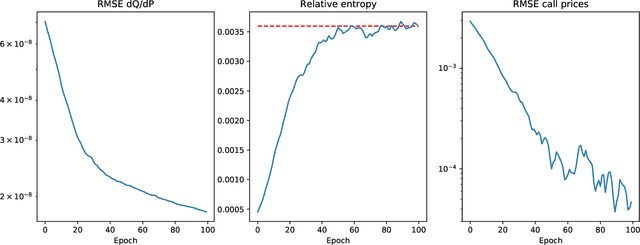
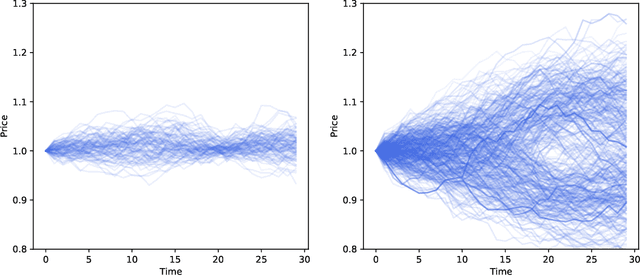
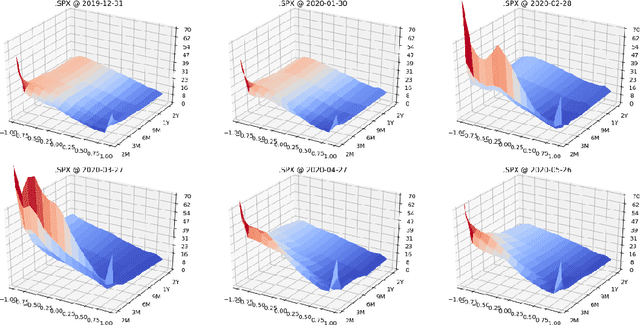
We present a numerically efficient approach for learning a risk-neutral measure for paths of simulated spot and option prices up to a finite horizon under convex transaction costs and convex trading constraints. This approach can then be used to implement a stochastic implied volatility model in the following two steps: 1. Train a market simulator for option prices, as discussed for example in our recent; 2. Find a risk-neutral density, specifically the minimal entropy martingale measure. The resulting model can be used for risk-neutral pricing, or for Deep Hedging in the case of transaction costs or trading constraints. To motivate the proposed approach, we also show that market dynamics are free from "statistical arbitrage" in the absence of transaction costs if and only if they follow a risk-neutral measure. We additionally provide a more general characterization in the presence of convex transaction costs and trading constraints. These results can be seen as an analogue of the fundamental theorem of asset pricing for statistical arbitrage under trading frictions and are of independent interest.

A Data-driven Market Simulator for Small Data Environments

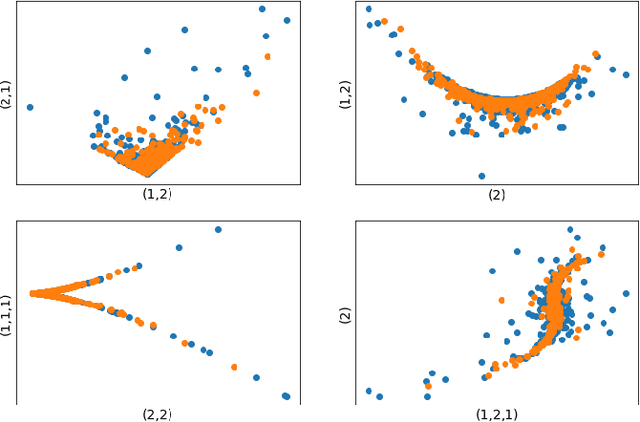
Neural network based data-driven market simulation unveils a new and flexible way of modelling financial time series without imposing assumptions on the underlying stochastic dynamics. Though in this sense generative market simulation is model-free, the concrete modelling choices are nevertheless decisive for the features of the simulated paths. We give a brief overview of currently used generative modelling approaches and performance evaluation metrics for financial time series, and address some of the challenges to achieve good results in the latter. We also contrast some classical approaches of market simulation with simulation based on generative modelling and highlight some advantages and pitfalls of the new approach. While most generative models tend to rely on large amounts of training data, we present here a generative model that works reliably in environments where the amount of available training data is notoriously small. Furthermore, we show how a rough paths perspective combined with a parsimonious Variational Autoencoder framework provides a powerful way for encoding and evaluating financial time series in such environments where available training data is scarce. Finally, we also propose a suitable performance evaluation metric for financial time series and discuss some connections of our Market Generator to deep hedging.

Deep Hedging: Learning to Simulate Equity Option Markets

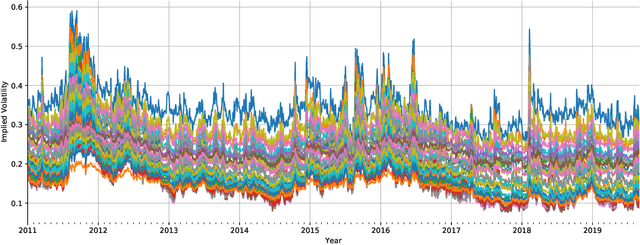
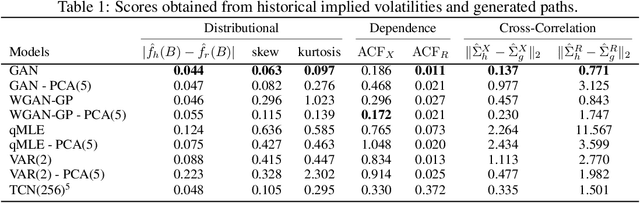
We construct realistic equity option market simulators based on generative adversarial networks (GANs). We consider recurrent and temporal convolutional architectures, and assess the impact of state compression. Option market simulators are highly relevant because they allow us to extend the limited real-world data sets available for the training and evaluation of option trading strategies. We show that network-based generators outperform classical methods on a range of benchmark metrics, and adversarial training achieves the best performance. Our work demonstrates for the first time that GANs can be successfully applied to the task of generating multivariate financial time series.