Sig-Splines: universal approximation and convex calibration of time series generative models

We propose a novel generative model for multivariate discrete-time time series data. Drawing inspiration from the construction of neural spline flows, our algorithm incorporates linear transformations and the signature transform as a seamless substitution for traditional neural networks. This approach enables us to achieve not only the universality property inherent in neural networks but also introduces convexity in the model's parameters.

Deep Hedging: Continuous Reinforcement Learning for Hedging of General Portfolios across Multiple Risk Aversions

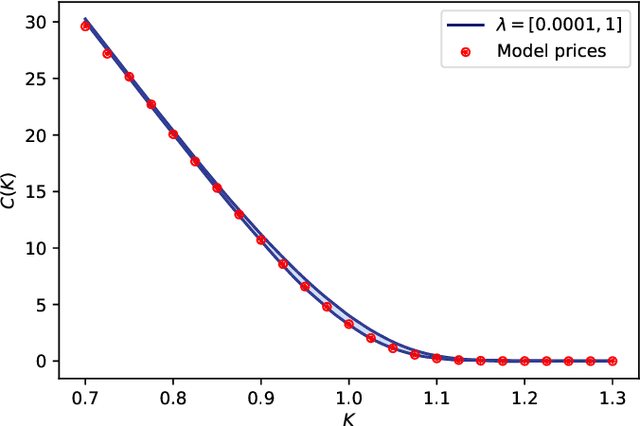
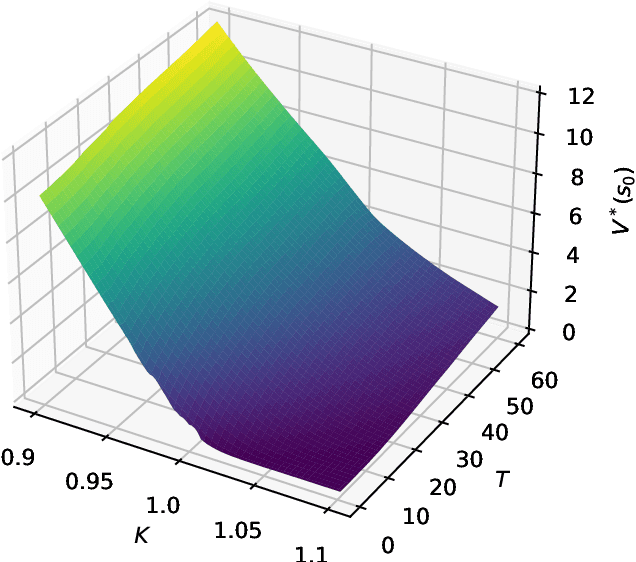
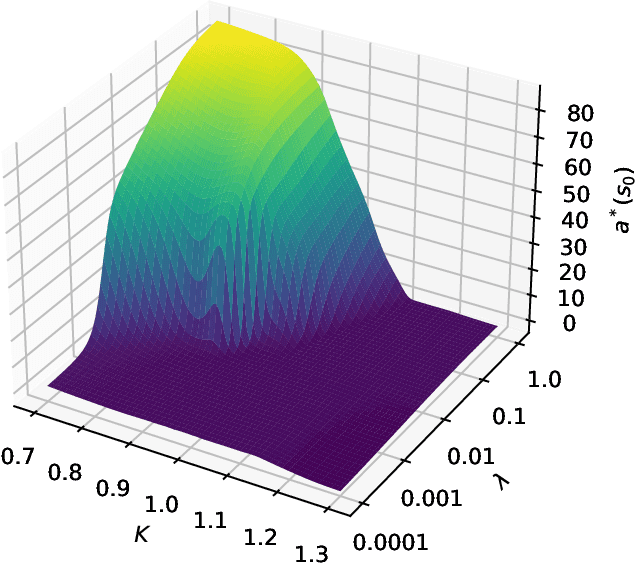
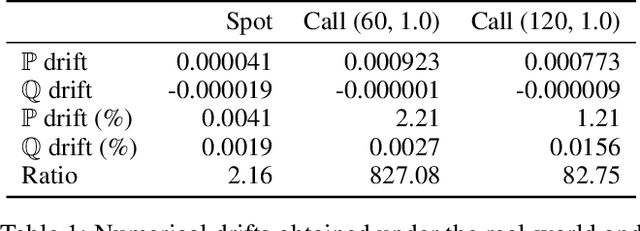
We present a method for finding optimal hedging policies for arbitrary initial portfolios and market states. We develop a novel actor-critic algorithm for solving general risk-averse stochastic control problems and use it to learn hedging strategies across multiple risk aversion levels simultaneously. We demonstrate the effectiveness of the approach with a numerical example in a stochastic volatility environment.

Risk-Neutral Market Simulation

We develop a risk-neutral spot and equity option market simulator for a single underlying, under which the joint market process is a martingale. We leverage an efficient low-dimensional representation of the market which preserves no static arbitrage, and employ neural spline flows to simulate samples which are free from conditional drifts and are highly realistic in the sense that among all possible risk-neutral simulators, the obtained risk-neutral simulator is the closest to the historical data with respect to the Kullback-Leibler divergence. Numerical experiments demonstrate the effectiveness and highlight both drift removal and fidelity of the calibrated simulator.

Multi-Asset Spot and Option Market Simulation

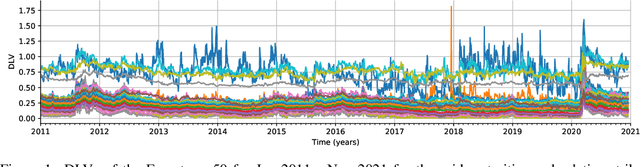
We construct realistic spot and equity option market simulators for a single underlying on the basis of normalizing flows. We address the high-dimensionality of market observed call prices through an arbitrage-free autoencoder that approximates efficient low-dimensional representations of the prices while maintaining no static arbitrage in the reconstructed surface. Given a multi-asset universe, we leverage the conditional invertibility property of normalizing flows and introduce a scalable method to calibrate the joint distribution of a set of independent simulators while preserving the dynamics of each simulator. Empirical results highlight the goodness of the calibrated simulators and their fidelity.

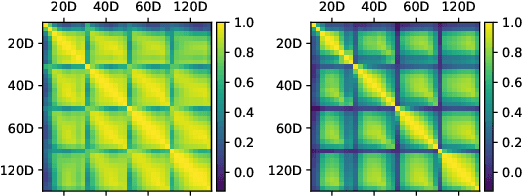
Deep Hedging: Learning to Remove the Drift under Trading Frictions with Minimal Equivalent Near-Martingale Measures

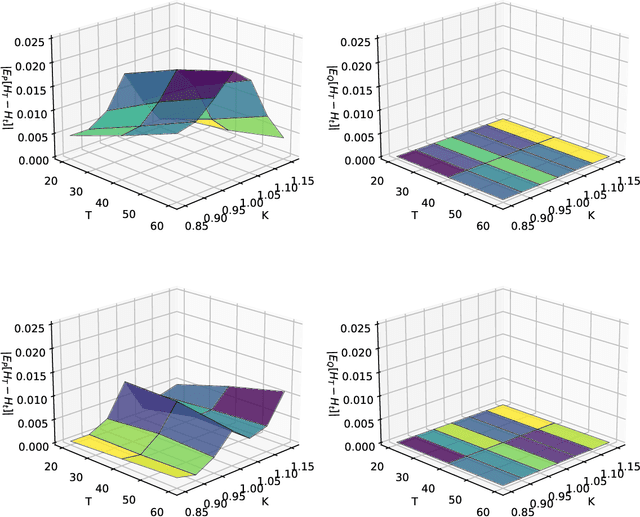
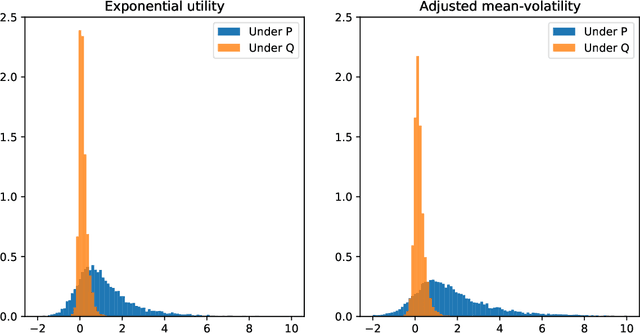
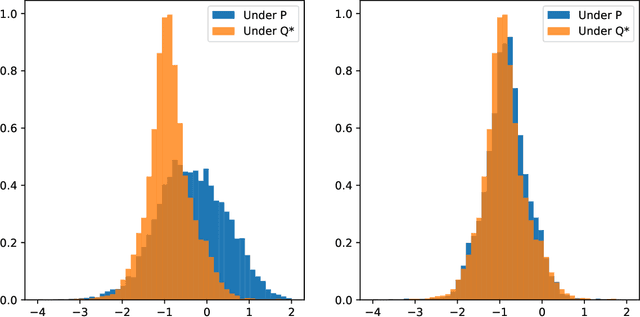
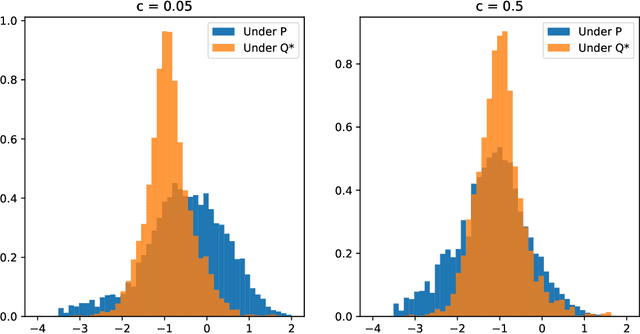
We present a numerically efficient approach for learning minimal equivalent martingale measures for market simulators of tradable instruments, e.g. for a spot price and options written on the same underlying. In the presence of transaction cost and trading restrictions, we relax the results to learning minimal equivalent "near-martingale measures" under which expected returns remain within prevailing bid/ask spreads. Our approach to thus "removing the drift" in a high dimensional complex space is entirely model-free and can be applied to any market simulator which does not exhibit classic arbitrage. The resulting model can be used for risk neutral pricing, or, in the case of transaction costs or trading constraints, for "Deep Hedging". We demonstrate our approach by applying it to two market simulators, an auto-regressive discrete-time stochastic implied volatility model, and a Generative Adversarial Network (GAN) based simulator, both of which trained on historical data of option prices under the statistical measure to produce realistic samples of spot and option prices. We comment on robustness with respect to estimation error of the original market simulator.

Deep Hedging: Learning Risk-Neutral Implied Volatility Dynamics

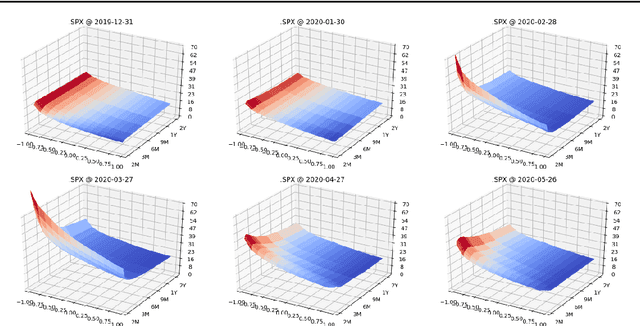
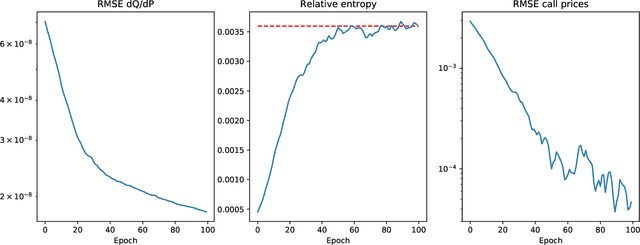
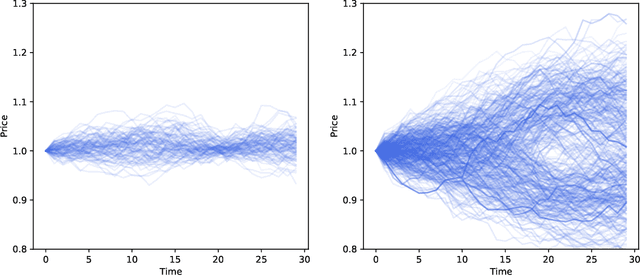
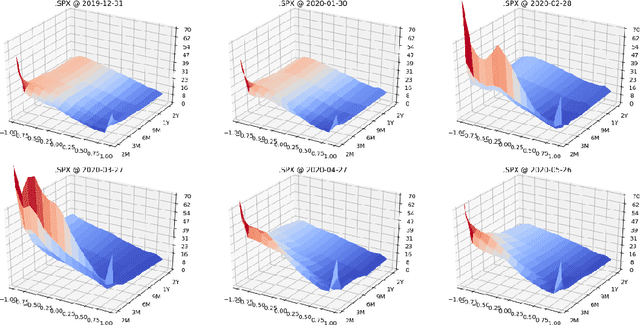
We present a numerically efficient approach for learning a risk-neutral measure for paths of simulated spot and option prices up to a finite horizon under convex transaction costs and convex trading constraints. This approach can then be used to implement a stochastic implied volatility model in the following two steps: 1. Train a market simulator for option prices, as discussed for example in our recent; 2. Find a risk-neutral density, specifically the minimal entropy martingale measure. The resulting model can be used for risk-neutral pricing, or for Deep Hedging in the case of transaction costs or trading constraints. To motivate the proposed approach, we also show that market dynamics are free from "statistical arbitrage" in the absence of transaction costs if and only if they follow a risk-neutral measure. We additionally provide a more general characterization in the presence of convex transaction costs and trading constraints. These results can be seen as an analogue of the fundamental theorem of asset pricing for statistical arbitrage under trading frictions and are of independent interest.