Ralf Korn
Sig-Splines: universal approximation and convex calibration of time series generative models
Jul 19, 2023Abstract:We propose a novel generative model for multivariate discrete-time time series data. Drawing inspiration from the construction of neural spline flows, our algorithm incorporates linear transformations and the signature transform as a seamless substitution for traditional neural networks. This approach enables us to achieve not only the universality property inherent in neural networks but also introduces convexity in the model's parameters.
Multi-Asset Spot and Option Market Simulation
Dec 13, 2021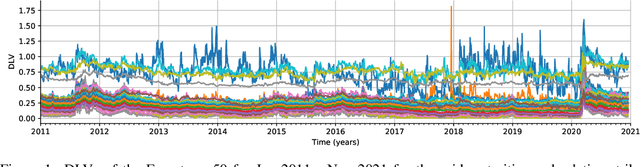


Abstract:We construct realistic spot and equity option market simulators for a single underlying on the basis of normalizing flows. We address the high-dimensionality of market observed call prices through an arbitrage-free autoencoder that approximates efficient low-dimensional representations of the prices while maintaining no static arbitrage in the reconstructed surface. Given a multi-asset universe, we leverage the conditional invertibility property of normalizing flows and introduce a scalable method to calibrate the joint distribution of a set of independent simulators while preserving the dynamics of each simulator. Empirical results highlight the goodness of the calibrated simulators and their fidelity.
Estimating the Value-at-Risk by Temporal VAE
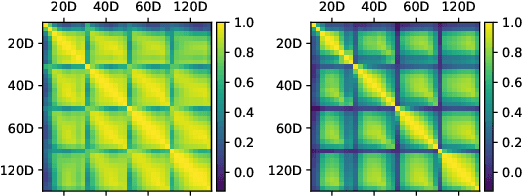
Dec 03, 2021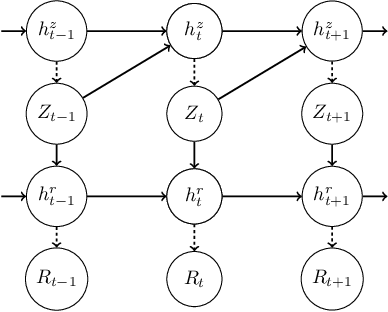
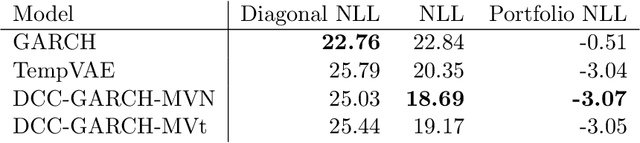
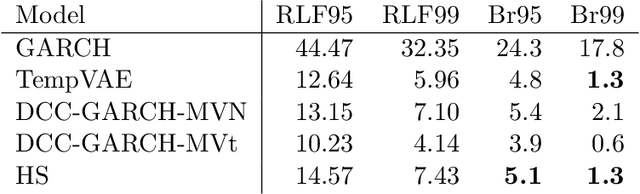
Abstract:Estimation of the value-at-risk (VaR) of a large portfolio of assets is an important task for financial institutions. As the joint log-returns of asset prices can often be projected to a latent space of a much smaller dimension, the use of a variational autoencoder (VAE) for estimating the VaR is a natural suggestion. To ensure the bottleneck structure of autoencoders when learning sequential data, we use a temporal VAE (TempVAE) that avoids an auto-regressive structure for the observation variables. However, the low signal- to-noise ratio of financial data in combination with the auto-pruning property of a VAE typically makes the use of a VAE prone to posterior collapse. Therefore, we propose to use annealing of the regularization to mitigate this effect. As a result, the auto-pruning of the TempVAE works properly which also results in excellent estimation results for the VaR that beats classical GARCH-type and historical simulation approaches when applied to real data.
A Generalised Linear Model Framework for Variational Autoencoders based on Exponential Dispersion Families
Jun 11, 2020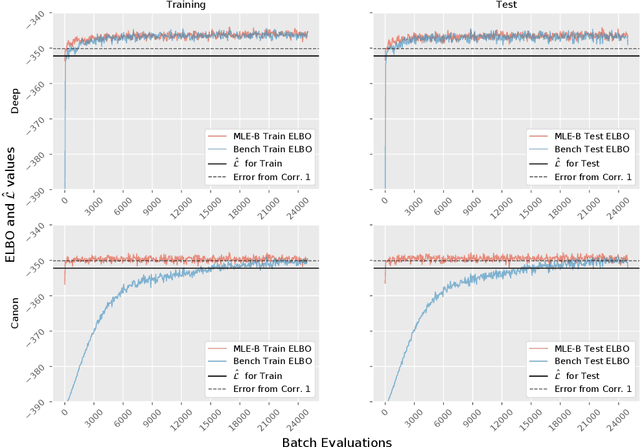


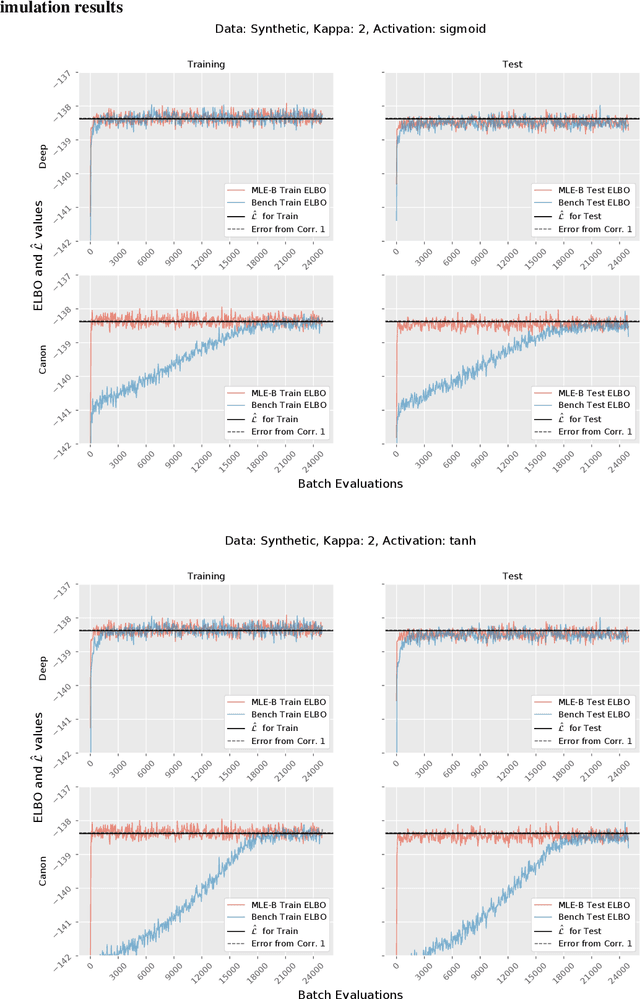
Abstract:Although variational autoencoders (VAE) are successfully used to obtain meaningful low-dimensional representations for high-dimensional data, aspects of their loss function are not yet fully understood. We introduce a theoretical framework that is based on a connection between VAE and generalized linear models (GLM). The equality between the activation function of a VAE and the inverse of the link function of a GLM enables us to provide a systematic generalization of the loss analysis for VAE based on the assumption that the distribution of the decoder belongs to an exponential dispersion family (EDF). As a further result, we can initialize VAE nets by maximum likelihood estimates (MLE) that enhance the training performance on both synthetic and real world data sets.
A lower bound for the ELBO of the Bernoulli Variational Autoencoder
Mar 26, 2020
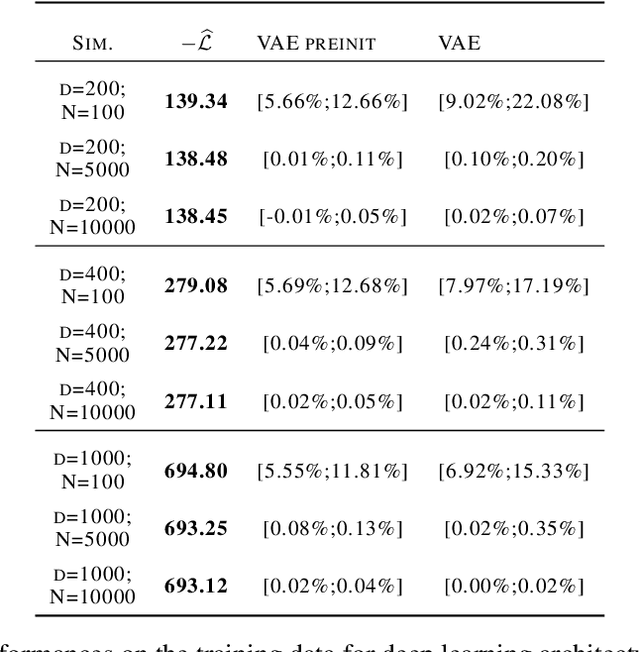
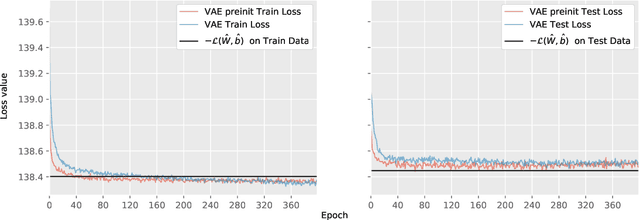
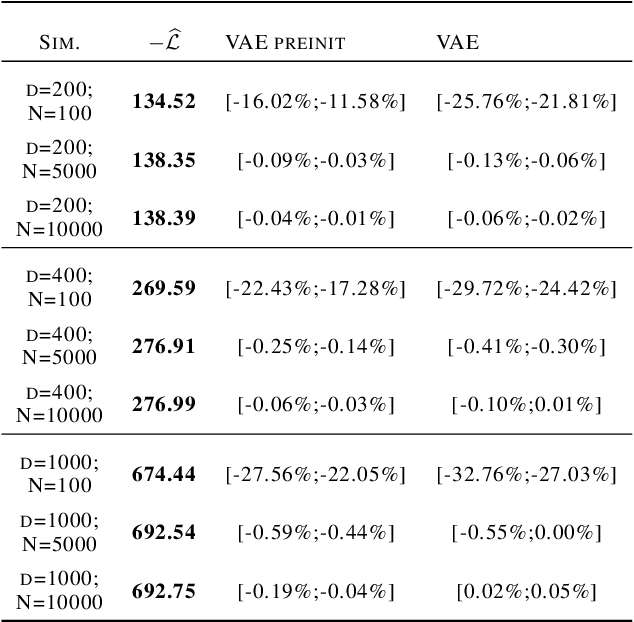
Abstract:We consider a variational autoencoder (VAE) for binary data. Our main innovations are an interpretable lower bound for its training objective, a modified initialization and architecture of such a VAE that leads to faster training, and a decision support for finding the appropriate dimension of the latent space via using a PCA. Numerical examples illustrate our theoretical result and the performance of the new architecture.
Machine Learning in Least-Squares Monte Carlo Proxy Modeling of Life Insurance Companies
Sep 05, 2019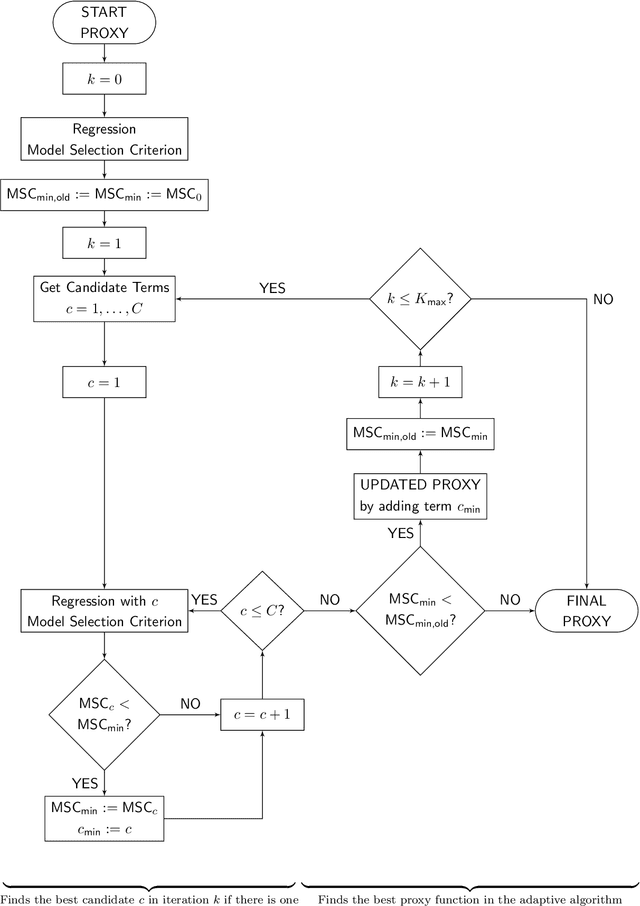
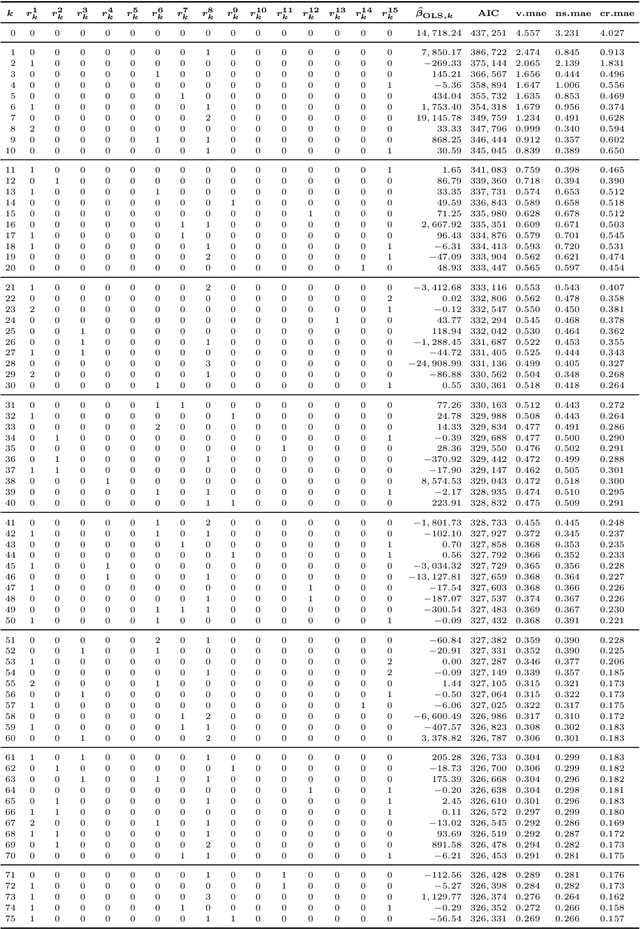
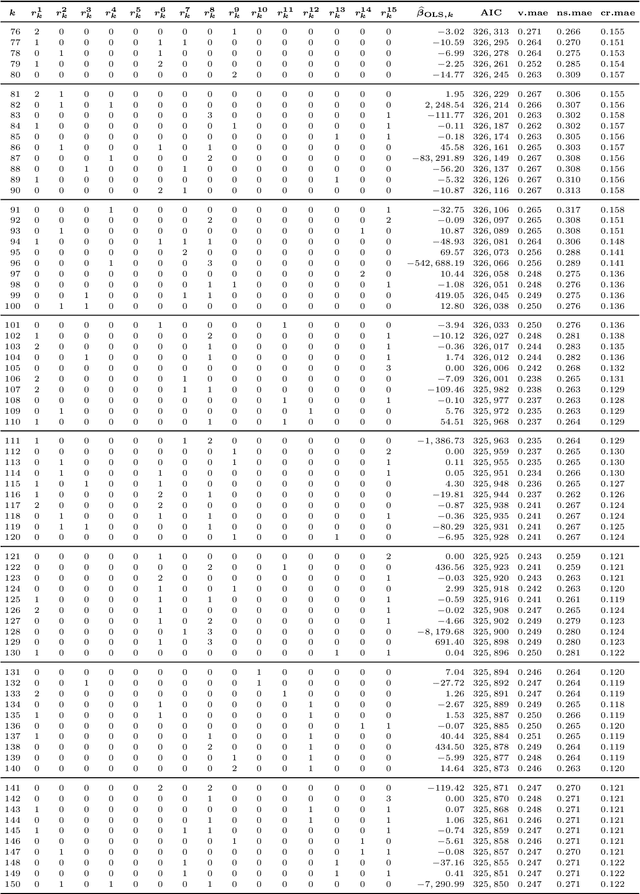
Abstract:Under the Solvency II regime, life insurance companies are asked to derive their solvency capital requirements from the full loss distributions over the coming year. Since the industry is currently far from being endowed with sufficient computational capacities to fully simulate these distributions, the insurers have to rely on suitable approximation techniques such as the least-squares Monte Carlo (LSMC) method. The key idea of LSMC is to run only a few wisely selected simulations and to process their output further to obtain a risk-dependent proxy function of the loss. In this paper, we present and analyze various adaptive machine learning approaches that can take over the proxy modeling task. The studied approaches range from ordinary and generalized least-squares regression variants over GLM and GAM methods to MARS and kernel regression routines. We justify the combinability of their regression ingredients in a theoretical discourse. Further, we illustrate the approaches in slightly disguised real-world experiments and perform comprehensive out-of-sample tests.
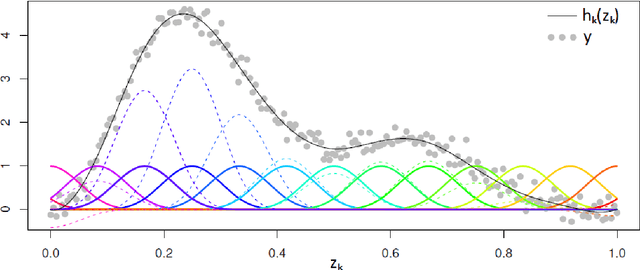
Quant GANs: Deep Generation of Financial Time Series
Jul 15, 2019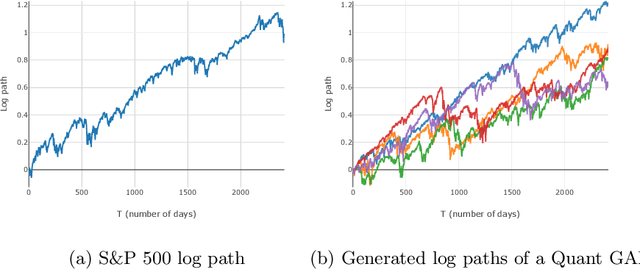

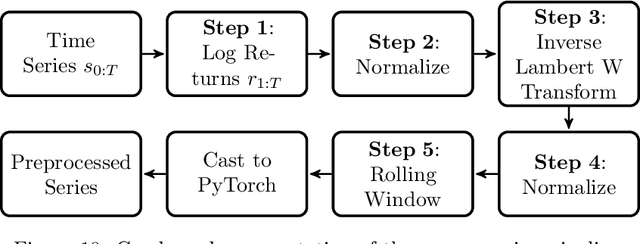
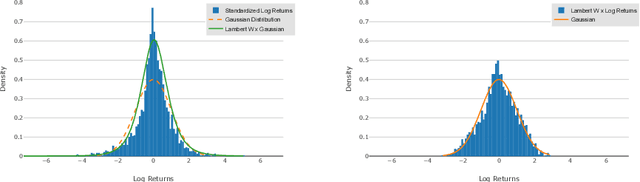
Abstract:Modeling financial time series by stochastic processes is a challenging task and a central area of research in financial mathematics. In this paper, we break through this barrier and present Quant GANs, a data-driven model which is inspired by the recent success of generative adversarial networks (GANs). Quant GANs consist of a generator and discriminator function which utilize temporal convolutional networks (TCNs) and thereby achieve to capture longer-ranging dependencies such as the presence of volatility clusters. Furthermore, the generator function is explicitly constructed such that the induced stochastic process allows a transition to its risk-neutral distribution. Our numerical results highlight that distributional properties for small and large lags are in an excellent agreement and dependence properties such as volatility clusters, leverage effects, and serial autocorrelations can be generated by the generator function of Quant GANs, demonstrably in high fidelity.
Copula & Marginal Flows: Disentangling the Marginal from its Joint
Jul 07, 2019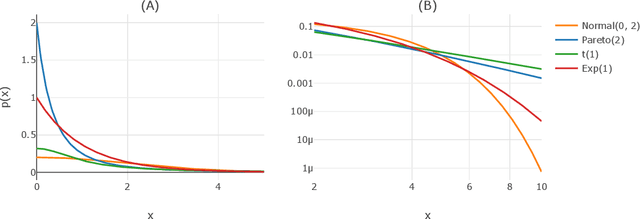

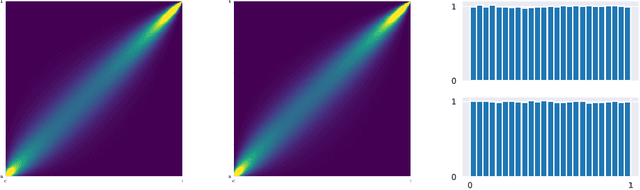
Abstract:Deep generative networks such as GANs and normalizing flows flourish in the context of high-dimensional tasks such as image generation. However, so far exact modeling or extrapolation of distributional properties such as the tail asymptotics generated by a generative network is not available. In this paper, we address this issue for the first time in the deep learning literature by making two novel contributions. First, we derive upper bounds for the tails that can be expressed by a generative network and demonstrate Lp-space related properties. There we show specifically that in various situations an optimal generative network does not exist. Second, we introduce and propose copula and marginal generative flows (CM flows) which allow for an exact modeling of the tail and any prior assumption on the CDF up to an approximation of the uniform distribution. Our numerical results support the use of CM flows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge