Quant GANs: Deep Generation of Financial Time Series
Paper and Code
Jul 15, 2019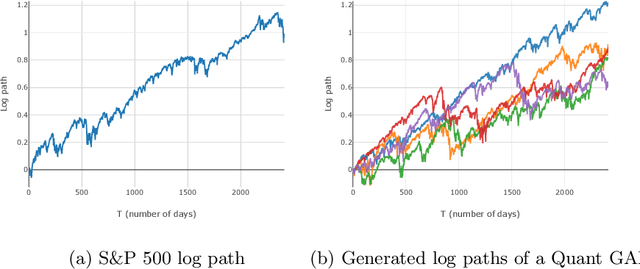

Modeling financial time series by stochastic processes is a challenging task and a central area of research in financial mathematics. In this paper, we break through this barrier and present Quant GANs, a data-driven model which is inspired by the recent success of generative adversarial networks (GANs). Quant GANs consist of a generator and discriminator function which utilize temporal convolutional networks (TCNs) and thereby achieve to capture longer-ranging dependencies such as the presence of volatility clusters. Furthermore, the generator function is explicitly constructed such that the induced stochastic process allows a transition to its risk-neutral distribution. Our numerical results highlight that distributional properties for small and large lags are in an excellent agreement and dependence properties such as volatility clusters, leverage effects, and serial autocorrelations can be generated by the generator function of Quant GANs, demonstrably in high fidelity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge