Interpolation of Missing Swaption Volatility Data using Gibbs Sampling on Variational Autoencoders

Albeit of crucial interest for both financial practitioners and researchers, market-implied volatility data of European swaptions often exhibit large portions of missing quotes due to illiquidity of the various underlying swaption instruments. In this case, standard stochastic interpolation tools like the common SABR model often cannot be calibrated to observed implied volatility smiles, due to data being only available for the at-the-money quote of the respective underlying swaption. Here, we propose to infer the geometry of the full unknown implied volatility cube by learning stochastic latent representations of implied volatility cubes via variational autoencoders, enabling inference about the missing volatility data conditional on the observed data by an approximate Gibbs sampling approach. Imputed estimates of missing quotes can afterwards be used to fit a standard stochastic volatility model. Since training data for the employed variational autoencoder model is usually sparsely available, we test the robustness of the approach for a model trained on synthetic data on real market quotes and we show that SABR interpolated volatilites calibrated to reconstructed volatility cubes with artificially imputed missing values differ by not much more than two basis points compared to SABR fits calibrated to the complete cube. Moreover, we show how the imputation can be used to successfully set up delta-neutral portfolios for hedging purposes.

Estimating the Value-at-Risk by Temporal VAE

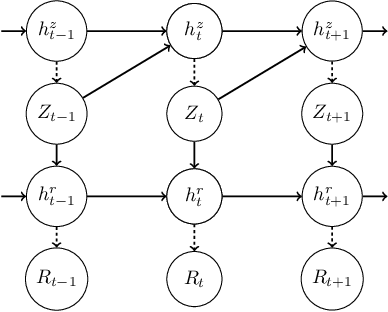
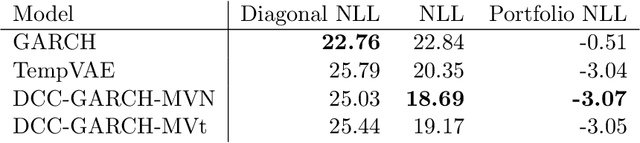
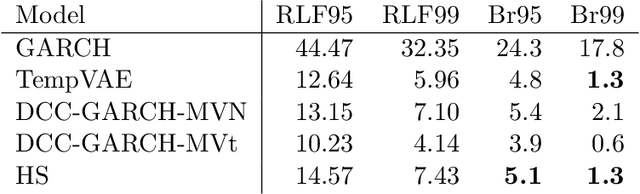
Estimation of the value-at-risk (VaR) of a large portfolio of assets is an important task for financial institutions. As the joint log-returns of asset prices can often be projected to a latent space of a much smaller dimension, the use of a variational autoencoder (VAE) for estimating the VaR is a natural suggestion. To ensure the bottleneck structure of autoencoders when learning sequential data, we use a temporal VAE (TempVAE) that avoids an auto-regressive structure for the observation variables. However, the low signal- to-noise ratio of financial data in combination with the auto-pruning property of a VAE typically makes the use of a VAE prone to posterior collapse. Therefore, we propose to use annealing of the regularization to mitigate this effect. As a result, the auto-pruning of the TempVAE works properly which also results in excellent estimation results for the VaR that beats classical GARCH-type and historical simulation approaches when applied to real data.