Estimating the Value-at-Risk by Temporal VAE

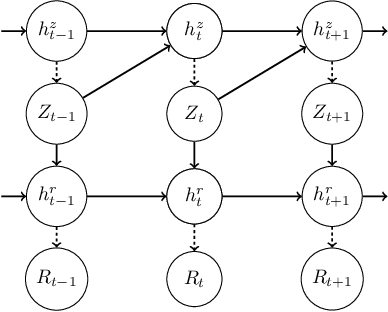
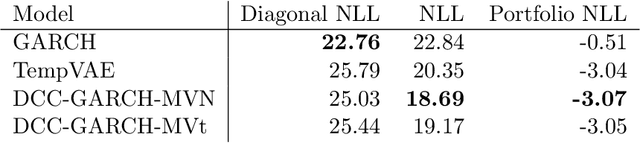
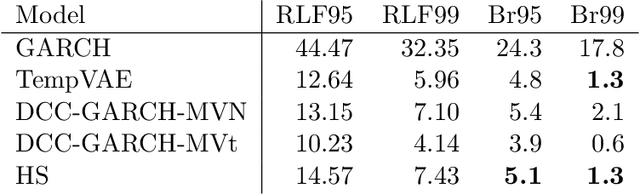
Estimation of the value-at-risk (VaR) of a large portfolio of assets is an important task for financial institutions. As the joint log-returns of asset prices can often be projected to a latent space of a much smaller dimension, the use of a variational autoencoder (VAE) for estimating the VaR is a natural suggestion. To ensure the bottleneck structure of autoencoders when learning sequential data, we use a temporal VAE (TempVAE) that avoids an auto-regressive structure for the observation variables. However, the low signal- to-noise ratio of financial data in combination with the auto-pruning property of a VAE typically makes the use of a VAE prone to posterior collapse. Therefore, we propose to use annealing of the regularization to mitigate this effect. As a result, the auto-pruning of the TempVAE works properly which also results in excellent estimation results for the VaR that beats classical GARCH-type and historical simulation approaches when applied to real data.

A Generalised Linear Model Framework for Variational Autoencoders based on Exponential Dispersion Families

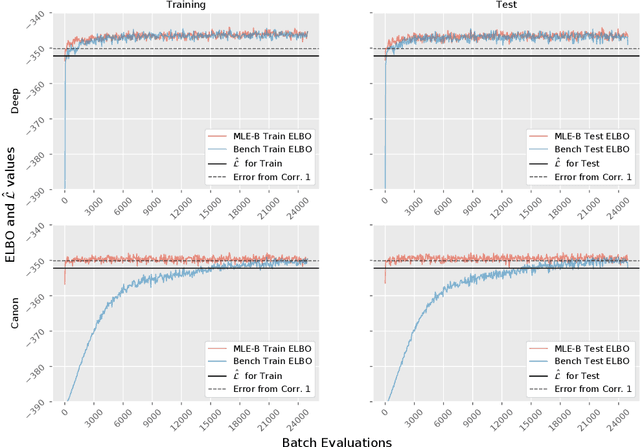
Although variational autoencoders (VAE) are successfully used to obtain meaningful low-dimensional representations for high-dimensional data, aspects of their loss function are not yet fully understood. We introduce a theoretical framework that is based on a connection between VAE and generalized linear models (GLM). The equality between the activation function of a VAE and the inverse of the link function of a GLM enables us to provide a systematic generalization of the loss analysis for VAE based on the assumption that the distribution of the decoder belongs to an exponential dispersion family (EDF). As a further result, we can initialize VAE nets by maximum likelihood estimates (MLE) that enhance the training performance on both synthetic and real world data sets.

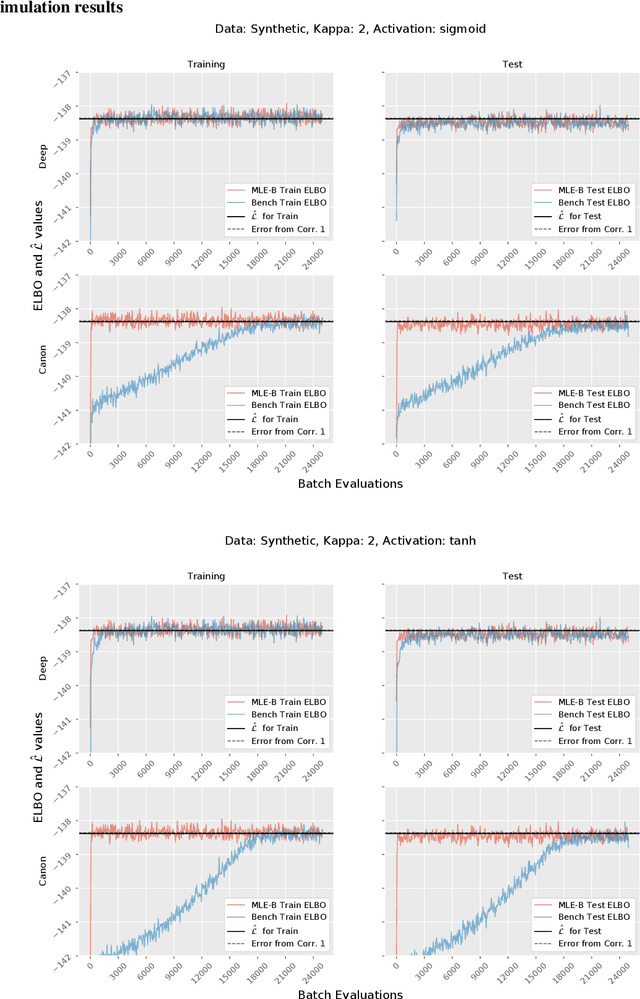
A lower bound for the ELBO of the Bernoulli Variational Autoencoder

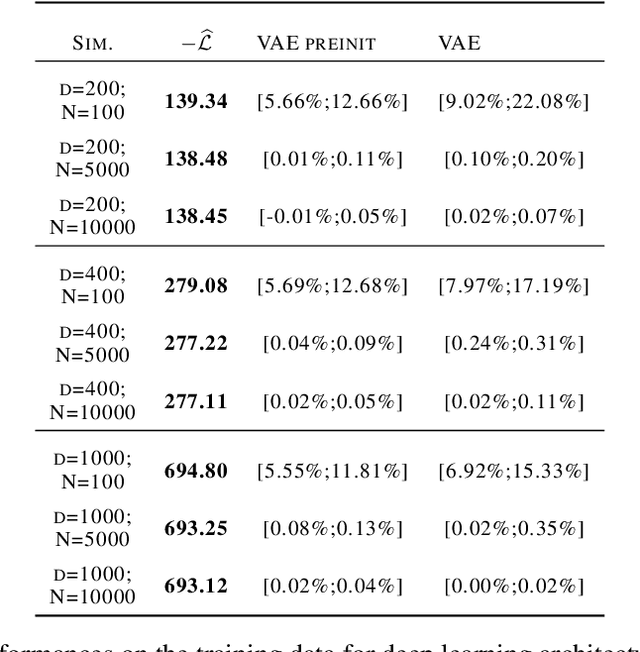
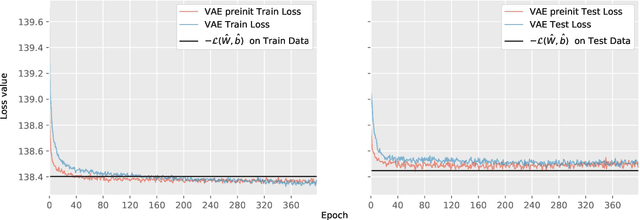
We consider a variational autoencoder (VAE) for binary data. Our main innovations are an interpretable lower bound for its training objective, a modified initialization and architecture of such a VAE that leads to faster training, and a decision support for finding the appropriate dimension of the latent space via using a PCA. Numerical examples illustrate our theoretical result and the performance of the new architecture.