Uncertainty-Aware Strategies: A Model-Agnostic Framework for Robust Financial Optimization through Subsampling

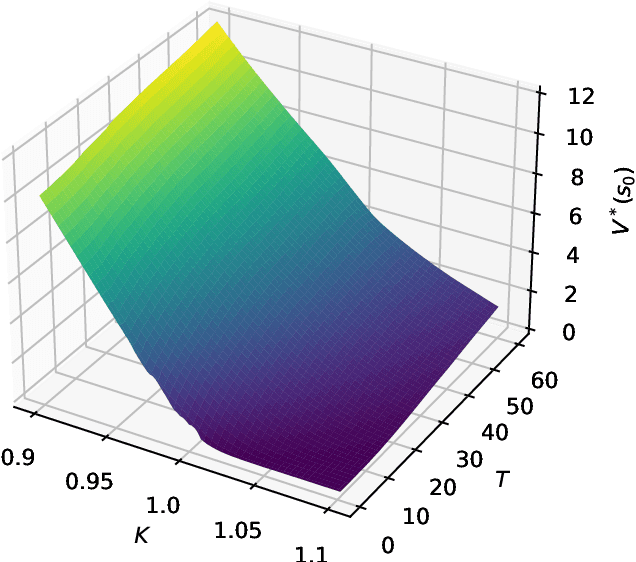
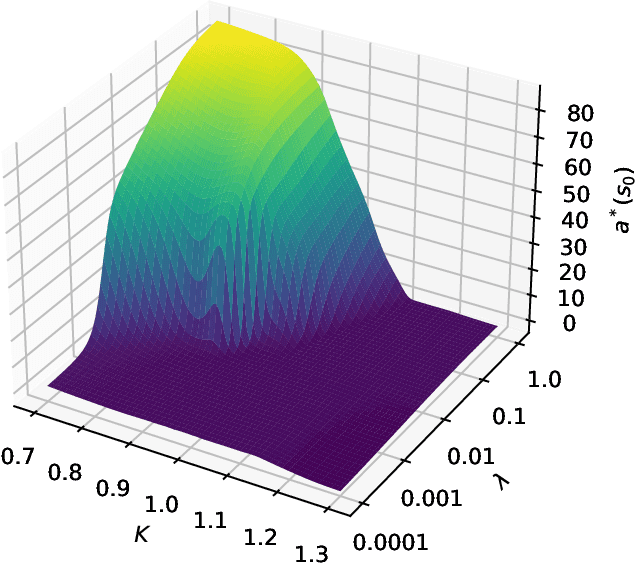
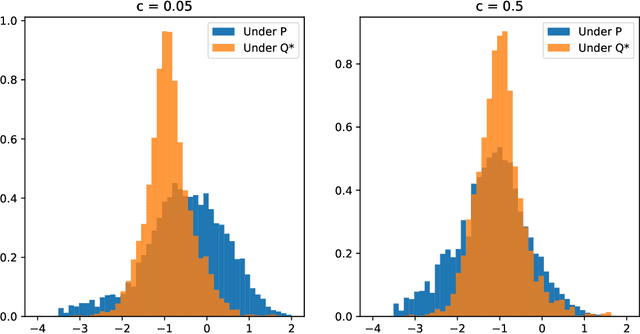
This paper addresses the challenge of model uncertainty in quantitative finance, where decisions in portfolio allocation, derivative pricing, and risk management rely on estimating stochastic models from limited data. In practice, the unavailability of the true probability measure forces reliance on an empirical approximation, and even small misestimations can lead to significant deviations in decision quality. Building on the framework of Klibanoff et al. (2005), we enhance the conventional objective - whether this is expected utility in an investing context or a hedging metric - by superimposing an outer "uncertainty measure", motivated by traditional monetary risk measures, on the space of models. In scenarios where a natural model distribution is lacking or Bayesian methods are impractical, we propose an ad hoc subsampling strategy, analogous to bootstrapping in statistical finance and related to mini-batch sampling in deep learning, to approximate model uncertainty. To address the quadratic memory demands of naive implementations, we also present an adapted stochastic gradient descent algorithm that enables efficient parallelization. Through analytical, simulated, and empirical studies - including multi-period, real data and high-dimensional examples - we demonstrate that uncertainty measures outperform traditional mixture of measures strategies and our model-agnostic subsampling-based approach not only enhances robustness against model risk but also achieves performance comparable to more elaborate Bayesian methods.

Deep Hedging: Continuous Reinforcement Learning for Hedging of General Portfolios across Multiple Risk Aversions

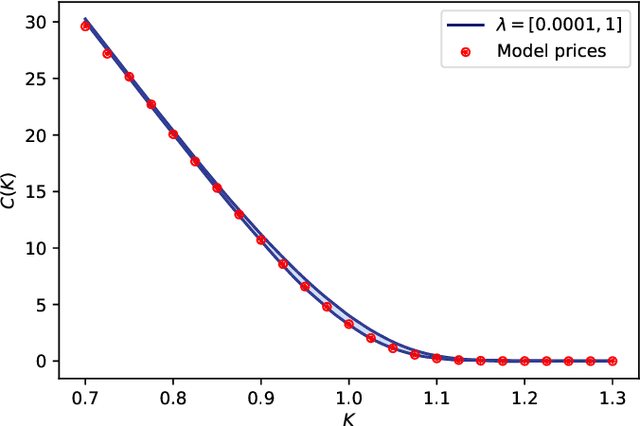
We present a method for finding optimal hedging policies for arbitrary initial portfolios and market states. We develop a novel actor-critic algorithm for solving general risk-averse stochastic control problems and use it to learn hedging strategies across multiple risk aversion levels simultaneously. We demonstrate the effectiveness of the approach with a numerical example in a stochastic volatility environment.

Multi-Asset Spot and Option Market Simulation

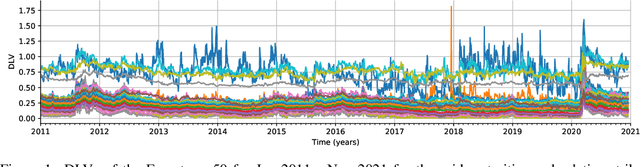
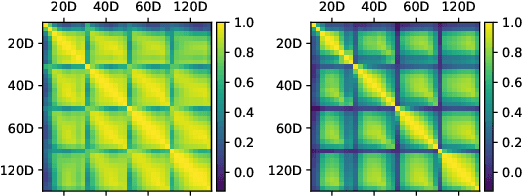
We construct realistic spot and equity option market simulators for a single underlying on the basis of normalizing flows. We address the high-dimensionality of market observed call prices through an arbitrage-free autoencoder that approximates efficient low-dimensional representations of the prices while maintaining no static arbitrage in the reconstructed surface. Given a multi-asset universe, we leverage the conditional invertibility property of normalizing flows and introduce a scalable method to calibrate the joint distribution of a set of independent simulators while preserving the dynamics of each simulator. Empirical results highlight the goodness of the calibrated simulators and their fidelity.

Deep Hedging: Learning to Remove the Drift under Trading Frictions with Minimal Equivalent Near-Martingale Measures

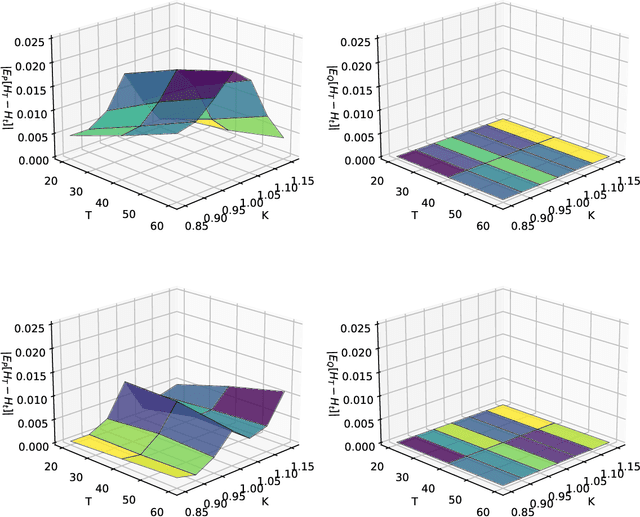
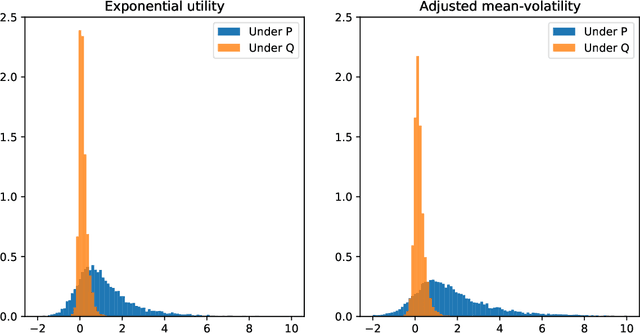
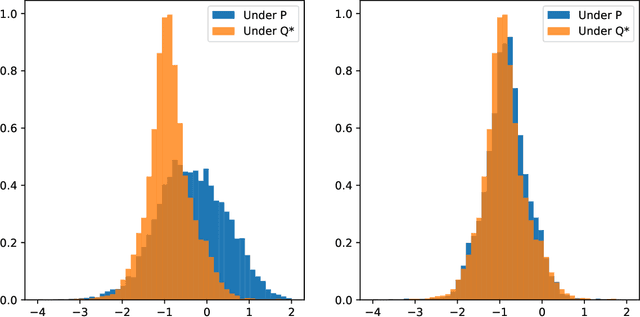
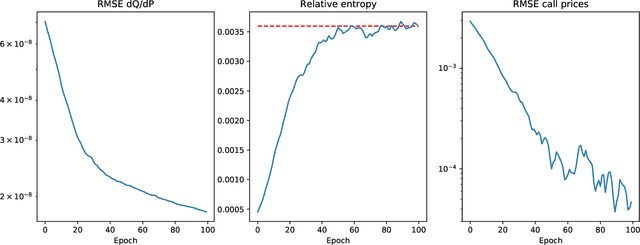
We present a numerically efficient approach for learning minimal equivalent martingale measures for market simulators of tradable instruments, e.g. for a spot price and options written on the same underlying. In the presence of transaction cost and trading restrictions, we relax the results to learning minimal equivalent "near-martingale measures" under which expected returns remain within prevailing bid/ask spreads. Our approach to thus "removing the drift" in a high dimensional complex space is entirely model-free and can be applied to any market simulator which does not exhibit classic arbitrage. The resulting model can be used for risk neutral pricing, or, in the case of transaction costs or trading constraints, for "Deep Hedging". We demonstrate our approach by applying it to two market simulators, an auto-regressive discrete-time stochastic implied volatility model, and a Generative Adversarial Network (GAN) based simulator, both of which trained on historical data of option prices under the statistical measure to produce realistic samples of spot and option prices. We comment on robustness with respect to estimation error of the original market simulator.

Deep Hedging: Learning Risk-Neutral Implied Volatility Dynamics

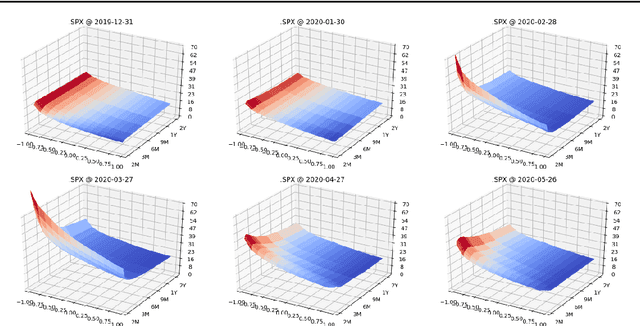
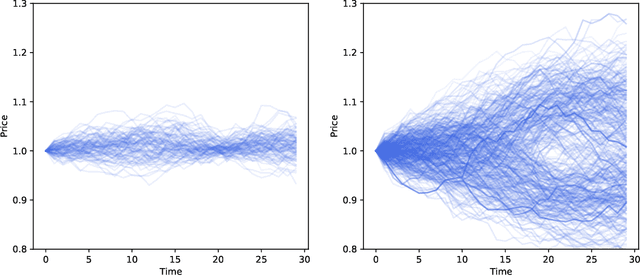
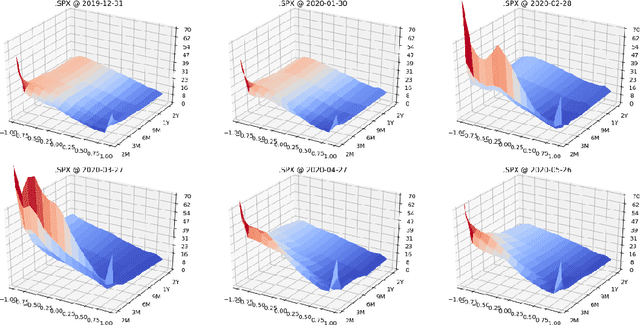
We present a numerically efficient approach for learning a risk-neutral measure for paths of simulated spot and option prices up to a finite horizon under convex transaction costs and convex trading constraints. This approach can then be used to implement a stochastic implied volatility model in the following two steps: 1. Train a market simulator for option prices, as discussed for example in our recent; 2. Find a risk-neutral density, specifically the minimal entropy martingale measure. The resulting model can be used for risk-neutral pricing, or for Deep Hedging in the case of transaction costs or trading constraints. To motivate the proposed approach, we also show that market dynamics are free from "statistical arbitrage" in the absence of transaction costs if and only if they follow a risk-neutral measure. We additionally provide a more general characterization in the presence of convex transaction costs and trading constraints. These results can be seen as an analogue of the fundamental theorem of asset pricing for statistical arbitrage under trading frictions and are of independent interest.

Deep Hedging: Learning to Simulate Equity Option Markets

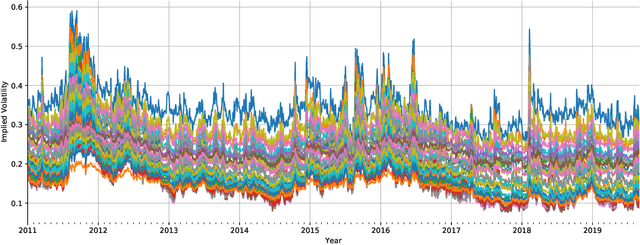
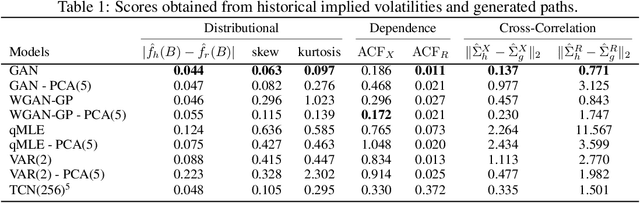
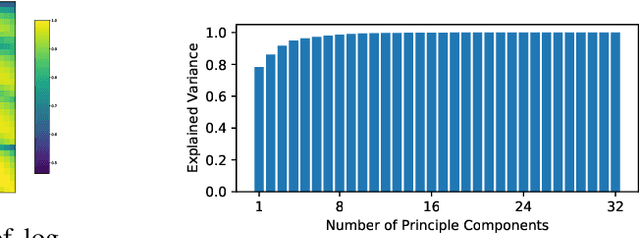
We construct realistic equity option market simulators based on generative adversarial networks (GANs). We consider recurrent and temporal convolutional architectures, and assess the impact of state compression. Option market simulators are highly relevant because they allow us to extend the limited real-world data sets available for the training and evaluation of option trading strategies. We show that network-based generators outperform classical methods on a range of benchmark metrics, and adversarial training achieves the best performance. Our work demonstrates for the first time that GANs can be successfully applied to the task of generating multivariate financial time series.