Nonparametric Filtering, Estimation and Classification using Neural Jump ODEs

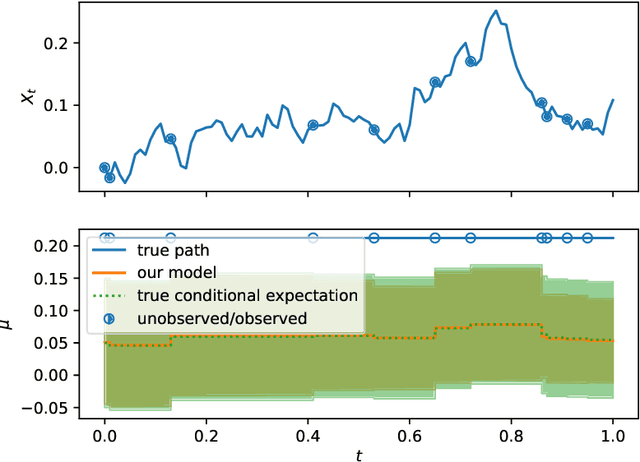
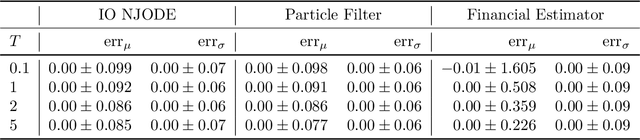
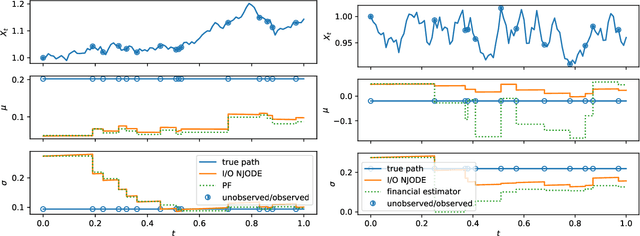
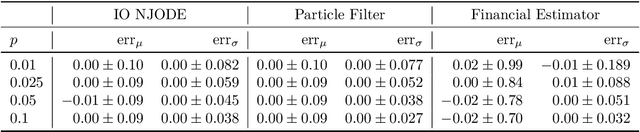
Neural Jump ODEs model the conditional expectation between observations by neural ODEs and jump at arrival of new observations. They have demonstrated effectiveness for fully data-driven online forecasting in settings with irregular and partial observations, operating under weak regularity assumptions. This work extends the framework to input-output systems, enabling direct applications in online filtering and classification. We establish theoretical convergence guarantees for this approach, providing a robust solution to $L^2$-optimal filtering. Empirical experiments highlight the model's superior performance over classical parametric methods, particularly in scenarios with complex underlying distributions. These results emphasise the approach's potential in time-sensitive domains such as finance and health monitoring, where real-time accuracy is crucial.

A Human-in-the-Loop Fairness-Aware Model Selection Framework for Complex Fairness Objective Landscapes

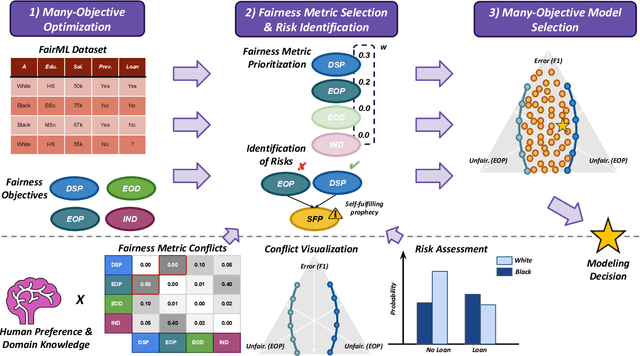
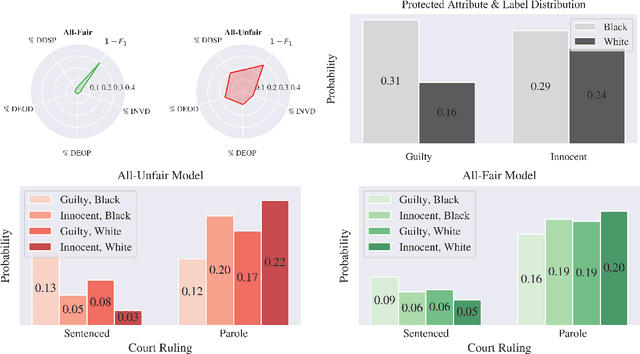
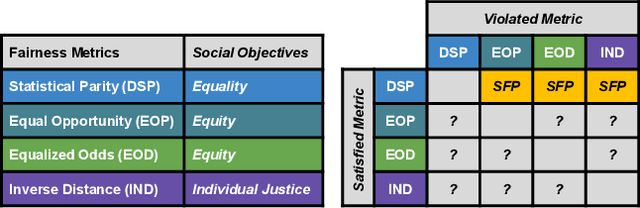
Fairness-aware Machine Learning (FairML) applications are often characterized by complex social objectives and legal requirements, frequently involving multiple, potentially conflicting notions of fairness. Despite the well-known Impossibility Theorem of Fairness and extensive theoretical research on the statistical and socio-technical trade-offs between fairness metrics, many FairML tools still optimize or constrain for a single fairness objective. However, this one-sided optimization can inadvertently lead to violations of other relevant notions of fairness. In this socio-technical and empirical study, we frame fairness as a many-objective (MaO) problem by treating fairness metrics as conflicting objectives. We introduce ManyFairHPO, a human-in-the-loop, fairness-aware model selection framework that enables practitioners to effectively navigate complex and nuanced fairness objective landscapes. ManyFairHPO aids in the identification, evaluation, and balancing of fairness metric conflicts and their related social consequences, leading to more informed and socially responsible model-selection decisions. Through a comprehensive empirical evaluation and a case study on the Law School Admissions problem, we demonstrate the effectiveness of ManyFairHPO in balancing multiple fairness objectives, mitigating risks such as self-fulfilling prophecies, and providing interpretable insights to guide stakeholders in making fairness-aware modeling decisions.

The Unfairness of $\varepsilon$-Fairness

Fairness in decision-making processes is often quantified using probabilistic metrics. However, these metrics may not fully capture the real-world consequences of unfairness. In this article, we adopt a utility-based approach to more accurately measure the real-world impacts of decision-making process. In particular, we show that if the concept of $\varepsilon$-fairness is employed, it can possibly lead to outcomes that are maximally unfair in the real-world context. Additionally, we address the common issue of unavailable data on false negatives by proposing a reduced setting that still captures essential fairness considerations. We illustrate our findings with two real-world examples: college admissions and credit risk assessment. Our analysis reveals that while traditional probability-based evaluations might suggest fairness, a utility-based approach uncovers the necessary actions to truly achieve equality. For instance, in the college admission case, we find that enhancing completion rates is crucial for ensuring fairness. Summarizing, this paper highlights the importance of considering the real-world context when evaluating fairness.

Estimating value at risk: LSTM vs. GARCH

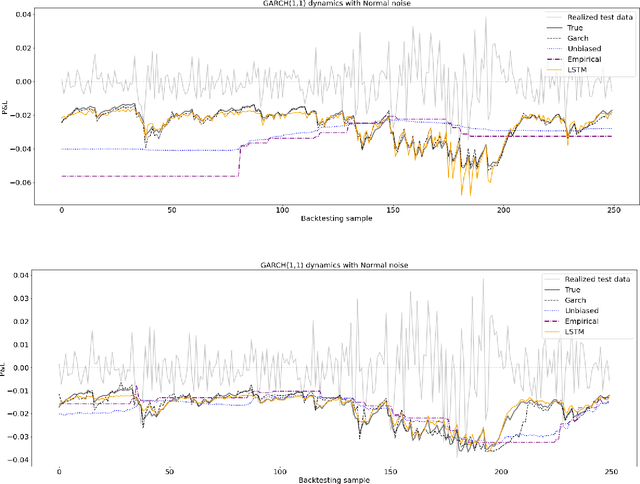
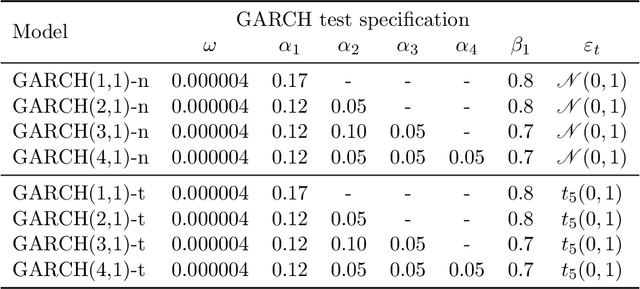
Estimating value-at-risk on time series data with possibly heteroscedastic dynamics is a highly challenging task. Typically, we face a small data problem in combination with a high degree of non-linearity, causing difficulties for both classical and machine-learning estimation algorithms. In this paper, we propose a novel value-at-risk estimator using a long short-term memory (LSTM) neural network and compare its performance to benchmark GARCH estimators. Our results indicate that even for a relatively short time series, the LSTM could be used to refine or monitor risk estimation processes and correctly identify the underlying risk dynamics in a non-parametric fashion. We evaluate the estimator on both simulated and market data with a focus on heteroscedasticity, finding that LSTM exhibits a similar performance to GARCH estimators on simulated data, whereas on real market data it is more sensitive towards increasing or decreasing volatility and outperforms all existing estimators of value-at-risk in terms of exception rate and mean quantile score.

Deep dynamic modeling with just two time points: Can we still allow for individual trajectories?

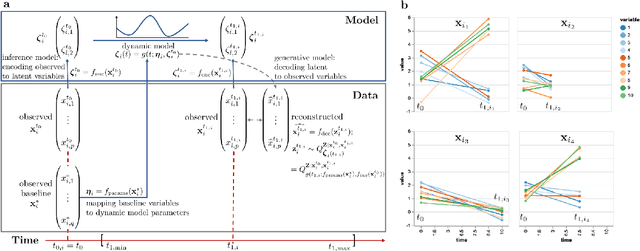
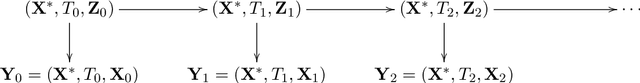
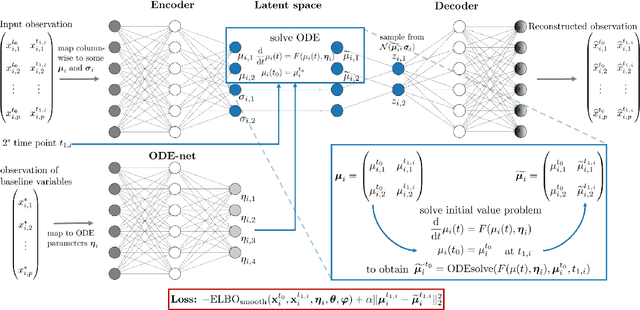
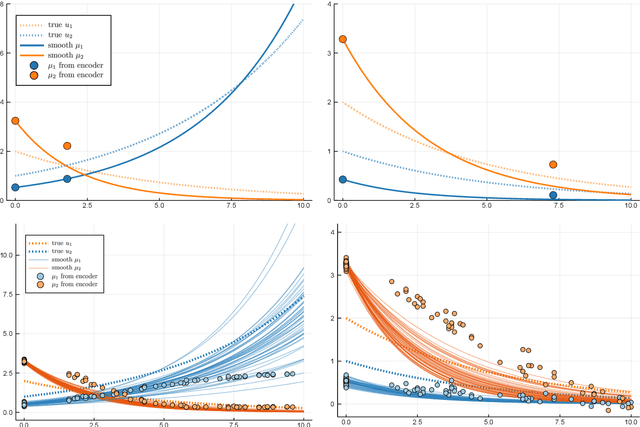
Longitudinal biomedical data are often characterized by a sparse time grid and individual-specific development patterns. Specifically, in epidemiological cohort studies and clinical registries we are facing the question of what can be learned from the data in an early phase of the study, when only a baseline characterization and one follow-up measurement are available. Inspired by recent advances that allow to combine deep learning with dynamic modeling, we investigate whether such approaches can be useful for uncovering complex structure, in particular for an extreme small data setting with only two observations time points for each individual. Irregular spacing in time could then be used to gain more information on individual dynamics by leveraging similarity of individuals. We provide a brief overview of how variational autoencoders (VAEs), as a deep learning approach, can be linked to ordinary differential equations (ODEs) for dynamic modeling, and then specifically investigate the feasibility of such an approach that infers individual-specific latent trajectories by including regularity assumptions and individuals' similarity. We also provide a description of this deep learning approach as a filtering task to give a statistical perspective. Using simulated data, we show to what extent the approach can recover individual trajectories from ODE systems with two and four unknown parameters and infer groups of individuals with similar trajectories, and where it breaks down. The results show that such dynamic deep learning approaches can be useful even in extreme small data settings, but need to be carefully adapted.

Machine learning for multiple yield curve markets: fast calibration in the Gaussian affine framework

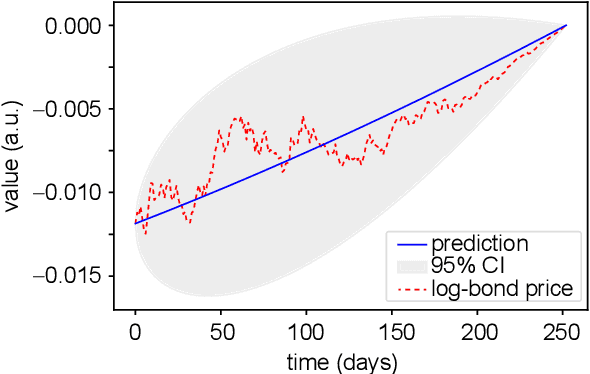
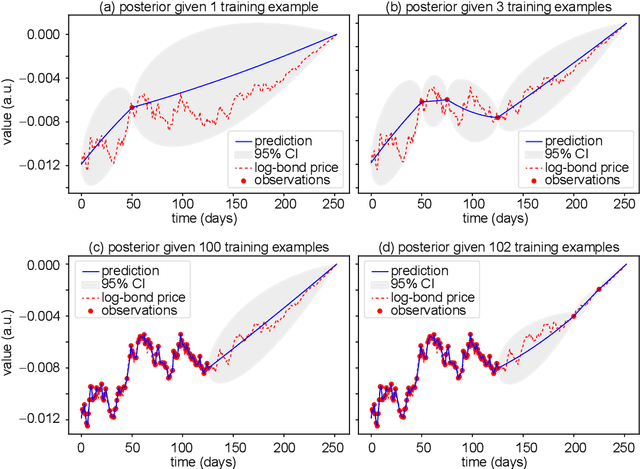
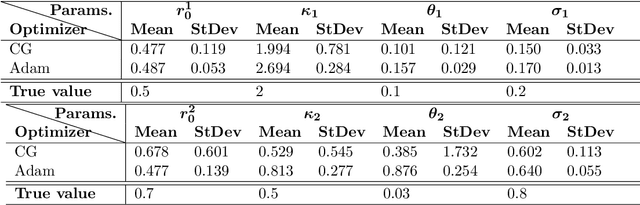
Calibration is a highly challenging task, in particular in multiple yield curve markets. This paper is a first attempt to study the chances and challenges of the application of machine learning techniques for this. We employ Gaussian process regression, a machine learning methodology having many similarities with extended Kalman filtering - a technique which has been applied many times to interest rate markets and term structure models. We find very good results for the single curve markets and many challenges for the multi curve markets in a Vasicek framework. The Gaussian process regression is implemented with the Adam optimizer and the non-linear conjugate gradient method, where the latter performs best. We also point towards future research.