Nonparametric Filtering, Estimation and Classification using Neural Jump ODEs

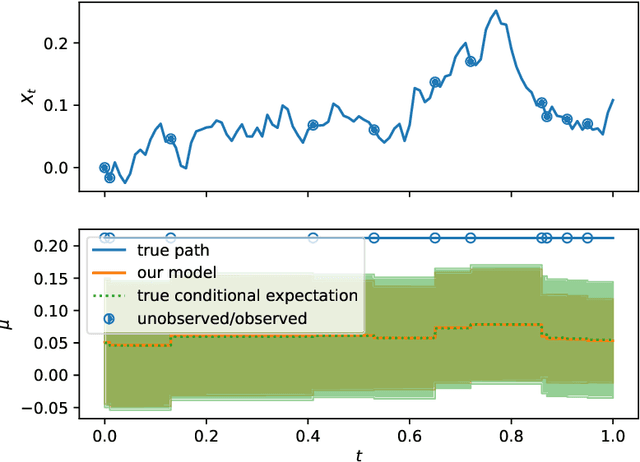
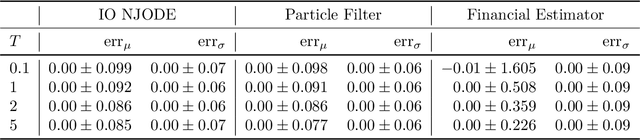
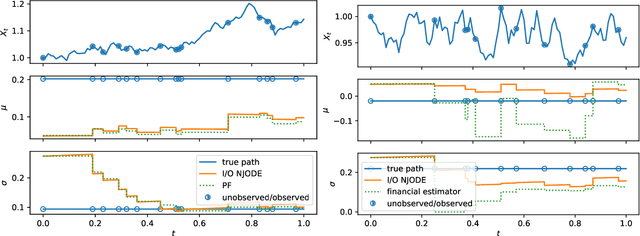
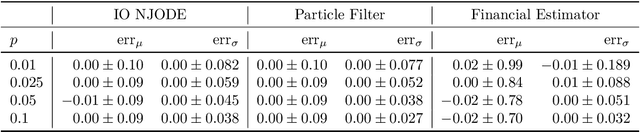
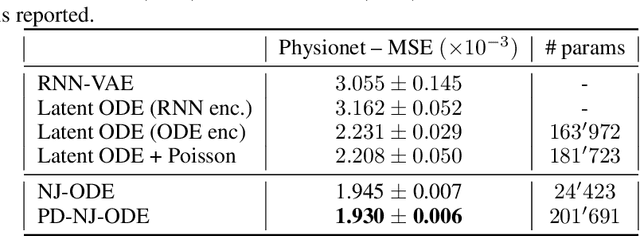
Neural Jump ODEs model the conditional expectation between observations by neural ODEs and jump at arrival of new observations. They have demonstrated effectiveness for fully data-driven online forecasting in settings with irregular and partial observations, operating under weak regularity assumptions. This work extends the framework to input-output systems, enabling direct applications in online filtering and classification. We establish theoretical convergence guarantees for this approach, providing a robust solution to $L^2$-optimal filtering. Empirical experiments highlight the model's superior performance over classical parametric methods, particularly in scenarios with complex underlying distributions. These results emphasise the approach's potential in time-sensitive domains such as finance and health monitoring, where real-time accuracy is crucial.

Learning Chaotic Systems and Long-Term Predictions with Neural Jump ODEs

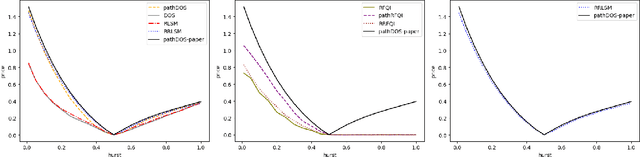
The Path-dependent Neural Jump ODE (PD-NJ-ODE) is a model for online prediction of generic (possibly non-Markovian) stochastic processes with irregular (in time) and potentially incomplete (with respect to coordinates) observations. It is a model for which convergence to the $L^2$-optimal predictor, which is given by the conditional expectation, is established theoretically. Thereby, the training of the model is solely based on a dataset of realizations of the underlying stochastic process, without the need of knowledge of the law of the process. In the case where the underlying process is deterministic, the conditional expectation coincides with the process itself. Therefore, this framework can equivalently be used to learn the dynamics of ODE or PDE systems solely from realizations of the dynamical system with different initial conditions. We showcase the potential of our method by applying it to the chaotic system of a double pendulum. When training the standard PD-NJ-ODE method, we see that the prediction starts to diverge from the true path after about half of the evaluation time. In this work we enhance the model with two novel ideas, which independently of each other improve the performance of our modelling setup. The resulting dynamics match the true dynamics of the chaotic system very closely. The same enhancements can be used to provably enable the PD-NJ-ODE to learn long-term predictions for general stochastic datasets, where the standard model fails. This is verified in several experiments.

Filtered not Mixed: Stochastic Filtering-Based Online Gating for Mixture of Large Language Models

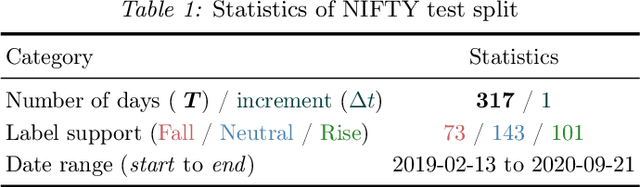
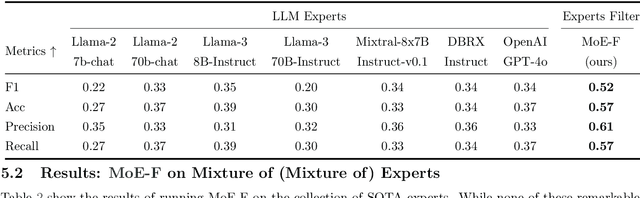
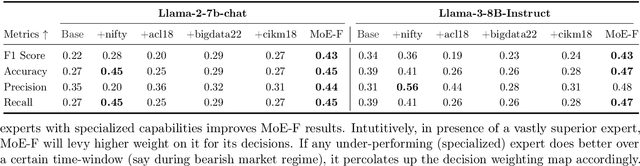
We propose MoE-F -- a formalised mechanism for combining $N$ pre-trained expert Large Language Models (LLMs) in online time-series prediction tasks by adaptively forecasting the best weighting of LLM predictions at every time step. Our mechanism leverages the conditional information in each expert's running performance to forecast the best combination of LLMs for predicting the time series in its next step. Diverging from static (learned) Mixture of Experts (MoE) methods, MoE-F employs time-adaptive stochastic filtering techniques to combine experts. By framing the expert selection problem as a finite state-space, continuous-time Hidden Markov model (HMM), we can leverage the Wohman-Shiryaev filter. Our approach first constructs $N$ parallel filters corresponding to each of the $N$ individual LLMs. Each filter proposes its best combination of LLMs, given the information that they have access to. Subsequently, the $N$ filter outputs are aggregated to optimize a lower bound for the loss of the aggregated LLMs, which can be optimized in closed-form, thus generating our ensemble predictor. Our contributions here are: (I) the MoE-F algorithm -- deployable as a plug-and-play filtering harness, (II) theoretical optimality guarantees of the proposed filtering-based gating algorithm, and (III) empirical evaluation and ablative results using state of the art foundational and MoE LLMs on a real-world Financial Market Movement task where MoE-F attains a remarkable 17% absolute and 48.5% relative F1 measure improvement over the next best performing individual LLM expert.

Robust Utility Optimization via a GAN Approach

Robust utility optimization enables an investor to deal with market uncertainty in a structured way, with the goal of maximizing the worst-case outcome. In this work, we propose a generative adversarial network (GAN) approach to (approximately) solve robust utility optimization problems in general and realistic settings. In particular, we model both the investor and the market by neural networks (NN) and train them in a mini-max zero-sum game. This approach is applicable for any continuous utility function and in realistic market settings with trading costs, where only observable information of the market can be used. A large empirical study shows the versatile usability of our method. Whenever an optimal reference strategy is available, our method performs on par with it and in the (many) settings without known optimal strategy, our method outperforms all other reference strategies. Moreover, we can conclude from our study that the trained path-dependent strategies do not outperform Markovian ones. Lastly, we uncover that our generative approach for learning optimal, (non-) robust investments under trading costs generates universally applicable alternatives to well known asymptotic strategies of idealized settings.

Regret-Optimal Federated Transfer Learning for Kernel Regression with Applications in American Option Pricing

We propose an optimal iterative scheme for federated transfer learning, where a central planner has access to datasets ${\cal D}_1,\dots,{\cal D}_N$ for the same learning model $f_{\theta}$. Our objective is to minimize the cumulative deviation of the generated parameters $\{\theta_i(t)\}_{t=0}^T$ across all $T$ iterations from the specialized parameters $\theta^\star_{1},\ldots,\theta^\star_N$ obtained for each dataset, while respecting the loss function for the model $f_{\theta(T)}$ produced by the algorithm upon halting. We only allow for continual communication between each of the specialized models (nodes/agents) and the central planner (server), at each iteration (round). For the case where the model $f_{\theta}$ is a finite-rank kernel regression, we derive explicit updates for the regret-optimal algorithm. By leveraging symmetries within the regret-optimal algorithm, we further develop a nearly regret-optimal heuristic that runs with $\mathcal{O}(Np^2)$ fewer elementary operations, where $p$ is the dimension of the parameter space. Additionally, we investigate the adversarial robustness of the regret-optimal algorithm showing that an adversary which perturbs $q$ training pairs by at-most $\varepsilon>0$, across all training sets, cannot reduce the regret-optimal algorithm's regret by more than $\mathcal{O}(\varepsilon q \bar{N}^{1/2})$, where $\bar{N}$ is the aggregate number of training pairs. To validate our theoretical findings, we conduct numerical experiments in the context of American option pricing, utilizing a randomly generated finite-rank kernel.

Extending Path-Dependent NJ-ODEs to Noisy Observations and a Dependent Observation Framework

The Path-Dependent Neural Jump ODE (PD-NJ-ODE) is a model for predicting continuous-time stochastic processes with irregular and incomplete observations. In particular, the method learns optimal forecasts given irregularly sampled time series of incomplete past observations. So far the process itself and the coordinate-wise observation times were assumed to be independent and observations were assumed to be noiseless. In this work we discuss two extensions to lift these restrictions and provide theoretical guarantees as well as empirical examples for them.

Optimal Estimation of Generic Dynamics by Path-Dependent Neural Jump ODEs

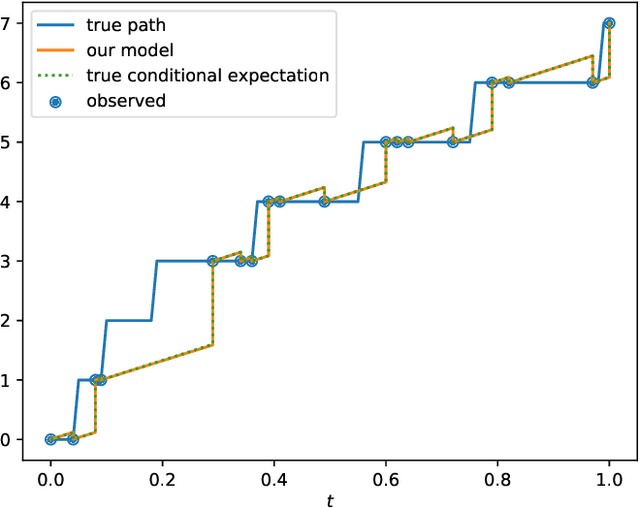
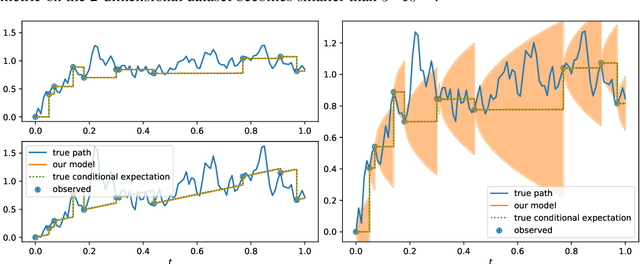
This paper studies the problem of forecasting general stochastic processes using an extension of the Neural Jump ODE (NJ-ODE) framework. While NJ-ODE was the first framework to establish convergence guarantees for the prediction of irregularly observed time-series, these results were limited to data stemming from It\^o-diffusions with complete observations, in particular Markov processes where all coordinates are observed simultaneously. In this work, we generalise these results to generic, possibly non-Markovian or discontinuous, stochastic processes with incomplete observations, by utilising the reconstruction properties of the signature transform. These theoretical results are supported by empirical studies, where it is shown that the path-dependent NJ-ODE outperforms the original NJ-ODE framework in the case of non-Markovian data.

Optimal Stopping via Randomized Neural Networks

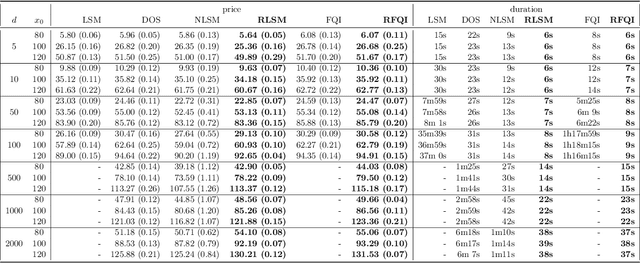
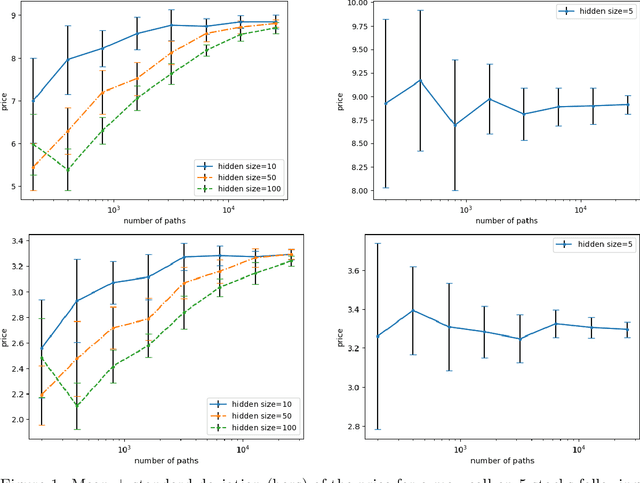
This paper presents new machine learning approaches to approximate the solution of optimal stopping problems. The key idea of these methods is to use neural networks, where the hidden layers are generated randomly and only the last layer is trained, in order to approximate the continuation value. Our approaches are applicable for high dimensional problems where the existing approaches become increasingly impractical. In addition, since our approaches can be optimized using a simple linear regression, they are very easy to implement and theoretical guarantees can be provided. In Markovian examples our randomized reinforcement learning approach and in non-Markovian examples our randomized recurrent neural network approach outperform the state-of-the-art and other relevant machine learning approaches.

Theoretical Guarantees for Learning Conditional Expectation using Controlled ODE-RNN

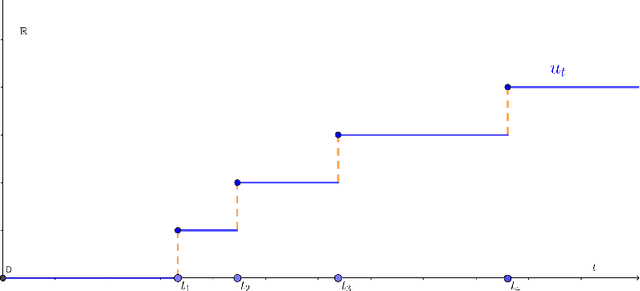
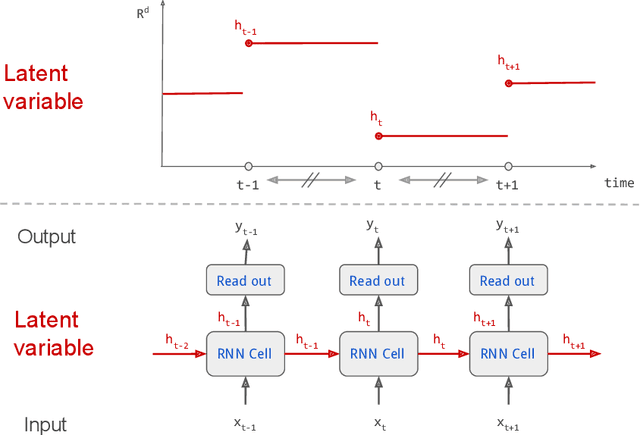
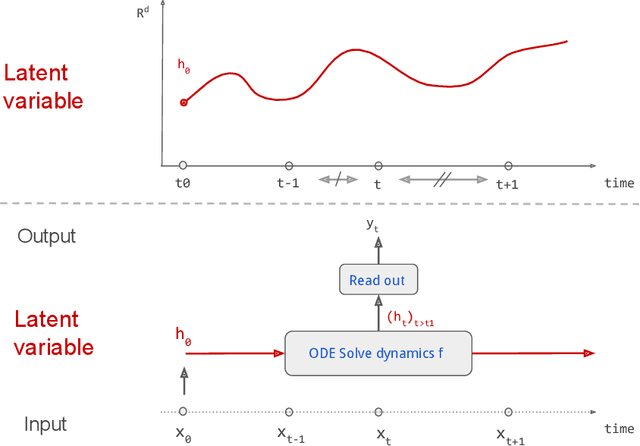
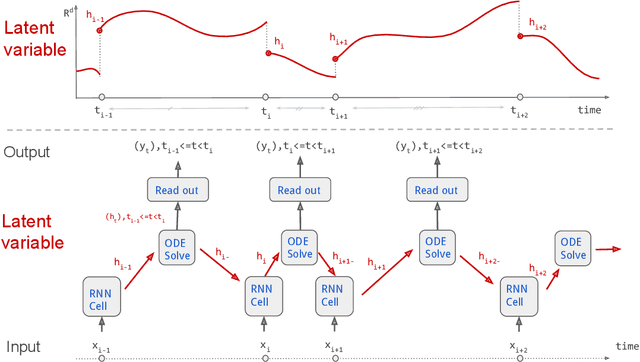
Continuous stochastic processes are widely used to model time series that exhibit a random behaviour. Predictions of the stochastic process can be computed by the conditional expectation given the current information. To this end, we introduce the controlled ODE-RNN that provides a data-driven approach to learn the conditional expectation of a stochastic process. Our approach extends the ODE-RNN framework which models the latent state of a recurrent neural network (RNN) between two observations with a neural ordinary differential equation (neural ODE). We show that controlled ODEs provide a general framework which can in particular describe the ODE-RNN, combining in a single equation the continuous neural ODE part with the jumps introduced by RNN. We demonstrate the predictive capabilities of this model by proving that, under some regularities assumptions, the output process converges to the conditional expectation process.

Denise: Deep Learning based Robust PCA for Positive Semidefinite Matrices

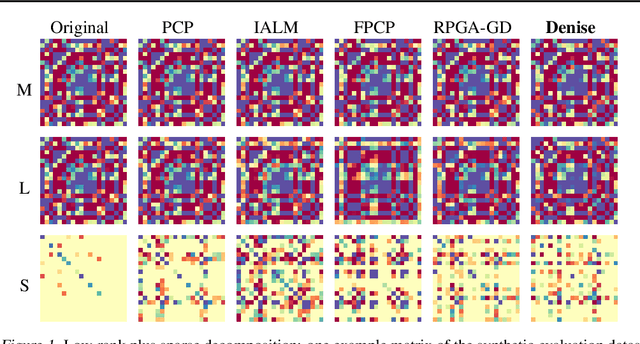
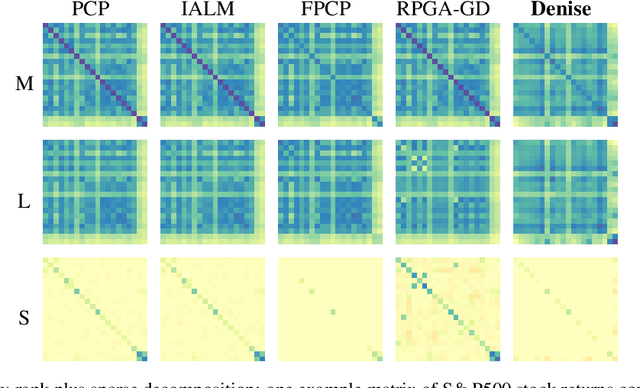
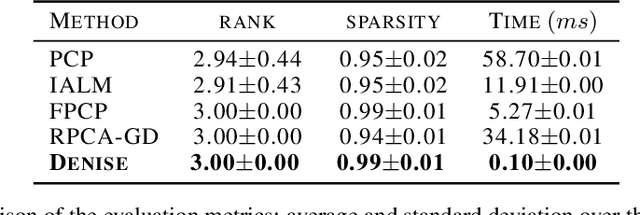
We introduce Denise, a deep learning based algorithm for decomposing positive semidefinite matrices into the sum of a low rank plus a sparse matrix. The deep neural network is trained on a randomly generated dataset using the Cholesky factorization. This method, benchmarked on synthetic datasets as well as on some S&P500 stock returns covariance matrices, achieves comparable results to several state-of-the-art techniques, while outperforming all existing algorithms in terms of computational time. Finally, theoretical results concerning the convergence of the training are derived.