Scalable Signature-Based Distribution Regression via Reference Sets

Distribution Regression (DR) on stochastic processes describes the learning task of regression on collections of time series. Path signatures, a technique prevalent in stochastic analysis, have been used to solve the DR problem. Recent works have demonstrated the ability of such solutions to leverage the information encoded in paths via signature-based features. However, current state of the art DR solutions are memory intensive and incur a high computation cost. This leads to a trade-off between path length and the number of paths considered. This computational bottleneck limits the application to small sample sizes which consequently introduces estimation uncertainty. In this paper, we present a methodology for addressing the above issues; resolving estimation uncertainties whilst also proposing a pipeline that enables us to use DR for a wide variety of learning tasks. Integral to our approach is our novel distance approximator. This allows us to seamlessly apply our methodology across different application domains, sampling rates, and stochastic process dimensions. We show that our model performs well in applications related to estimation theory, quantitative finance, and physical sciences. We demonstrate that our model generalises well, not only to unseen data within a given distribution, but also under unseen regimes (unseen classes of stochastic models).

Filtered not Mixed: Stochastic Filtering-Based Online Gating for Mixture of Large Language Models

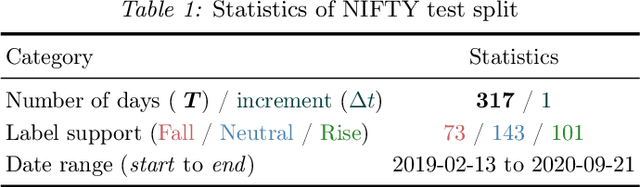
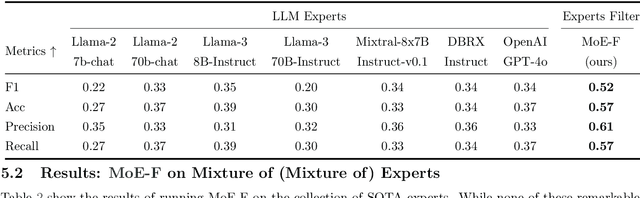
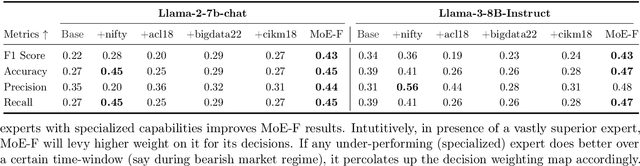
We propose MoE-F -- a formalised mechanism for combining $N$ pre-trained expert Large Language Models (LLMs) in online time-series prediction tasks by adaptively forecasting the best weighting of LLM predictions at every time step. Our mechanism leverages the conditional information in each expert's running performance to forecast the best combination of LLMs for predicting the time series in its next step. Diverging from static (learned) Mixture of Experts (MoE) methods, MoE-F employs time-adaptive stochastic filtering techniques to combine experts. By framing the expert selection problem as a finite state-space, continuous-time Hidden Markov model (HMM), we can leverage the Wohman-Shiryaev filter. Our approach first constructs $N$ parallel filters corresponding to each of the $N$ individual LLMs. Each filter proposes its best combination of LLMs, given the information that they have access to. Subsequently, the $N$ filter outputs are aggregated to optimize a lower bound for the loss of the aggregated LLMs, which can be optimized in closed-form, thus generating our ensemble predictor. Our contributions here are: (I) the MoE-F algorithm -- deployable as a plug-and-play filtering harness, (II) theoretical optimality guarantees of the proposed filtering-based gating algorithm, and (III) empirical evaluation and ablative results using state of the art foundational and MoE LLMs on a real-world Financial Market Movement task where MoE-F attains a remarkable 17% absolute and 48.5% relative F1 measure improvement over the next best performing individual LLM expert.

Reality Only Happens Once: Single-Path Generalization Bounds for Transformers

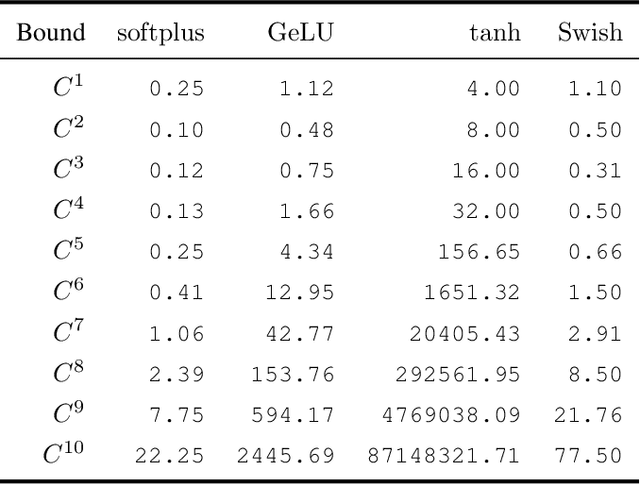
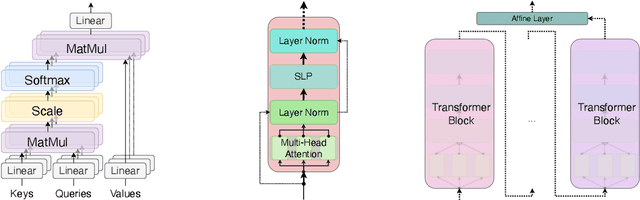
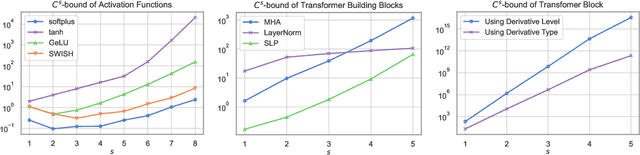
One of the inherent challenges in deploying transformers on time series is that \emph{reality only happens once}; namely, one typically only has access to a single trajectory of the data-generating process comprised of non-i.i.d. observations. We derive non-asymptotic statistical guarantees in this setting through bounds on the \textit{generalization} of a transformer network at a future-time $t$, given that it has been trained using $N\le t$ observations from a single perturbed trajectory of a Markov process. Under the assumption that the Markov process satisfies a log-Sobolev inequality, we obtain a generalization bound which effectively converges at the rate of ${O}(1/\sqrt{N})$. Our bound depends explicitly on the activation function ($\operatorname{Swish}$, $\operatorname{GeLU}$, or $\tanh$ are considered), the number of self-attention heads, depth, width, and norm-bounds defining the transformer architecture. Our bound consists of three components: (I) The first quantifies the gap between the stationary distribution of the data-generating Markov process and its distribution at time $t$, this term converges exponentially to $0$. (II) The next term encodes the complexity of the transformer model and, given enough time, eventually converges to $0$ at the rate ${O}(\log(N)^r/\sqrt{N})$ for any $r>0$. (III) The third term guarantees that the bound holds with probability at least $1$-$\delta$, and converges at a rate of ${O}(\sqrt{\log(1/\delta)}/\sqrt{N})$.

Non-parametric online market regime detection and regime clustering for multidimensional and path-dependent data structures

In this work we present a non-parametric online market regime detection method for multidimensional data structures using a path-wise two-sample test derived from a maximum mean discrepancy-based similarity metric on path space that uses rough path signatures as a feature map. The latter similarity metric has been developed and applied as a discriminator in recent generative models for small data environments, and has been optimised here to the setting where the size of new incoming data is particularly small, for faster reactivity. On the same principles, we also present a path-wise method for regime clustering which extends our previous work. The presented regime clustering techniques were designed as ex-ante market analysis tools that can identify periods of approximatively similar market activity, but the new results also apply to path-wise, high dimensional-, and to non-Markovian settings as well as to data structures that exhibit autocorrelation. We demonstrate our clustering tools on easily verifiable synthetic datasets of increasing complexity, and also show how the outlined regime detection techniques can be used as fast on-line automatic regime change detectors or as outlier detection tools, including a fully automated pipeline. Finally, we apply the fine-tuned algorithms to real-world historical data including high-dimensional baskets of equities and the recent price evolution of crypto assets, and we show that our methodology swiftly and accurately indicated historical periods of market turmoil.

Non-adversarial training of Neural SDEs with signature kernel scores

Neural SDEs are continuous-time generative models for sequential data. State-of-the-art performance for irregular time series generation has been previously obtained by training these models adversarially as GANs. However, as typical for GAN architectures, training is notoriously unstable, often suffers from mode collapse, and requires specialised techniques such as weight clipping and gradient penalty to mitigate these issues. In this paper, we introduce a novel class of scoring rules on pathspace based on signature kernels and use them as objective for training Neural SDEs non-adversarially. By showing strict properness of such kernel scores and consistency of the corresponding estimators, we provide existence and uniqueness guarantees for the minimiser. With this formulation, evaluating the generator-discriminator pair amounts to solving a system of linear path-dependent PDEs which allows for memory-efficient adjoint-based backpropagation. Moreover, because the proposed kernel scores are well-defined for paths with values in infinite dimensional spaces of functions, our framework can be easily extended to generate spatiotemporal data. Our procedure permits conditioning on a rich variety of market conditions and significantly outperforms alternative ways of training Neural SDEs on a variety of tasks including the simulation of rough volatility models, the conditional probabilistic forecasts of real-world forex pairs where the conditioning variable is an observed past trajectory, and the mesh-free generation of limit order book dynamics.

Clustering Market Regimes using the Wasserstein Distance

The problem of rapid and automated detection of distinct market regimes is a topic of great interest to financial mathematicians and practitioners alike. In this paper, we outline an unsupervised learning algorithm for clustering financial time-series into a suitable number of temporal segments (market regimes). As a special case of the above, we develop a robust algorithm that automates the process of classifying market regimes. The method is robust in the sense that it does not depend on modelling assumptions of the underlying time series as our experiments with real datasets show. This method -- dubbed the Wasserstein $k$-means algorithm -- frames such a problem as one on the space of probability measures with finite $p^\text{th}$ moment, in terms of the $p$-Wasserstein distance between (empirical) distributions. We compare our WK-means approach with a more traditional clustering algorithms by studying the so-called maximum mean discrepancy scores between, and within clusters. In both cases it is shown that the WK-means algorithm vastly outperforms all considered competitor approaches. We demonstrate the performance of all approaches both in a controlled environment on synthetic data, and on real data.

A Data-driven Market Simulator for Small Data Environments

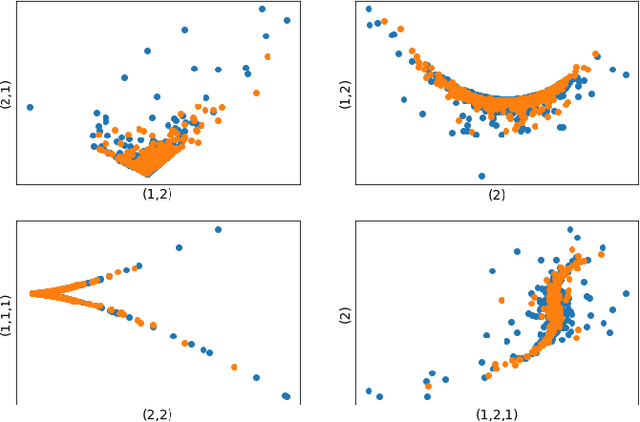
Neural network based data-driven market simulation unveils a new and flexible way of modelling financial time series without imposing assumptions on the underlying stochastic dynamics. Though in this sense generative market simulation is model-free, the concrete modelling choices are nevertheless decisive for the features of the simulated paths. We give a brief overview of currently used generative modelling approaches and performance evaluation metrics for financial time series, and address some of the challenges to achieve good results in the latter. We also contrast some classical approaches of market simulation with simulation based on generative modelling and highlight some advantages and pitfalls of the new approach. While most generative models tend to rely on large amounts of training data, we present here a generative model that works reliably in environments where the amount of available training data is notoriously small. Furthermore, we show how a rough paths perspective combined with a parsimonious Variational Autoencoder framework provides a powerful way for encoding and evaluating financial time series in such environments where available training data is scarce. Finally, we also propose a suitable performance evaluation metric for financial time series and discuss some connections of our Market Generator to deep hedging.