Filtered not Mixed: Stochastic Filtering-Based Online Gating for Mixture of Large Language Models
Paper and Code
Jun 05, 2024
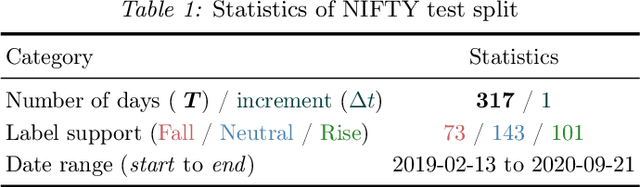
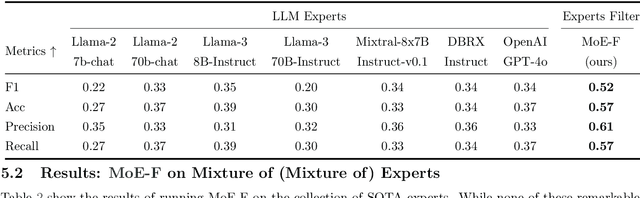
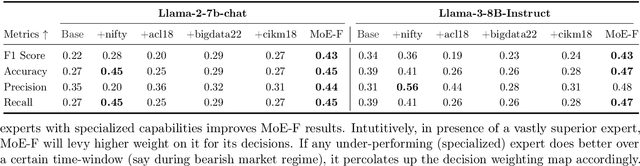
We propose MoE-F -- a formalised mechanism for combining $N$ pre-trained expert Large Language Models (LLMs) in online time-series prediction tasks by adaptively forecasting the best weighting of LLM predictions at every time step. Our mechanism leverages the conditional information in each expert's running performance to forecast the best combination of LLMs for predicting the time series in its next step. Diverging from static (learned) Mixture of Experts (MoE) methods, MoE-F employs time-adaptive stochastic filtering techniques to combine experts. By framing the expert selection problem as a finite state-space, continuous-time Hidden Markov model (HMM), we can leverage the Wohman-Shiryaev filter. Our approach first constructs $N$ parallel filters corresponding to each of the $N$ individual LLMs. Each filter proposes its best combination of LLMs, given the information that they have access to. Subsequently, the $N$ filter outputs are aggregated to optimize a lower bound for the loss of the aggregated LLMs, which can be optimized in closed-form, thus generating our ensemble predictor. Our contributions here are: (I) the MoE-F algorithm -- deployable as a plug-and-play filtering harness, (II) theoretical optimality guarantees of the proposed filtering-based gating algorithm, and (III) empirical evaluation and ablative results using state of the art foundational and MoE LLMs on a real-world Financial Market Movement task where MoE-F attains a remarkable 17% absolute and 48.5% relative F1 measure improvement over the next best performing individual LLM expert.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge