Yannick Limmer
Uncertainty-Aware Strategies: A Model-Agnostic Framework for Robust Financial Optimization through Subsampling
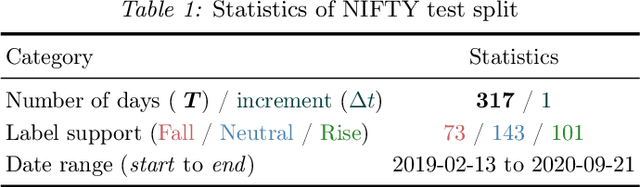
Jun 08, 2025Abstract:This paper addresses the challenge of model uncertainty in quantitative finance, where decisions in portfolio allocation, derivative pricing, and risk management rely on estimating stochastic models from limited data. In practice, the unavailability of the true probability measure forces reliance on an empirical approximation, and even small misestimations can lead to significant deviations in decision quality. Building on the framework of Klibanoff et al. (2005), we enhance the conventional objective - whether this is expected utility in an investing context or a hedging metric - by superimposing an outer "uncertainty measure", motivated by traditional monetary risk measures, on the space of models. In scenarios where a natural model distribution is lacking or Bayesian methods are impractical, we propose an ad hoc subsampling strategy, analogous to bootstrapping in statistical finance and related to mini-batch sampling in deep learning, to approximate model uncertainty. To address the quadratic memory demands of naive implementations, we also present an adapted stochastic gradient descent algorithm that enables efficient parallelization. Through analytical, simulated, and empirical studies - including multi-period, real data and high-dimensional examples - we demonstrate that uncertainty measures outperform traditional mixture of measures strategies and our model-agnostic subsampling-based approach not only enhances robustness against model risk but also achieves performance comparable to more elaborate Bayesian methods.
Filtered not Mixed: Stochastic Filtering-Based Online Gating for Mixture of Large Language Models
Jun 05, 2024
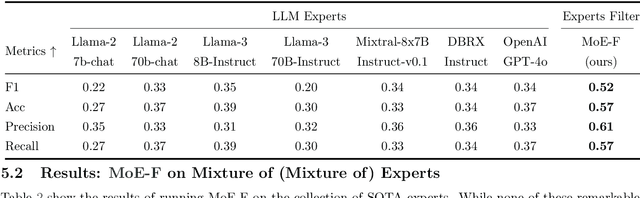
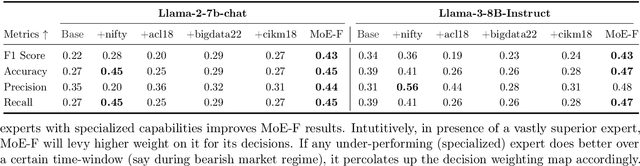
Abstract:We propose MoE-F -- a formalised mechanism for combining $N$ pre-trained expert Large Language Models (LLMs) in online time-series prediction tasks by adaptively forecasting the best weighting of LLM predictions at every time step. Our mechanism leverages the conditional information in each expert's running performance to forecast the best combination of LLMs for predicting the time series in its next step. Diverging from static (learned) Mixture of Experts (MoE) methods, MoE-F employs time-adaptive stochastic filtering techniques to combine experts. By framing the expert selection problem as a finite state-space, continuous-time Hidden Markov model (HMM), we can leverage the Wohman-Shiryaev filter. Our approach first constructs $N$ parallel filters corresponding to each of the $N$ individual LLMs. Each filter proposes its best combination of LLMs, given the information that they have access to. Subsequently, the $N$ filter outputs are aggregated to optimize a lower bound for the loss of the aggregated LLMs, which can be optimized in closed-form, thus generating our ensemble predictor. Our contributions here are: (I) the MoE-F algorithm -- deployable as a plug-and-play filtering harness, (II) theoretical optimality guarantees of the proposed filtering-based gating algorithm, and (III) empirical evaluation and ablative results using state of the art foundational and MoE LLMs on a real-world Financial Market Movement task where MoE-F attains a remarkable 17% absolute and 48.5% relative F1 measure improvement over the next best performing individual LLM expert.
Reality Only Happens Once: Single-Path Generalization Bounds for Transformers
May 26, 2024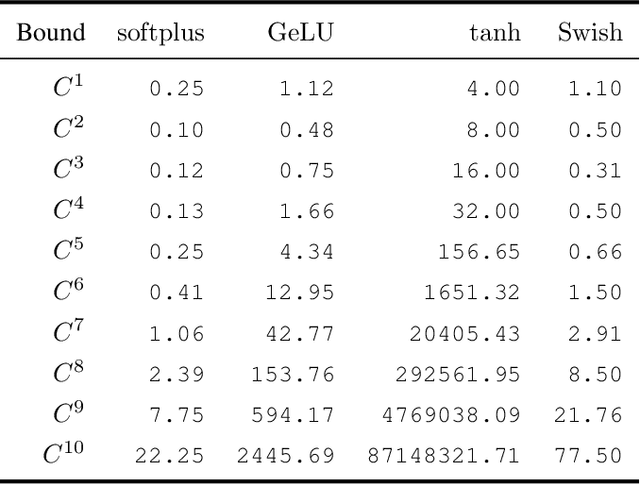
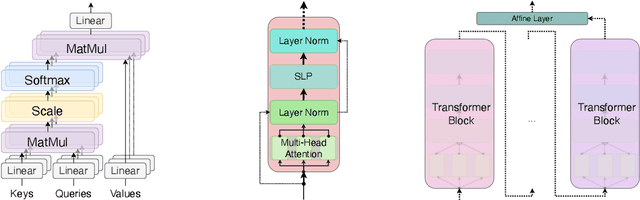

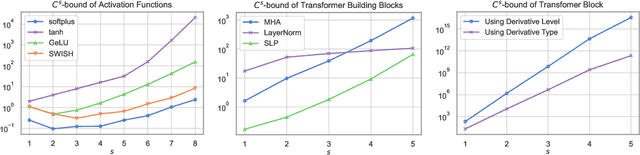
Abstract:One of the inherent challenges in deploying transformers on time series is that \emph{reality only happens once}; namely, one typically only has access to a single trajectory of the data-generating process comprised of non-i.i.d. observations. We derive non-asymptotic statistical guarantees in this setting through bounds on the \textit{generalization} of a transformer network at a future-time $t$, given that it has been trained using $N\le t$ observations from a single perturbed trajectory of a Markov process. Under the assumption that the Markov process satisfies a log-Sobolev inequality, we obtain a generalization bound which effectively converges at the rate of ${O}(1/\sqrt{N})$. Our bound depends explicitly on the activation function ($\operatorname{Swish}$, $\operatorname{GeLU}$, or $\tanh$ are considered), the number of self-attention heads, depth, width, and norm-bounds defining the transformer architecture. Our bound consists of three components: (I) The first quantifies the gap between the stationary distribution of the data-generating Markov process and its distribution at time $t$, this term converges exponentially to $0$. (II) The next term encodes the complexity of the transformer model and, given enough time, eventually converges to $0$ at the rate ${O}(\log(N)^r/\sqrt{N})$ for any $r>0$. (III) The third term guarantees that the bound holds with probability at least $1$-$\delta$, and converges at a rate of ${O}(\sqrt{\log(1/\delta)}/\sqrt{N})$.
Deep Kalman Filters Can Filter
Oct 30, 2023Abstract:Deep Kalman filters (DKFs) are a class of neural network models that generate Gaussian probability measures from sequential data. Though DKFs are inspired by the Kalman filter, they lack concrete theoretical ties to the stochastic filtering problem, thus limiting their applicability to areas where traditional model-based filters have been used, e.g.\ model calibration for bond and option prices in mathematical finance. We address this issue in the mathematical foundations of deep learning by exhibiting a class of continuous-time DKFs which can approximately implement the conditional law of a broad class of non-Markovian and conditionally Gaussian signal processes given noisy continuous-times measurements. Our approximation results hold uniformly over sufficiently regular compact subsets of paths, where the approximation error is quantified by the worst-case 2-Wasserstein distance computed uniformly over the given compact set of paths.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge