Reality Only Happens Once: Single-Path Generalization Bounds for Transformers
Paper and Code
May 26, 2024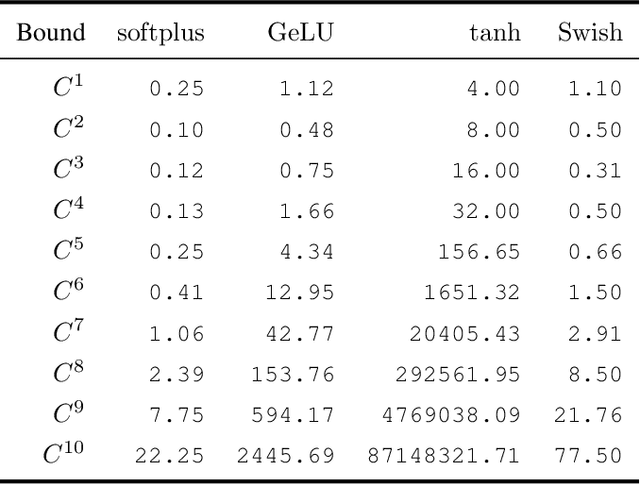
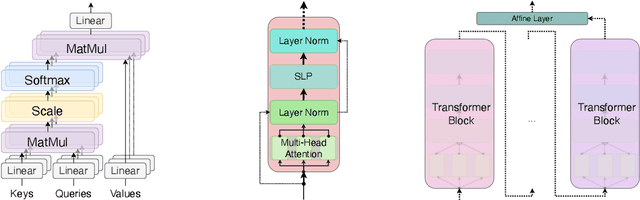

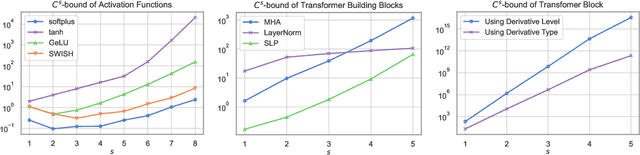
One of the inherent challenges in deploying transformers on time series is that \emph{reality only happens once}; namely, one typically only has access to a single trajectory of the data-generating process comprised of non-i.i.d. observations. We derive non-asymptotic statistical guarantees in this setting through bounds on the \textit{generalization} of a transformer network at a future-time $t$, given that it has been trained using $N\le t$ observations from a single perturbed trajectory of a Markov process. Under the assumption that the Markov process satisfies a log-Sobolev inequality, we obtain a generalization bound which effectively converges at the rate of ${O}(1/\sqrt{N})$. Our bound depends explicitly on the activation function ($\operatorname{Swish}$, $\operatorname{GeLU}$, or $\tanh$ are considered), the number of self-attention heads, depth, width, and norm-bounds defining the transformer architecture. Our bound consists of three components: (I) The first quantifies the gap between the stationary distribution of the data-generating Markov process and its distribution at time $t$, this term converges exponentially to $0$. (II) The next term encodes the complexity of the transformer model and, given enough time, eventually converges to $0$ at the rate ${O}(\log(N)^r/\sqrt{N})$ for any $r>0$. (III) The third term guarantees that the bound holds with probability at least $1$-$\delta$, and converges at a rate of ${O}(\sqrt{\log(1/\delta)}/\sqrt{N})$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge