Sparse Signature Coefficient Recovery via Kernels

Central to rough path theory is the signature transform of a path, an infinite series of tensors given by the iterated integrals of the underlying path. The signature poses an effective way to capture sequentially ordered information, thanks both to its rich analytic and algebraic properties as well as its universality when used as a basis to approximate functions on path space. Whilst a truncated version of the signature can be efficiently computed using Chen's identity, there is a lack of efficient methods for computing a sparse collection of iterated integrals contained in high levels of the signature. We address this problem by leveraging signature kernels, defined as the inner product of two signatures, and computable efficiently by means of PDE-based methods. By forming a filter in signature space with which to take kernels, one can effectively isolate specific groups of signature coefficients and, in particular, a singular coefficient at any depth of the transform. We show that such a filter can be expressed as a linear combination of suitable signature transforms and demonstrate empirically the effectiveness of our approach. To conclude, we give an example use case for sparse collections of signature coefficients based on the construction of N-step Euler schemes for sparse CDEs.

Graph Expansions of Deep Neural Networks and their Universal Scaling Limits

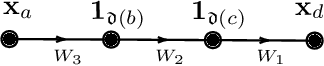
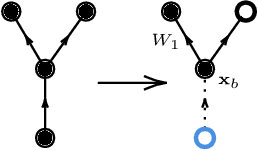
We present a unified approach to obtain scaling limits of neural networks using the genus expansion technique from random matrix theory. This approach begins with a novel expansion of neural networks which is reminiscent of Butcher series for ODEs, and is obtained through a generalisation of Fa\`a di Bruno's formula to an arbitrary number of compositions. In this expansion, the role of monomials is played by random multilinear maps indexed by directed graphs whose edges correspond to random matrices, which we call operator graphs. This expansion linearises the effect of the activation functions, allowing for the direct application of Wick's principle to compute the expectation of each of its terms. We then determine the leading contribution to each term by embedding the corresponding graphs onto surfaces, and computing their Euler characteristic. Furthermore, by developing a correspondence between analytic and graphical operations, we obtain similar graph expansions for the neural tangent kernel as well as the input-output Jacobian of the original neural network, and derive their infinite-width limits with relative ease. Notably, we find explicit formulae for the moments of the limiting singular value distribution of the Jacobian. We then show that all of these results hold for networks with more general weights, such as general matrices with i.i.d. entries satisfying moment assumptions, complex matrices and sparse matrices.

SigDiffusions: Score-Based Diffusion Models for Long Time Series via Log-Signature Embeddings

Score-based diffusion models have recently emerged as state-of-the-art generative models for a variety of data modalities. Nonetheless, it remains unclear how to adapt these models to generate long multivariate time series. Viewing a time series as the discretization of an underlying continuous process, we introduce SigDiffusion, a novel diffusion model operating on log-signature embeddings of the data. The forward and backward processes gradually perturb and denoise log-signatures preserving their algebraic structure. To recover a signal from its log-signature, we provide new closed-form inversion formulae expressing the coefficients obtained by expanding the signal in a given basis (e.g. Fourier or orthogonal polynomials) as explicit polynomial functions of the log-signature. Finally, we show that combining SigDiffusion with these inversion formulae results in highly realistic time series generation, competitive with the current state-of-the-art on various datasets of synthetic and real-world examples.

Exact Gradients for Stochastic Spiking Neural Networks Driven by Rough Signals

We introduce a mathematically rigorous framework based on rough path theory to model stochastic spiking neural networks (SSNNs) as stochastic differential equations with event discontinuities (Event SDEs) and driven by c\`adl\`ag rough paths. Our formalism is general enough to allow for potential jumps to be present both in the solution trajectories as well as in the driving noise. We then identify a set of sufficient conditions ensuring the existence of pathwise gradients of solution trajectories and event times with respect to the network's parameters and show how these gradients satisfy a recursive relation. Furthermore, we introduce a general-purpose loss function defined by means of a new class of signature kernels indexed on c\`adl\`ag rough paths and use it to train SSNNs as generative models. We provide an end-to-end autodifferentiable solver for Event SDEs and make its implementation available as part of the $\texttt{diffrax}$ library. Our framework is, to our knowledge, the first enabling gradient-based training of SSNNs with noise affecting both the spike timing and the network's dynamics.

Lecture notes on rough paths and applications to machine learning

These notes expound the recent use of the signature transform and rough path theory in data science and machine learning. We develop the core theory of the signature from first principles and then survey some recent popular applications of this approach, including signature-based kernel methods and neural rough differential equations. The notes are based on a course given by the two authors at Imperial College London.

Theoretical Foundations of Deep Selective State-Space Models

Structured state-space models (SSMs) such as S4, stemming from the seminal work of Gu et al., are gaining popularity as effective approaches for modeling sequential data. Deep SSMs demonstrate outstanding performance across a diverse set of domains, at a reduced training and inference cost compared to attention-based transformers. Recent developments show that if the linear recurrence powering SSMs allows for multiplicative interactions between inputs and hidden states (e.g. GateLoop, Mamba, GLA), then the resulting architecture can surpass in both in accuracy and efficiency attention-powered foundation models trained on text, at scales of billion parameters. In this paper, we give theoretical grounding to this recent finding using tools from Rough Path Theory: we show that when random linear recurrences are equipped with simple input-controlled transitions (selectivity mechanism), then the hidden state is provably a low-dimensional projection of a powerful mathematical object called the signature of the input -- capturing non-linear interactions between tokens at distinct timescales. Our theory not only motivates the success of modern selective state-space models such as Mamba but also provides a solid framework to understand the expressive power of future SSM variants.

Signature Kernel Conditional Independence Tests in Causal Discovery for Stochastic Processes

Inferring the causal structure underlying stochastic dynamical systems from observational data holds great promise in domains ranging from science and health to finance. Such processes can often be accurately modeled via stochastic differential equations (SDEs), which naturally imply causal relationships via "which variables enter the differential of which other variables". In this paper, we develop a kernel-based test of conditional independence (CI) on "path-space" -- solutions to SDEs -- by leveraging recent advances in signature kernels. We demonstrate strictly superior performance of our proposed CI test compared to existing approaches on path-space. Then, we develop constraint-based causal discovery algorithms for acyclic stochastic dynamical systems (allowing for loops) that leverage temporal information to recover the entire directed graph. Assuming faithfulness and a CI oracle, our algorithm is sound and complete. We empirically verify that our developed CI test in conjunction with the causal discovery algorithm reliably outperforms baselines across a range of settings.

A Neural RDE approach for continuous-time non-Markovian stochastic control problems

We propose a novel framework for solving continuous-time non-Markovian stochastic control problems by means of neural rough differential equations (Neural RDEs) introduced in Morrill et al. (2021). Non-Markovianity naturally arises in control problems due to the time delay effects in the system coefficients or the driving noises, which leads to optimal control strategies depending explicitly on the historical trajectories of the system state. By modelling the control process as the solution of a Neural RDE driven by the state process, we show that the control-state joint dynamics are governed by an uncontrolled, augmented Neural RDE, allowing for fast Monte-Carlo estimation of the value function via trajectories simulation and memory-efficient backpropagation. We provide theoretical underpinnings for the proposed algorithmic framework by demonstrating that Neural RDEs serve as universal approximators for functions of random rough paths. Exhaustive numerical experiments on non-Markovian stochastic control problems are presented, which reveal that the proposed framework is time-resolution-invariant and achieves higher accuracy and better stability in irregular sampling compared to existing RNN-based approaches.

Non-adversarial training of Neural SDEs with signature kernel scores

Neural SDEs are continuous-time generative models for sequential data. State-of-the-art performance for irregular time series generation has been previously obtained by training these models adversarially as GANs. However, as typical for GAN architectures, training is notoriously unstable, often suffers from mode collapse, and requires specialised techniques such as weight clipping and gradient penalty to mitigate these issues. In this paper, we introduce a novel class of scoring rules on pathspace based on signature kernels and use them as objective for training Neural SDEs non-adversarially. By showing strict properness of such kernel scores and consistency of the corresponding estimators, we provide existence and uniqueness guarantees for the minimiser. With this formulation, evaluating the generator-discriminator pair amounts to solving a system of linear path-dependent PDEs which allows for memory-efficient adjoint-based backpropagation. Moreover, because the proposed kernel scores are well-defined for paths with values in infinite dimensional spaces of functions, our framework can be easily extended to generate spatiotemporal data. Our procedure permits conditioning on a rich variety of market conditions and significantly outperforms alternative ways of training Neural SDEs on a variety of tasks including the simulation of rough volatility models, the conditional probabilistic forecasts of real-world forex pairs where the conditioning variable is an observed past trajectory, and the mesh-free generation of limit order book dynamics.

Neural signature kernels as infinite-width-depth-limits of controlled ResNets

Motivated by the paradigm of reservoir computing, we consider randomly initialized controlled ResNets defined as Euler-discretizations of neural controlled differential equations (Neural CDEs). We show that in the infinite-width-then-depth limit and under proper scaling, these architectures converge weakly to Gaussian processes indexed on some spaces of continuous paths and with kernels satisfying certain partial differential equations (PDEs) varying according to the choice of activation function. In the special case where the activation is the identity, we show that the equation reduces to a linear PDE and the limiting kernel agrees with the signature kernel of Salvi et al. (2021). In this setting, we also show that the width-depth limits commute. We name this new family of limiting kernels neural signature kernels. Finally, we show that in the infinite-depth regime, finite-width controlled ResNets converge in distribution to Neural CDEs with random vector fields which, depending on whether the weights are shared across layers, are either time-independent and Gaussian or behave like a matrix-valued Brownian motion.