The Exponentially Weighted Signature

The signature is a canonical representation of a multidimensional path over an interval. However, it treats all historical information uniformly, offering no intrinsic mechanism for contextualising the relevance of the past. To address this, we introduce the Exponentially Weighted Signature (EWS), generalising the Exponentially Fading Memory (EFM) signature from diagonal to general bounded linear operators. These operators enable cross-channel coupling at the level of temporal weighting together with richer memory dynamics including oscillatory, growth, and regime-dependent behaviour, while preserving the algebraic strengths of the classical signature. We show that the EWS is the unique solution to a linear controlled differential equation on the tensor algebra, and that it generalises both state-space models and the Laplace and Fourier transforms of the path. The group-like structure of the EWS enables efficient computation and makes the framework amenable to gradient-based learning, with the full semigroup action parametrised by and learned through its generator. We use this framework to empirically demonstrate the expressivity gap between the EWS and both the signature and EFM on two SDE-based regression tasks.

Structured Linear CDEs: Maximally Expressive and Parallel-in-Time Sequence Models

Structured Linear Controlled Differential Equations (SLiCEs) provide a unifying framework for sequence models with structured, input-dependent state-transition matrices that retain the maximal expressivity of dense matrices whilst being cheaper to compute. The framework encompasses existing architectures, such as input-dependent block-diagonal linear recurrent neural networks and DeltaNet's diagonal-plus-low-rank structure, as well as two novel variants based on sparsity and the Walsh--Hadamard transform. We prove that, unlike the diagonal state-transition matrices of S4 and Mamba, SLiCEs employing block-diagonal, sparse, or Walsh--Hadamard matrices match the maximal expressivity of dense matrices. Empirically, SLiCEs solve the $A_5$ state-tracking benchmark with a single layer, achieve best-in-class length generalisation on regular language tasks among parallel-in-time models, and match the state-of-the-art performance of log neural controlled differential equations on six multivariate time-series classification datasets while cutting the average time per training step by a factor of twenty.

Theoretical Foundations of Deep Selective State-Space Models

Structured state-space models (SSMs) such as S4, stemming from the seminal work of Gu et al., are gaining popularity as effective approaches for modeling sequential data. Deep SSMs demonstrate outstanding performance across a diverse set of domains, at a reduced training and inference cost compared to attention-based transformers. Recent developments show that if the linear recurrence powering SSMs allows for multiplicative interactions between inputs and hidden states (e.g. GateLoop, Mamba, GLA), then the resulting architecture can surpass in both in accuracy and efficiency attention-powered foundation models trained on text, at scales of billion parameters. In this paper, we give theoretical grounding to this recent finding using tools from Rough Path Theory: we show that when random linear recurrences are equipped with simple input-controlled transitions (selectivity mechanism), then the hidden state is provably a low-dimensional projection of a powerful mathematical object called the signature of the input -- capturing non-linear interactions between tokens at distinct timescales. Our theory not only motivates the success of modern selective state-space models such as Mamba but also provides a solid framework to understand the expressive power of future SSM variants.

Log Neural Controlled Differential Equations: The Lie Brackets Make a Difference

The vector field of a controlled differential equation (CDE) describes the relationship between a control path and the evolution of a solution path. Neural CDEs (NCDEs) treat time series data as observations from a control path, parameterise a CDE's vector field using a neural network, and use the solution path as a continuously evolving hidden state. As their formulation makes them robust to irregular sampling rates, NCDEs are a powerful approach for modelling real-world data. Building on neural rough differential equations (NRDEs), we introduce Log-NCDEs, a novel and effective method for training NCDEs. The core component of Log-NCDEs is the Log-ODE method, a tool from the study of rough paths for approximating a CDE's solution. On a range of multivariate time series classification benchmarks, Log-NCDEs are shown to achieve a higher average test set accuracy than NCDEs, NRDEs, and two state-of-the-art models, S5 and the linear recurrent unit.

Dual Bayesian ResNet: A Deep Learning Approach to Heart Murmur Detection

This study presents our team PathToMyHeart's contribution to the George B. Moody PhysioNet Challenge 2022. Two models are implemented. The first model is a Dual Bayesian ResNet (DBRes), where each patient's recording is segmented into overlapping log mel spectrograms. These undergo two binary classifications: present versus unknown or absent, and unknown versus present or absent. The classifications are aggregated to give a patient's final classification. The second model is the output of DBRes integrated with demographic data and signal features using XGBoost.DBRes achieved our best weighted accuracy of $0.771$ on the hidden test set for murmur classification, which placed us fourth for the murmur task. (On the clinical outcome task, which we neglected, we scored 17th with costs of $12637$.) On our held-out subset of the training set, integrating the demographic data and signal features improved DBRes's accuracy from $0.762$ to $0.820$. However, this decreased DBRes's weighted accuracy from $0.780$ to $0.749$. Our results demonstrate that log mel spectrograms are an effective representation of heart sound recordings, Bayesian networks provide strong supervised classification performance, and treating the ternary classification as two binary classifications increases performance on the weighted accuracy.

Learning Dynamic Graph Embeddings with Neural Controlled Differential Equations

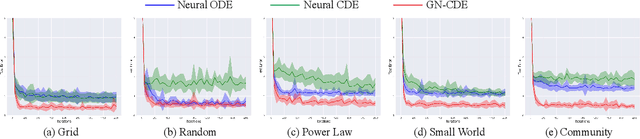
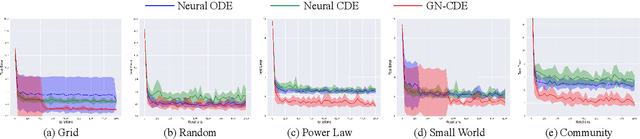
This paper focuses on representation learning for dynamic graphs with temporal interactions. A fundamental issue is that both the graph structure and the nodes own their own dynamics, and their blending induces intractable complexity in the temporal evolution over graphs. Drawing inspiration from the recent process of physical dynamic models in deep neural networks, we propose Graph Neural Controlled Differential Equation (GN-CDE) model, a generic differential model for dynamic graphs that characterise the continuously dynamic evolution of node embedding trajectories with a neural network parameterised vector field and the derivatives of interactions w.r.t. time. Our framework exhibits several desirable characteristics, including the ability to express dynamics on evolving graphs without integration by segments, the capability to calibrate trajectories with subsequent data, and robustness to missing observations. Empirical evaluation on a range of dynamic graph representation learning tasks demonstrates the superiority of our proposed approach compared to the baselines.