Antonio Orvieto
ETH Zurich
Scaling Behavior of Discrete Diffusion Language Models
Dec 11, 2025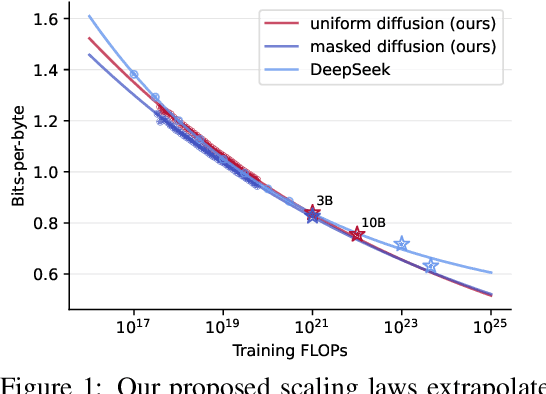
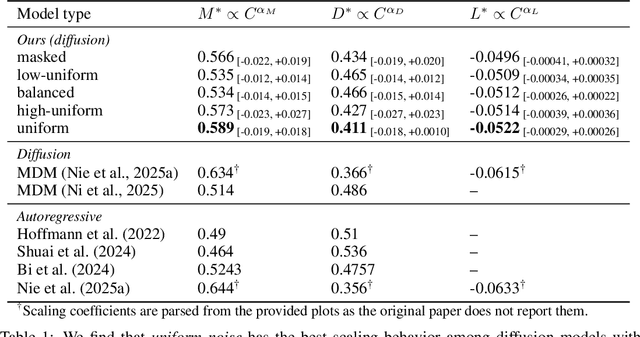
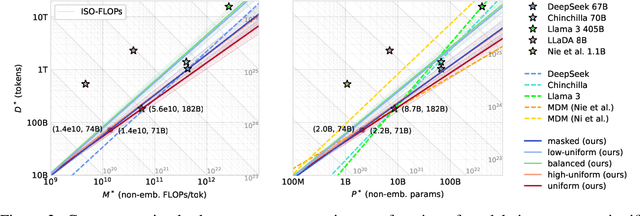
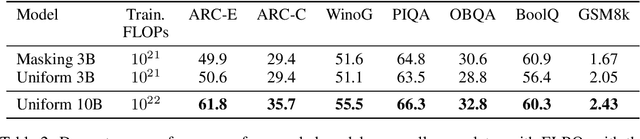
Abstract:Modern LLM pre-training consumes vast amounts of compute and training data, making the scaling behavior, or scaling laws, of different models a key distinguishing factor. Discrete diffusion language models (DLMs) have been proposed as an alternative to autoregressive language models (ALMs). However, their scaling behavior has not yet been fully explored, with prior work suggesting that they require more data and compute to match the performance of ALMs. We study the scaling behavior of DLMs on different noise types by smoothly interpolating between masked and uniform diffusion while paying close attention to crucial hyperparameters such as batch size and learning rate. Our experiments reveal that the scaling behavior of DLMs strongly depends on the noise type and is considerably different from ALMs. While all noise types converge to similar loss values in compute-bound scaling, we find that uniform diffusion requires more parameters and less data for compute-efficient training compared to masked diffusion, making them a promising candidate in data-bound settings. We scale our uniform diffusion model up to 10B parameters trained for $10^{22}$ FLOPs, confirming the predicted scaling behavior and making it the largest publicly known uniform diffusion model to date.
Design Principles for Sequence Models via Coefficient Dynamics
Oct 10, 2025



Abstract:Deep sequence models, ranging from Transformers and State Space Models (SSMs) to more recent approaches such as gated linear RNNs, fundamentally compute outputs as linear combinations of past value vectors. To draw insights and systematically compare such architectures, we develop a unified framework that makes this output operation explicit, by casting the linear combination coefficients as the outputs of autonomous linear dynamical systems driven by impulse inputs. This viewpoint, in spirit substantially different from approaches focusing on connecting linear RNNs with linear attention, reveals a common mathematical theme across diverse architectures and crucially captures softmax attention, on top of RNNs, SSMs, and related models. In contrast to new model proposals that are commonly evaluated on benchmarks, we derive design principles linking architectural choices to model properties. Thereby identifying tradeoffs between expressivity and efficient implementation, geometric constraints on input selectivity, and stability conditions for numerically stable training and information retention. By connecting several insights and observations from recent literature, the framework both explains empirical successes of recent designs and provides guiding principles for systematically designing new sequence model architectures.
How does the optimizer implicitly bias the model merging loss landscape?
Oct 06, 2025Abstract:Model merging methods combine models with different capabilities into a single one while maintaining the same inference cost. Two popular approaches are linear interpolation, which linearly interpolates between model weights, and task arithmetic, which combines task vectors obtained by the difference between finetuned and base models. While useful in practice, what properties make merging effective are poorly understood. This paper explores how the optimization process affects the loss landscape geometry and its impact on merging success. We show that a single quantity -- the effective noise scale -- unifies the impact of optimizer and data choices on model merging. Across architectures and datasets, the effectiveness of merging success is a non-monotonic function of effective noise, with a distinct optimum. Decomposing this quantity, we find that larger learning rates, stronger weight decay, smaller batch sizes, and data augmentation all independently modulate the effective noise scale, exhibiting the same qualitative trend. Unlike prior work that connects optimizer noise to the flatness or generalization of individual minima, we show that it also affects the global loss landscape, predicting when independently trained solutions can be merged. Our findings broaden the understanding of how optimization shapes the loss landscape geometry and its downstream consequences for model merging, suggesting the possibility of further manipulating the training dynamics to improve merging effectiveness.
When recalling in-context, Transformers are not SSMs
Aug 26, 2025Abstract:Despite the advantageous subquadratic complexity of modern recurrent deep learning models -- such as state-space models (SSMs) -- recent studies have highlighted their potential shortcomings compared to transformers on reasoning and memorization tasks. In this paper, we dive deeper into one of such benchmarks: associative recall (AR), which has been shown to correlate well with language modeling performance, and inspect in detail the effects of scaling and optimization issues in recently proposed token mixing strategies. We first demonstrate that, unlike standard transformers, the choice of learning rate plays a critical role in the performance of modern recurrent models: an issue that can severely affect reported performance in previous works and suggests further research is needed to stabilize training. Next, we show that recurrent and attention-based models exhibit contrasting benefits when scaling in width as opposed to depth, with attention being notably unable to solve AR when limited to a single layer. We then further inspect 1-layer transformers, revealing that despite their poor performance, their training dynamics surprisingly resemble the formation of induction heads, a phenomenon previously observed only in their 2-layer counterparts. Finally, through architectural ablations, we study how components affects Transformer and Mamba's performance and optimization stability.
Enhancing Optimizer Stability: Momentum Adaptation of The NGN Step-size
Aug 20, 2025Abstract:Modern optimization algorithms that incorporate momentum and adaptive step-size offer improved performance in numerous challenging deep learning tasks. However, their effectiveness is often highly sensitive to the choice of hyperparameters, especially the step-size. Tuning these parameters is often difficult, resource-intensive, and time-consuming. Therefore, recent efforts have been directed toward enhancing the stability of optimizers across a wide range of hyperparameter choices [Schaipp et al., 2024]. In this paper, we introduce an algorithm that matches the performance of state-of-the-art optimizers while improving stability to the choice of the step-size hyperparameter through a novel adaptation of the NGN step-size method [Orvieto and Xiao, 2024]. Specifically, we propose a momentum-based version (NGN-M) that attains the standard convergence rate of $\mathcal{O}(1/\sqrt{K})$ under less restrictive assumptions, without the need for interpolation condition or assumptions of bounded stochastic gradients or iterates, in contrast to previous approaches. Additionally, we empirically demonstrate that the combination of the NGN step-size with momentum results in enhanced robustness to the choice of the step-size hyperparameter while delivering performance that is comparable to or surpasses other state-of-the-art optimizers.
GitChameleon: Evaluating AI Code Generation Against Python Library Version Incompatibilities
Jul 16, 2025
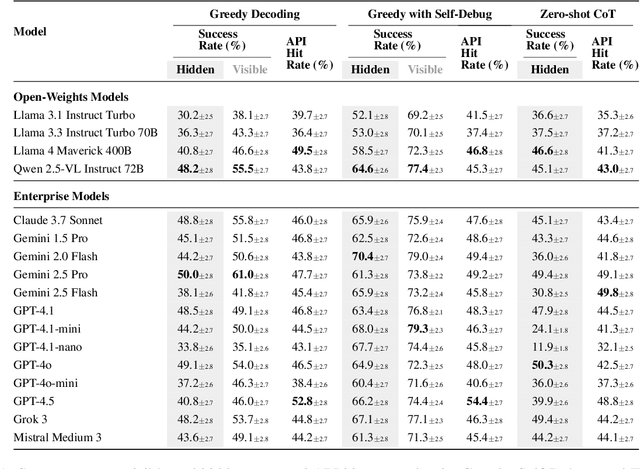
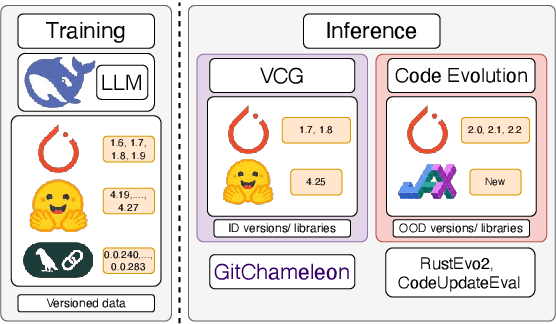
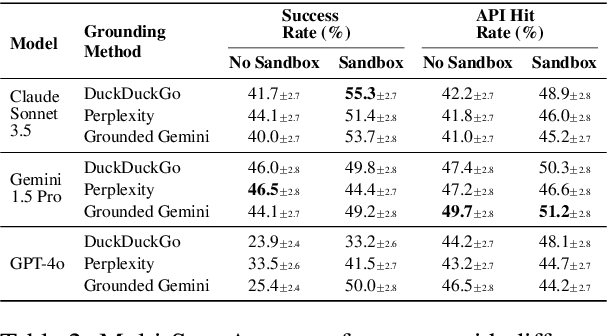
Abstract:The rapid evolution of software libraries poses a considerable hurdle for code generation, necessitating continuous adaptation to frequent version updates while preserving backward compatibility. While existing code evolution benchmarks provide valuable insights, they typically lack execution-based evaluation for generating code compliant with specific library versions. To address this, we introduce GitChameleon, a novel, meticulously curated dataset comprising 328 Python code completion problems, each conditioned on specific library versions and accompanied by executable unit tests. GitChameleon rigorously evaluates the capacity of contemporary large language models (LLMs), LLM-powered agents, code assistants, and RAG systems to perform version-conditioned code generation that demonstrates functional accuracy through execution. Our extensive evaluations indicate that state-of-the-art systems encounter significant challenges with this task; enterprise models achieving baseline success rates in the 48-51\% range, underscoring the intricacy of the problem. By offering an execution-based benchmark emphasizing the dynamic nature of code libraries, GitChameleon enables a clearer understanding of this challenge and helps guide the development of more adaptable and dependable AI code generation methods. We make the dataset and evaluation code publicly available at https://github.com/mrcabbage972/GitChameleonBenchmark.
Is your batch size the problem? Revisiting the Adam-SGD gap in language modeling
Jun 14, 2025Abstract:Adam is known to perform significantly better than Stochastic Gradient Descent (SGD) in language models, a phenomenon for which a number of explanations have been proposed. In this work, we revisit this "optimizer gap" through a series of comprehensively tuned baseline training runs for language modeling with Transformers. We exhaustively study how momentum, gradient clipping, and batch size affect the gap between SGD and Adam. Our empirical findings show that SGD with momentum can actually perform similarly to Adam in small-batch settings, if tuned correctly. We revisit existing explanations for Adam's advantage, including heavy-tailed class imbalance, directional sharpness, and Hessian heterogeneity, which struggle to directly explain this phenomenon. Towards bridging this gap in our understanding, by analyzing our Transformer training runs and simple quadratic settings inspired by the literature, we provide new insights, driven by stochastic differential equation models, into the role of batch size on the training dynamics.
In Search of Adam's Secret Sauce
May 27, 2025Abstract:Understanding the remarkable efficacy of Adam when training transformer-based language models has become a central research topic within the optimization community. To gain deeper insights, several simplifications of Adam have been proposed, such as the signed gradient and signed momentum methods. In this work, we conduct an extensive empirical study - training over 1,300 language models across different data configurations and scales - comparing Adam to several known simplified variants. We find that signed momentum methods are faster than SGD, but consistently underperform relative to Adam, even after careful tuning of momentum, clipping setting and learning rates. However, our analysis reveals a compelling option that preserves near-optimal performance while allowing for new insightful reformulations: constraining the Adam momentum parameters to be equal. Beyond robust performance, this choice affords new theoretical insights, highlights the "secret sauce" on top of signed momentum, and grants a precise statistical interpretation: we show that Adam in this setting implements a natural online algorithm for estimating the mean and variance of gradients-one that arises from a mean-field Gaussian variational inference perspective.
Can you Finetune your Binoculars? Embedding Text Watermarks into the Weights of Large Language Models
Apr 08, 2025



Abstract:The indistinguishability of AI-generated content from human text raises challenges in transparency and accountability. While several methods exist to watermark models behind APIs, embedding watermark strategies directly into model weights that are later reflected in the outputs of the model is challenging. In this study we propose a strategy to finetune a pair of low-rank adapters of a model, one serving as the text-generating model, and the other as the detector, so that a subtle watermark is embedded into the text generated by the first model and simultaneously optimized for detectability by the second. In this way, the watermarking strategy is fully learned end-to-end. This process imposes an optimization challenge, as balancing watermark robustness, naturalness, and task performance requires trade-offs. We discuss strategies on how to optimize this min-max objective and present results showing the effect of this modification to instruction finetuning.
Fixed-Point RNNs: From Diagonal to Dense in a Few Iterations
Mar 13, 2025



Abstract:Linear recurrent neural networks (RNNs) and state-space models (SSMs) such as Mamba have become promising alternatives to softmax-attention as sequence mixing layers in Transformer architectures. Current models, however, do not exhibit the full state-tracking expressivity of RNNs because they rely on channel-wise (i.e. diagonal) sequence mixing. In this paper, we propose to compute a dense linear RNN as the fixed-point of a parallelizable diagonal linear RNN in a single layer. We explore mechanisms to improve its memory and state-tracking abilities in practice, and achieve state-of-the-art results on the commonly used toy tasks $A_5$, $S_5$, copying, and modular arithmetics. We hope our results will open new avenues to more expressive and efficient sequence mixers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge