Adaptive Methods through the Lens of SDEs: Theoretical Insights on the Role of Noise

Despite the vast empirical evidence supporting the efficacy of adaptive optimization methods in deep learning, their theoretical understanding is far from complete. This work introduces novel SDEs for commonly used adaptive optimizers: SignSGD, RMSprop(W), and Adam(W). These SDEs offer a quantitatively accurate description of these optimizers and help illuminate an intricate relationship between adaptivity, gradient noise, and curvature. Our novel analysis of SignSGD highlights a noteworthy and precise contrast to SGD in terms of convergence speed, stationary distribution, and robustness to heavy-tail noise. We extend this analysis to AdamW and RMSpropW, for which we observe that the role of noise is much more complex. Crucially, we support our theoretical analysis with experimental evidence by verifying our insights: this includes numerically integrating our SDEs using Euler-Maruyama discretization on various neural network architectures such as MLPs, CNNs, ResNets, and Transformers. Our SDEs accurately track the behavior of the respective optimizers, especially when compared to previous SDEs derived for Adam and RMSprop. We believe our approach can provide valuable insights into best training practices and novel scaling rules.

SDEs for Minimax Optimization

Minimax optimization problems have attracted a lot of attention over the past few years, with applications ranging from economics to machine learning. While advanced optimization methods exist for such problems, characterizing their dynamics in stochastic scenarios remains notably challenging. In this paper, we pioneer the use of stochastic differential equations (SDEs) to analyze and compare Minimax optimizers. Our SDE models for Stochastic Gradient Descent-Ascent, Stochastic Extragradient, and Stochastic Hamiltonian Gradient Descent are provable approximations of their algorithmic counterparts, clearly showcasing the interplay between hyperparameters, implicit regularization, and implicit curvature-induced noise. This perspective also allows for a unified and simplified analysis strategy based on the principles of It\^o calculus. Finally, our approach facilitates the derivation of convergence conditions and closed-form solutions for the dynamics in simplified settings, unveiling further insights into the behavior of different optimizers.

An SDE for Modeling SAM: Theory and Insights

We study the SAM (Sharpness-Aware Minimization) optimizer which has recently attracted a lot of interest due to its increased performance over more classical variants of stochastic gradient descent. Our main contribution is the derivation of continuous-time models (in the form of SDEs) for SAM and its unnormalized variant USAM, both for the full-batch and mini-batch settings. We demonstrate that these SDEs are rigorous approximations of the real discrete-time algorithms (in a weak sense, scaling linearly with the step size). Using these models, we then offer an explanation of why SAM prefers flat minima over sharp ones - by showing that it minimizes an implicitly regularized loss with a Hessian-dependent noise structure. Finally, we prove that perhaps unexpectedly SAM is attracted to saddle points under some realistic conditions. Our theoretical results are supported by detailed experiments.

Randomized Signature Layers for Signal Extraction in Time Series Data

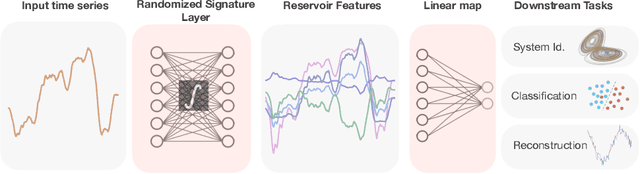
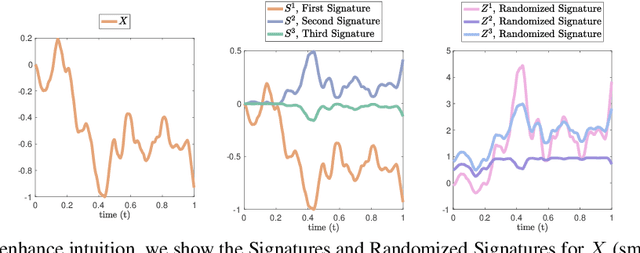
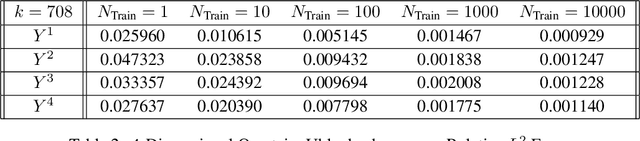
Time series analysis is a widespread task in Natural Sciences, Social Sciences, and Engineering. A fundamental problem is finding an expressive yet efficient-to-compute representation of the input time series to use as a starting point to perform arbitrary downstream tasks. In this paper, we build upon recent works that use the Signature of a path as a feature map and investigate a computationally efficient technique to approximate these features based on linear random projections. We present several theoretical results to justify our approach and empirically validate that our random projections can effectively retrieve the underlying Signature of a path. We show the surprising performance of the proposed random features on several tasks, including (1) mapping the controls of stochastic differential equations to the corresponding solutions and (2) using the Randomized Signatures as time series representation for classification tasks. When compared to corresponding truncated Signature approaches, our Randomizes Signatures are more computationally efficient in high dimensions and often lead to better accuracy and faster training. Besides providing a new tool to extract Signatures and further validating the high level of expressiveness of such features, we believe our results provide interesting conceptual links between several existing research areas, suggesting new intriguing directions for future investigations.