Bilinear Sequence Regression: A Model for Learning from Long Sequences of High-dimensional Tokens

Current progress in artificial intelligence is centered around so-called large language models that consist of neural networks processing long sequences of high-dimensional vectors called tokens. Statistical physics provides powerful tools to study the functioning of learning with neural networks and has played a recognized role in the development of modern machine learning. The statistical physics approach relies on simplified and analytically tractable models of data. However, simple tractable models for long sequences of high-dimensional tokens are largely underexplored. Inspired by the crucial role models such as the single-layer teacher-student perceptron (aka generalized linear regression) played in the theory of fully connected neural networks, in this paper, we introduce and study the bilinear sequence regression (BSR) as one of the most basic models for sequences of tokens. We note that modern architectures naturally subsume the BSR model due to the skip connections. Building on recent methodological progress, we compute the Bayes-optimal generalization error for the model in the limit of long sequences of high-dimensional tokens, and provide a message-passing algorithm that matches this performance. We quantify the improvement that optimal learning brings with respect to vectorizing the sequence of tokens and learning via simple linear regression. We also unveil surprising properties of the gradient descent algorithms in the BSR model.

Understanding Counting in Small Transformers: The Interplay between Attention and Feed-Forward Layers

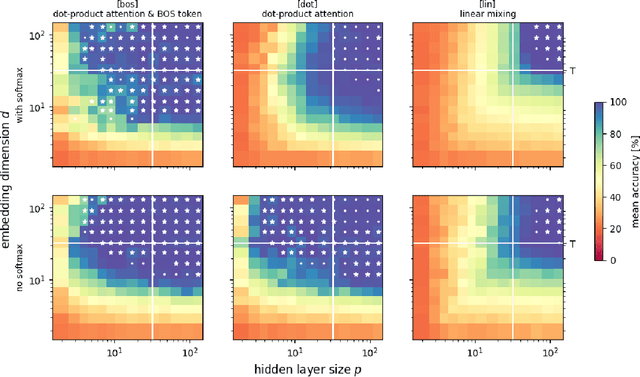
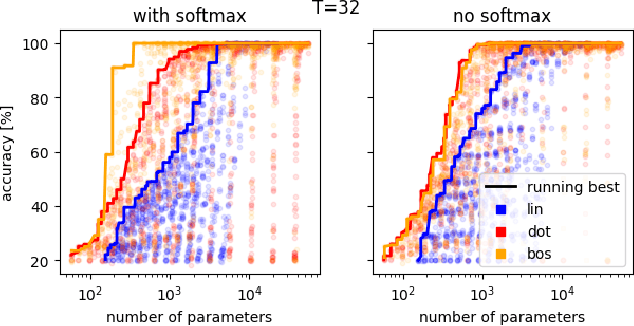
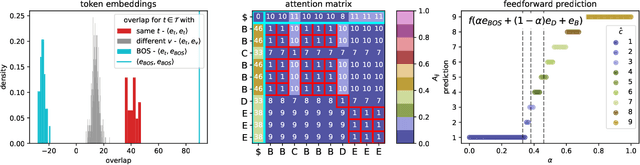
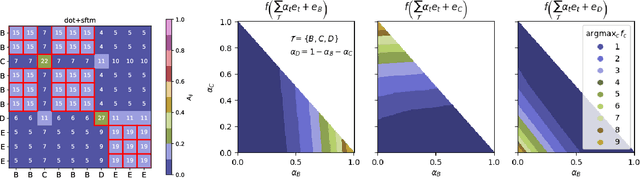
We provide a comprehensive analysis of simple transformer models trained on the histogram task, where the goal is to count the occurrences of each item in the input sequence from a fixed alphabet. Despite its apparent simplicity, this task exhibits a rich phenomenology that allows us to characterize how different architectural components contribute towards the emergence of distinct algorithmic solutions. In particular, we showcase the existence of two qualitatively different mechanisms that implement a solution, relation- and inventory-based counting. Which solution a model can implement depends non-trivially on the precise choice of the attention mechanism, activation function, memorization capacity and the presence of a beginning-of-sequence token. By introspecting learned models on the counting task, we find evidence for the formation of both mechanisms. From a broader perspective, our analysis offers a framework to understand how the interaction of different architectural components of transformer models shapes diverse algorithmic solutions and approximations.

Harnessing Synthetic Datasets: The Role of Shape Bias in Deep Neural Network Generalization

Recent advancements in deep learning have been primarily driven by the use of large models trained on increasingly vast datasets. While neural scaling laws have emerged to predict network performance given a specific level of computational resources, the growing demand for expansive datasets raises concerns. To address this, a new research direction has emerged, focusing on the creation of synthetic data as a substitute. In this study, we investigate how neural networks exhibit shape bias during training on synthetic datasets, serving as an indicator of the synthetic data quality. Specifically, our findings indicate three key points: (1) Shape bias varies across network architectures and types of supervision, casting doubt on its reliability as a predictor for generalization and its ability to explain differences in model recognition compared to human capabilities. (2) Relying solely on shape bias to estimate generalization is unreliable, as it is entangled with diversity and naturalism. (3) We propose a novel interpretation of shape bias as a tool for estimating the diversity of samples within a dataset. Our research aims to clarify the implications of using synthetic data and its associated shape bias in deep learning, addressing concerns regarding generalization and dataset quality.

Gemtelligence: Accelerating Gemstone classification with Deep Learning

The value of luxury goods, particularly investment-grade gemstones, is greatly influenced by their origin and authenticity, sometimes resulting in differences worth millions of dollars. Traditionally, human experts have determined the origin and detected treatments on gemstones through visual inspections and a range of analytical methods. However, the interpretation of the data can be subjective and time-consuming, resulting in inconsistencies. In this study, we propose Gemtelligence, a novel approach based on deep learning that enables accurate and consistent origin determination and treatment detection. Gemtelligence comprises convolutional and attention-based neural networks that process heterogeneous data types collected by multiple instruments. Notably, the algorithm demonstrated comparable predictive performance to expensive laser-ablation inductively-coupled-plasma mass-spectrometry (ICP-MS) analysis and visual examination by human experts, despite using input data from relatively inexpensive analytical methods. Our innovative methodology represents a major breakthrough in the field of gemstone analysis by significantly improving the automation and robustness of the entire analytical process pipeline.

Dynamic Context Pruning for Efficient and Interpretable Autoregressive Transformers

Autoregressive Transformers adopted in Large Language Models (LLMs) are hard to scale to long sequences. Despite several works trying to reduce their computational cost, most of LLMs still adopt attention layers between all pairs of tokens in the sequence, thus incurring a quadratic cost. In this study, we present a novel approach that dynamically prunes contextual information while preserving the model's expressiveness, resulting in reduced memory and computational requirements during inference. Our method employs a learnable mechanism that determines which uninformative tokens can be dropped from the context at any point across the generation process. By doing so, our approach not only addresses performance concerns but also enhances interpretability, providing valuable insight into the model's decision-making process. Our technique can be applied to existing pre-trained models through a straightforward fine-tuning process, and the pruning strength can be specified by a sparsity parameter. Notably, our empirical findings demonstrate that we can effectively prune up to 80\% of the context without significant performance degradation on downstream tasks, offering a valuable tool for mitigating inference costs. Our reference implementation achieves up to $2\times$ increase in inference throughput and even greater memory savings.

Uncertainty Quantification in Machine Learning for Engineering Design and Health Prognostics: A Tutorial

On top of machine learning models, uncertainty quantification (UQ) functions as an essential layer of safety assurance that could lead to more principled decision making by enabling sound risk assessment and management. The safety and reliability improvement of ML models empowered by UQ has the potential to significantly facilitate the broad adoption of ML solutions in high-stakes decision settings, such as healthcare, manufacturing, and aviation, to name a few. In this tutorial, we aim to provide a holistic lens on emerging UQ methods for ML models with a particular focus on neural networks and the applications of these UQ methods in tackling engineering design as well as prognostics and health management problems. Toward this goal, we start with a comprehensive classification of uncertainty types, sources, and causes pertaining to UQ of ML models. Next, we provide a tutorial-style description of several state-of-the-art UQ methods: Gaussian process regression, Bayesian neural network, neural network ensemble, and deterministic UQ methods focusing on spectral-normalized neural Gaussian process. Established upon the mathematical formulations, we subsequently examine the soundness of these UQ methods quantitatively and qualitatively (by a toy regression example) to examine their strengths and shortcomings from different dimensions. Then, we review quantitative metrics commonly used to assess the quality of predictive uncertainty in classification and regression problems. Afterward, we discuss the increasingly important role of UQ of ML models in solving challenging problems in engineering design and health prognostics. Two case studies with source codes available on GitHub are used to demonstrate these UQ methods and compare their performance in the life prediction of lithium-ion batteries at the early stage and the remaining useful life prediction of turbofan engines.

Controllable Neural Symbolic Regression

In symbolic regression, the goal is to find an analytical expression that accurately fits experimental data with the minimal use of mathematical symbols such as operators, variables, and constants. However, the combinatorial space of possible expressions can make it challenging for traditional evolutionary algorithms to find the correct expression in a reasonable amount of time. To address this issue, Neural Symbolic Regression (NSR) algorithms have been developed that can quickly identify patterns in the data and generate analytical expressions. However, these methods, in their current form, lack the capability to incorporate user-defined prior knowledge, which is often required in natural sciences and engineering fields. To overcome this limitation, we propose a novel neural symbolic regression method, named Neural Symbolic Regression with Hypothesis (NSRwH) that enables the explicit incorporation of assumptions about the expected structure of the ground-truth expression into the prediction process. Our experiments demonstrate that the proposed conditioned deep learning model outperforms its unconditioned counterparts in terms of accuracy while also providing control over the predicted expression structure.

An SDE for Modeling SAM: Theory and Insights

We study the SAM (Sharpness-Aware Minimization) optimizer which has recently attracted a lot of interest due to its increased performance over more classical variants of stochastic gradient descent. Our main contribution is the derivation of continuous-time models (in the form of SDEs) for SAM and its unnormalized variant USAM, both for the full-batch and mini-batch settings. We demonstrate that these SDEs are rigorous approximations of the real discrete-time algorithms (in a weak sense, scaling linearly with the step size). Using these models, we then offer an explanation of why SAM prefers flat minima over sharp ones - by showing that it minimizes an implicitly regularized loss with a Hessian-dependent noise structure. Finally, we prove that perhaps unexpectedly SAM is attracted to saddle points under some realistic conditions. Our theoretical results are supported by detailed experiments.

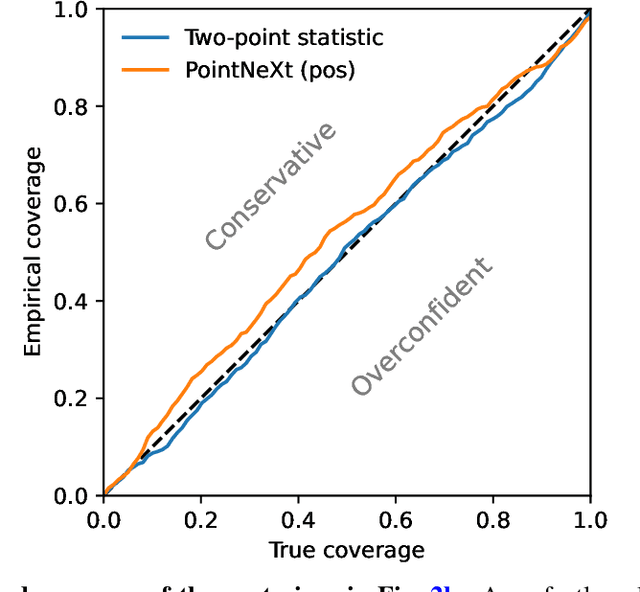
Cosmology from Galaxy Redshift Surveys with PointNet

In recent years, deep learning approaches have achieved state-of-the-art results in the analysis of point cloud data. In cosmology, galaxy redshift surveys resemble such a permutation invariant collection of positions in space. These surveys have so far mostly been analysed with two-point statistics, such as power spectra and correlation functions. The usage of these summary statistics is best justified on large scales, where the density field is linear and Gaussian. However, in light of the increased precision expected from upcoming surveys, the analysis of -- intrinsically non-Gaussian -- small angular separations represents an appealing avenue to better constrain cosmological parameters. In this work, we aim to improve upon two-point statistics by employing a \textit{PointNet}-like neural network to regress the values of the cosmological parameters directly from point cloud data. Our implementation of PointNets can analyse inputs of $\mathcal{O}(10^4) - \mathcal{O}(10^5)$ galaxies at a time, which improves upon earlier work for this application by roughly two orders of magnitude. Additionally, we demonstrate the ability to analyse galaxy redshift survey data on the lightcone, as opposed to previously static simulation boxes at a given fixed redshift.

Signal Propagation in Transformers: Theoretical Perspectives and the Role of Rank Collapse

Transformers have achieved remarkable success in several domains, ranging from natural language processing to computer vision. Nevertheless, it has been recently shown that stacking self-attention layers - the distinctive architectural component of Transformers - can result in rank collapse of the tokens' representations at initialization. The question of if and how rank collapse affects training is still largely unanswered, and its investigation is necessary for a more comprehensive understanding of this architecture. In this work, we shed new light on the causes and the effects of this phenomenon. First, we show that rank collapse of the tokens' representations hinders training by causing the gradients of the queries and keys to vanish at initialization. Furthermore, we provide a thorough description of the origin of rank collapse and discuss how to prevent it via an appropriate depth-dependent scaling of the residual branches. Finally, our analysis unveils that specific architectural hyperparameters affect the gradients of queries and values differently, leading to disproportionate gradient norms. This suggests an explanation for the widespread use of adaptive methods for Transformers' optimization.