Dataset distillation for memorized data: Soft labels can leak held-out teacher knowledge

Dataset distillation aims to compress training data into fewer examples via a teacher, from which a student can learn effectively. While its success is often attributed to structure in the data, modern neural networks also memorize specific facts, but if and how such memorized information is can transferred in distillation settings remains less understood. In this work, we show that students trained on soft labels from teachers can achieve non-trivial accuracy on held-out memorized data they never directly observed. This effect persists on structured data when the teacher has not generalized.To analyze it in isolation, we consider finite random i.i.d. datasets where generalization is a priori impossible and a successful teacher fit implies pure memorization. Still, students can learn non-trivial information about the held-out data, in some cases up to perfect accuracy. In those settings, enough soft labels are available to recover the teacher functionally - the student matches the teacher's predictions on all possible inputs, including the held-out memorized data. We show that these phenomena strongly depend on the temperature with which the logits are smoothed, but persist across varying network capacities, architectures and dataset compositions.

On the existence of consistent adversarial attacks in high-dimensional linear classification

What fundamentally distinguishes an adversarial attack from a misclassification due to limited model expressivity or finite data? In this work, we investigate this question in the setting of high-dimensional binary classification, where statistical effects due to limited data availability play a central role. We introduce a new error metric that precisely capture this distinction, quantifying model vulnerability to consistent adversarial attacks -- perturbations that preserve the ground-truth labels. Our main technical contribution is an exact and rigorous asymptotic characterization of these metrics in both well-specified models and latent space models, revealing different vulnerability patterns compared to standard robust error measures. The theoretical results demonstrate that as models become more overparameterized, their vulnerability to label-preserving perturbations grows, offering theoretical insight into the mechanisms underlying model sensitivity to adversarial attacks.

Learning with Restricted Boltzmann Machines: Asymptotics of AMP and GD in High Dimensions

The Restricted Boltzmann Machine (RBM) is one of the simplest generative neural networks capable of learning input distributions. Despite its simplicity, the analysis of its performance in learning from the training data is only well understood in cases that essentially reduce to singular value decomposition of the data. Here, we consider the limit of a large dimension of the input space and a constant number of hidden units. In this limit, we simplify the standard RBM training objective into a form that is equivalent to the multi-index model with non-separable regularization. This opens a path to analyze training of the RBM using methods that are established for multi-index models, such as Approximate Message Passing (AMP) and its state evolution, and the analysis of Gradient Descent (GD) via the dynamical mean-field theory. We then give rigorous asymptotics of the training dynamics of RBM on data generated by the spiked covariance model as a prototype of a structure suitable for unsupervised learning. We show in particular that RBM reaches the optimal computational weak recovery threshold, aligning with the BBP transition, in the spiked covariance model.

The Nuclear Route: Sharp Asymptotics of ERM in Overparameterized Quadratic Networks

We study the high-dimensional asymptotics of empirical risk minimization (ERM) in over-parametrized two-layer neural networks with quadratic activations trained on synthetic data. We derive sharp asymptotics for both training and test errors by mapping the $\ell_2$-regularized learning problem to a convex matrix sensing task with nuclear norm penalization. This reveals that capacity control in such networks emerges from a low-rank structure in the learned feature maps. Our results characterize the global minima of the loss and yield precise generalization thresholds, showing how the width of the target function governs learnability. This analysis bridges and extends ideas from spin-glass methods, matrix factorization, and convex optimization and emphasizes the deep link between low-rank matrix sensing and learning in quadratic neural networks.

Fundamental Limits of Matrix Sensing: Exact Asymptotics, Universality, and Applications

In the matrix sensing problem, one wishes to reconstruct a matrix from (possibly noisy) observations of its linear projections along given directions. We consider this model in the high-dimensional limit: while previous works on this model primarily focused on the recovery of low-rank matrices, we consider in this work more general classes of structured signal matrices with potentially large rank, e.g. a product of two matrices of sizes proportional to the dimension. We provide rigorous asymptotic equations characterizing the Bayes-optimal learning performance from a number of samples which is proportional to the number of entries in the matrix. Our proof is composed of three key ingredients: $(i)$ we prove universality properties to handle structured sensing matrices, related to the ''Gaussian equivalence'' phenomenon in statistical learning, $(ii)$ we provide a sharp characterization of Bayes-optimal learning in generalized linear models with Gaussian data and structured matrix priors, generalizing previously studied settings, and $(iii)$ we leverage previous works on the problem of matrix denoising. The generality of our results allow for a variety of applications: notably, we mathematically establish predictions obtained via non-rigorous methods from statistical physics in [ETB+24] regarding Bilinear Sequence Regression, a benchmark model for learning from sequences of tokens, and in [MTM+24] on Bayes-optimal learning in neural networks with quadratic activation function, and width proportional to the dimension.

The Computational Advantage of Depth: Learning High-Dimensional Hierarchical Functions with Gradient Descent

Understanding the advantages of deep neural networks trained by gradient descent (GD) compared to shallow models remains an open theoretical challenge. While the study of multi-index models with Gaussian data in high dimensions has provided analytical insights into the benefits of GD-trained neural networks over kernels, the role of depth in improving sample complexity and generalization in GD-trained networks remains poorly understood. In this paper, we introduce a class of target functions (single and multi-index Gaussian hierarchical targets) that incorporate a hierarchy of latent subspace dimensionalities. This framework enables us to analytically study the learning dynamics and generalization performance of deep networks compared to shallow ones in the high-dimensional limit. Specifically, our main theorem shows that feature learning with GD reduces the effective dimensionality, transforming a high-dimensional problem into a sequence of lower-dimensional ones. This enables learning the target function with drastically less samples than with shallow networks. While the results are proven in a controlled training setting, we also discuss more common training procedures and argue that they learn through the same mechanisms. These findings open the way to further quantitative studies of the crucial role of depth in learning hierarchical structures with deep networks.

Fundamental limits of learning in sequence multi-index models and deep attention networks: High-dimensional asymptotics and sharp thresholds

In this manuscript, we study the learning of deep attention neural networks, defined as the composition of multiple self-attention layers, with tied and low-rank weights. We first establish a mapping of such models to sequence multi-index models, a generalization of the widely studied multi-index model to sequential covariates, for which we establish a number of general results. In the context of Bayesian-optimal learning, in the limit of large dimension $D$ and commensurably large number of samples $N$, we derive a sharp asymptotic characterization of the optimal performance as well as the performance of the best-known polynomial-time algorithm for this setting --namely approximate message-passing--, and characterize sharp thresholds on the minimal sample complexity required for better-than-random prediction performance. Our analysis uncovers, in particular, how the different layers are learned sequentially. Finally, we discuss how this sequential learning can also be observed in a realistic setup.

Bilinear Sequence Regression: A Model for Learning from Long Sequences of High-dimensional Tokens

Current progress in artificial intelligence is centered around so-called large language models that consist of neural networks processing long sequences of high-dimensional vectors called tokens. Statistical physics provides powerful tools to study the functioning of learning with neural networks and has played a recognized role in the development of modern machine learning. The statistical physics approach relies on simplified and analytically tractable models of data. However, simple tractable models for long sequences of high-dimensional tokens are largely underexplored. Inspired by the crucial role models such as the single-layer teacher-student perceptron (aka generalized linear regression) played in the theory of fully connected neural networks, in this paper, we introduce and study the bilinear sequence regression (BSR) as one of the most basic models for sequences of tokens. We note that modern architectures naturally subsume the BSR model due to the skip connections. Building on recent methodological progress, we compute the Bayes-optimal generalization error for the model in the limit of long sequences of high-dimensional tokens, and provide a message-passing algorithm that matches this performance. We quantify the improvement that optimal learning brings with respect to vectorizing the sequence of tokens and learning via simple linear regression. We also unveil surprising properties of the gradient descent algorithms in the BSR model.

Building Conformal Prediction Intervals with Approximate Message Passing

Conformal prediction has emerged as a powerful tool for building prediction intervals that are valid in a distribution-free way. However, its evaluation may be computationally costly, especially in the high-dimensional setting where the dimensionality and sample sizes are both large and of comparable magnitudes. To address this challenge in the context of generalized linear regression, we propose a novel algorithm based on Approximate Message Passing (AMP) to accelerate the computation of prediction intervals using full conformal prediction, by approximating the computation of conformity scores. Our work bridges a gap between modern uncertainty quantification techniques and tools for high-dimensional problems involving the AMP algorithm. We evaluate our method on both synthetic and real data, and show that it produces prediction intervals that are close to the baseline methods, while being orders of magnitude faster. Additionally, in the high-dimensional limit and under assumptions on the data distribution, the conformity scores computed by AMP converge to the one computed exactly, which allows theoretical study and benchmarking of conformal methods in high dimensions.

Could ChatGPT get an Engineering Degree? Evaluating Higher Education Vulnerability to AI Assistants

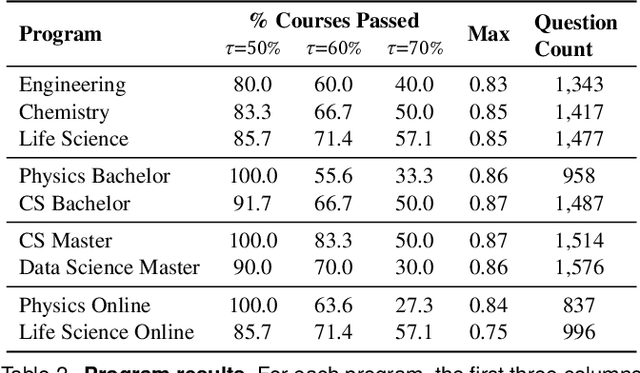
AI assistants are being increasingly used by students enrolled in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level STEM courses. Specifically, we compile a novel dataset of textual assessment questions from 50 courses at EPFL and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass non-project assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.