Could ChatGPT get an Engineering Degree? Evaluating Higher Education Vulnerability to AI Assistants

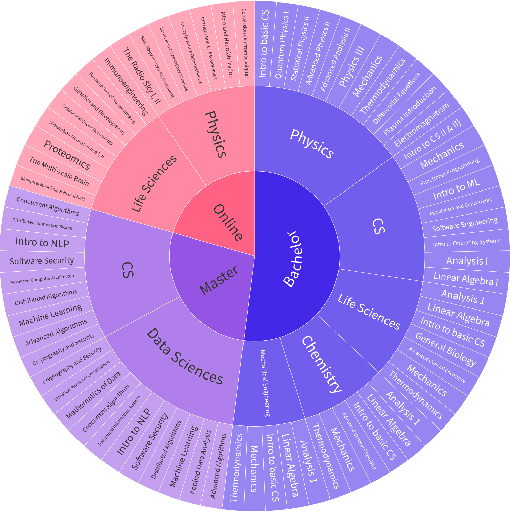
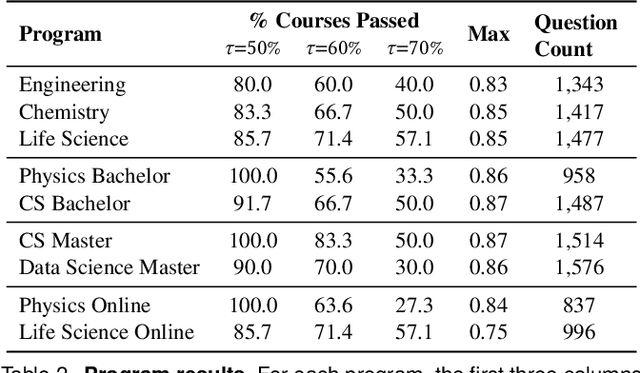
AI assistants are being increasingly used by students enrolled in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level STEM courses. Specifically, we compile a novel dataset of textual assessment questions from 50 courses at EPFL and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass non-project assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.

Understanding Counting in Small Transformers: The Interplay between Attention and Feed-Forward Layers

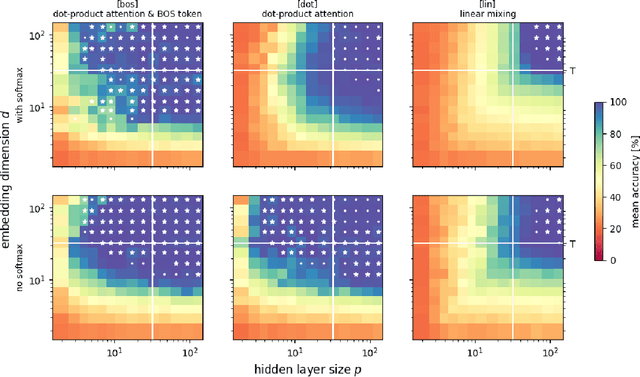
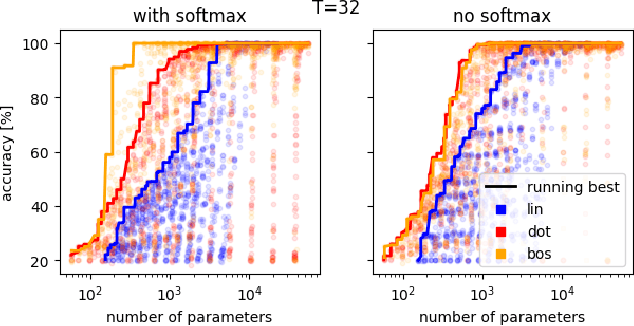
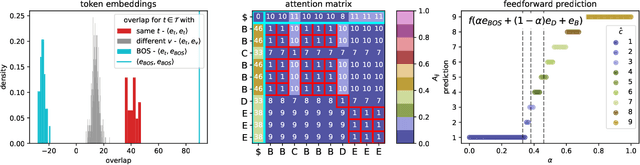
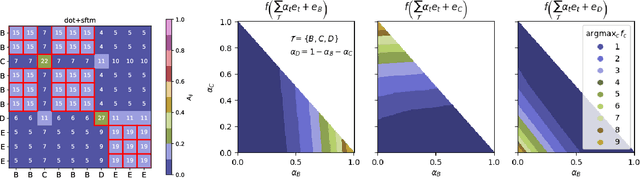
We provide a comprehensive analysis of simple transformer models trained on the histogram task, where the goal is to count the occurrences of each item in the input sequence from a fixed alphabet. Despite its apparent simplicity, this task exhibits a rich phenomenology that allows us to characterize how different architectural components contribute towards the emergence of distinct algorithmic solutions. In particular, we showcase the existence of two qualitatively different mechanisms that implement a solution, relation- and inventory-based counting. Which solution a model can implement depends non-trivially on the precise choice of the attention mechanism, activation function, memorization capacity and the presence of a beginning-of-sequence token. By introspecting learned models on the counting task, we find evidence for the formation of both mechanisms. From a broader perspective, our analysis offers a framework to understand how the interaction of different architectural components of transformer models shapes diverse algorithmic solutions and approximations.

A phase transition between positional and semantic learning in a solvable model of dot-product attention

We investigate how a dot-product attention layer learns a positional attention matrix (with tokens attending to each other based on their respective positions) and a semantic attention matrix (with tokens attending to each other based on their meaning). For an algorithmic task, we experimentally show how the same simple architecture can learn to implement a solution using either the positional or semantic mechanism. On the theoretical side, we study the learning of a non-linear self-attention layer with trainable tied and low-rank query and key matrices. In the asymptotic limit of high-dimensional data and a comparably large number of training samples, we provide a closed-form characterization of the global minimum of the non-convex empirical loss landscape. We show that this minimum corresponds to either a positional or a semantic mechanism and evidence an emergent phase transition from the former to the latter with increasing sample complexity. Finally, we compare the dot-product attention layer to linear positional baseline, and show that it outperforms the latter using the semantic mechanism provided it has access to sufficient data.

Unveiling the Hessian's Connection to the Decision Boundary

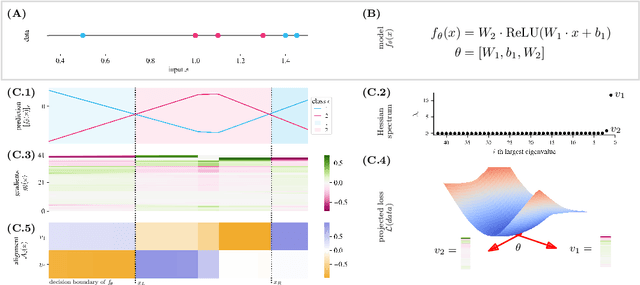
Understanding the properties of well-generalizing minima is at the heart of deep learning research. On the one hand, the generalization of neural networks has been connected to the decision boundary complexity, which is hard to study in the high-dimensional input space. Conversely, the flatness of a minimum has become a controversial proxy for generalization. In this work, we provide the missing link between the two approaches and show that the Hessian top eigenvectors characterize the decision boundary learned by the neural network. Notably, the number of outliers in the Hessian spectrum is proportional to the complexity of the decision boundary. Based on this finding, we provide a new and straightforward approach to studying the complexity of a high-dimensional decision boundary; show that this connection naturally inspires a new generalization measure; and finally, we develop a novel margin estimation technique which, in combination with the generalization measure, precisely identifies minima with simple wide-margin boundaries. Overall, this analysis establishes the connection between the Hessian and the decision boundary and provides a new method to identify minima with simple wide-margin decision boundaries.

Bandits for Learning to Explain from Explanations

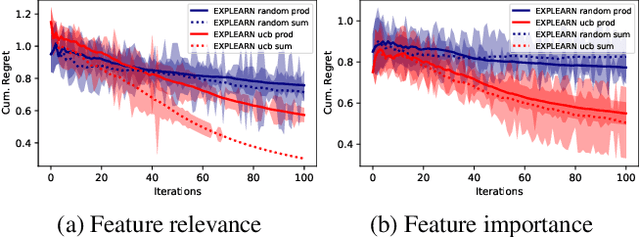
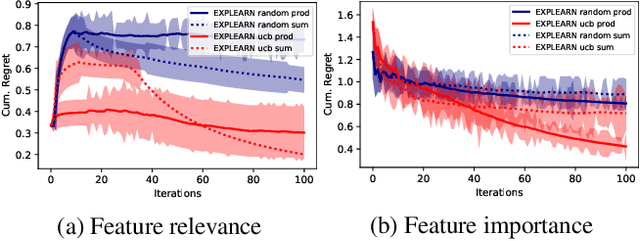
We introduce Explearn, an online algorithm that learns to jointly output predictions and explanations for those predictions. Explearn leverages Gaussian Processes (GP)-based contextual bandits. This brings two key benefits. First, GPs naturally capture different kinds of explanations and enable the system designer to control how explanations generalize across the space by virtue of choosing a suitable kernel. Second, Explearn builds on recent results in contextual bandits which guarantee convergence with high probability. Our initial experiments hint at the promise of the approach.

Neurally Augmented ALISTA

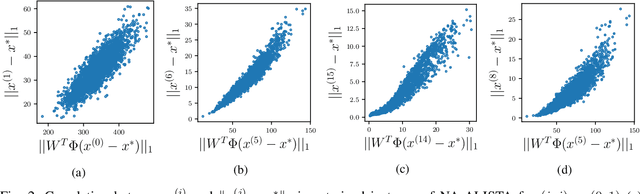
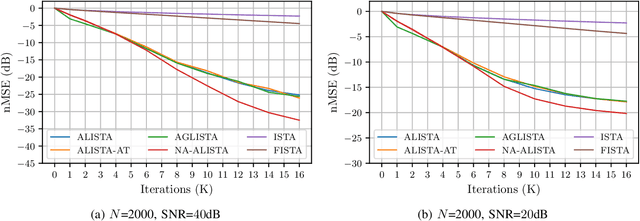
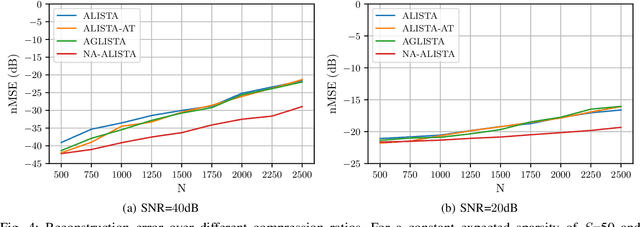
It is well-established that many iterative sparse reconstruction algorithms can be unrolled to yield a learnable neural network for improved empirical performance. A prime example is learned ISTA (LISTA) where weights, step sizes and thresholds are learned from training data. Recently, Analytic LISTA (ALISTA) has been introduced, combining the strong empirical performance of a fully learned approach like LISTA, while retaining theoretical guarantees of classical compressed sensing algorithms and significantly reducing the number of parameters to learn. However, these parameters are trained to work in expectation, often leading to suboptimal reconstruction of individual targets. In this work we therefore introduce Neurally Augmented ALISTA, in which an LSTM network is used to compute step sizes and thresholds individually for each target vector during reconstruction. This adaptive approach is theoretically motivated by revisiting the recovery guarantees of ALISTA. We show that our approach further improves empirical performance in sparse reconstruction, in particular outperforming existing algorithms by an increasing margin as the compression ratio becomes more challenging.