A Random Matrix Theory Perspective on the Spectrum of Learned Features and Asymptotic Generalization Capabilities

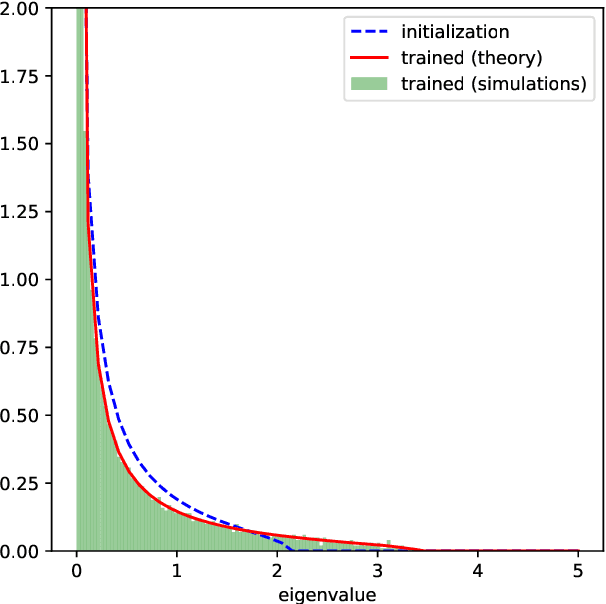
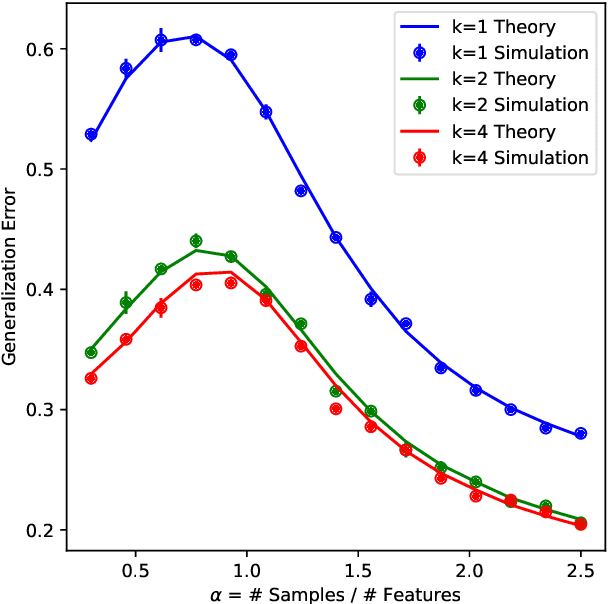
A key property of neural networks is their capacity of adapting to data during training. Yet, our current mathematical understanding of feature learning and its relationship to generalization remain limited. In this work, we provide a random matrix analysis of how fully-connected two-layer neural networks adapt to the target function after a single, but aggressive, gradient descent step. We rigorously establish the equivalence between the updated features and an isotropic spiked random feature model, in the limit of large batch size. For the latter model, we derive a deterministic equivalent description of the feature empirical covariance matrix in terms of certain low-dimensional operators. This allows us to sharply characterize the impact of training in the asymptotic feature spectrum, and in particular, provides a theoretical grounding for how the tails of the feature spectrum modify with training. The deterministic equivalent further yields the exact asymptotic generalization error, shedding light on the mechanisms behind its improvement in the presence of feature learning. Our result goes beyond standard random matrix ensembles, and therefore we believe it is of independent technical interest. Different from previous work, our result holds in the challenging maximal learning rate regime, is fully rigorous and allows for finitely supported second layer initialization, which turns out to be crucial for studying the functional expressivity of the learned features. This provides a sharp description of the impact of feature learning in the generalization of two-layer neural networks, beyond the random features and lazy training regimes.

High-dimensional learning of narrow neural networks

Recent years have been marked with the fast-pace diversification and increasing ubiquity of machine learning applications. Yet, a firm theoretical understanding of the surprising efficiency of neural networks to learn from high-dimensional data still proves largely elusive. In this endeavour, analyses inspired by statistical physics have proven instrumental, enabling the tight asymptotic characterization of the learning of neural networks in high dimensions, for a broad class of solvable models. This manuscript reviews the tools and ideas underlying recent progress in this line of work. We introduce a generic model -- the sequence multi-index model -- which encompasses numerous previously studied models as special instances. This unified framework covers a broad class of machine learning architectures with a finite number of hidden units, including multi-layer perceptrons, autoencoders, attention mechanisms; and tasks, including (un)supervised learning, denoising, contrastive learning, in the limit of large data dimension, and comparably large number of samples. We explicate in full detail the analysis of the learning of sequence multi-index models, using statistical physics techniques such as the replica method and approximate message-passing algorithms. This manuscript thus provides a unified presentation of analyses reported in several previous works, and a detailed overview of central techniques in the field of statistical physics of machine learning. This review should be a useful primer for machine learning theoreticians curious of statistical physics approaches; it should also be of value to statistical physicists interested in the transfer of such ideas to the study of neural networks.

Asymptotics of Learning with Deep Structured (Random) Features

For a large class of feature maps we provide a tight asymptotic characterisation of the test error associated with learning the readout layer, in the high-dimensional limit where the input dimension, hidden layer widths, and number of training samples are proportionally large. This characterization is formulated in terms of the population covariance of the features. Our work is partially motivated by the problem of learning with Gaussian rainbow neural networks, namely deep non-linear fully-connected networks with random but structured weights, whose row-wise covariances are further allowed to depend on the weights of previous layers. For such networks we also derive a closed-form formula for the feature covariance in terms of the weight matrices. We further find that in some cases our results can capture feature maps learned by deep, finite-width neural networks trained under gradient descent.

Asymptotics of feature learning in two-layer networks after one gradient-step

In this manuscript we investigate the problem of how two-layer neural networks learn features from data, and improve over the kernel regime, after being trained with a single gradient descent step. Leveraging a connection from (Ba et al., 2022) with a non-linear spiked matrix model and recent progress on Gaussian universality (Dandi et al., 2023), we provide an exact asymptotic description of the generalization error in the high-dimensional limit where the number of samples $n$, the width $p$ and the input dimension $d$ grow at a proportional rate. We characterize exactly how adapting to the data is crucial for the network to efficiently learn non-linear functions in the direction of the gradient -- where at initialization it can only express linear functions in this regime. To our knowledge, our results provides the first tight description of the impact of feature learning in the generalization of two-layer neural networks in the large learning rate regime $\eta=\Theta_{d}(d)$, beyond perturbative finite width corrections of the conjugate and neural tangent kernels.

A phase transition between positional and semantic learning in a solvable model of dot-product attention

We investigate how a dot-product attention layer learns a positional attention matrix (with tokens attending to each other based on their respective positions) and a semantic attention matrix (with tokens attending to each other based on their meaning). For an algorithmic task, we experimentally show how the same simple architecture can learn to implement a solution using either the positional or semantic mechanism. On the theoretical side, we study the learning of a non-linear self-attention layer with trainable tied and low-rank query and key matrices. In the asymptotic limit of high-dimensional data and a comparably large number of training samples, we provide a closed-form characterization of the global minimum of the non-convex empirical loss landscape. We show that this minimum corresponds to either a positional or a semantic mechanism and evidence an emergent phase transition from the former to the latter with increasing sample complexity. Finally, we compare the dot-product attention layer to linear positional baseline, and show that it outperforms the latter using the semantic mechanism provided it has access to sufficient data.

Analysis of learning a flow-based generative model from limited sample complexity

We study the problem of training a flow-based generative model, parametrized by a two-layer autoencoder, to sample from a high-dimensional Gaussian mixture. We provide a sharp end-to-end analysis of the problem. First, we provide a tight closed-form characterization of the learnt velocity field, when parametrized by a shallow denoising auto-encoder trained on a finite number $n$ of samples from the target distribution. Building on this analysis, we provide a sharp description of the corresponding generative flow, which pushes the base Gaussian density forward to an approximation of the target density. In particular, we provide closed-form formulae for the distance between the mean of the generated mixture and the mean of the target mixture, which we show decays as $\Theta_n(\frac{1}{n})$. Finally, this rate is shown to be in fact Bayes-optimal.

High-dimensional Asymptotics of Denoising Autoencoders

We address the problem of denoising data from a Gaussian mixture using a two-layer non-linear autoencoder with tied weights and a skip connection. We consider the high-dimensional limit where the number of training samples and the input dimension jointly tend to infinity while the number of hidden units remains bounded. We provide closed-form expressions for the denoising mean-squared test error. Building on this result, we quantitatively characterize the advantage of the considered architecture over the autoencoder without the skip connection that relates closely to principal component analysis. We further show that our results accurately capture the learning curves on a range of real data sets.

Optimal Learning of Deep Random Networks of Extensive-width

We consider the problem of learning a target function corresponding to a deep, extensive-width, non-linear neural network with random Gaussian weights. We consider the asymptotic limit where the number of samples, the input dimension and the network width are proportionally large. We derive a closed-form expression for the Bayes-optimal test error, for regression and classification tasks. We contrast these Bayes-optimal errors with the test errors of ridge regression, kernel and random features regression. We find, in particular, that optimally regularized ridge regression, as well as kernel regression, achieve Bayes-optimal performances, while the logistic loss yields a near-optimal test error for classification. We further show numerically that when the number of samples grows faster than the dimension, ridge and kernel methods become suboptimal, while neural networks achieve test error close to zero from quadratically many samples.

Deterministic equivalent and error universality of deep random features learning

This manuscript considers the problem of learning a random Gaussian network function using a fully connected network with frozen intermediate layers and trainable readout layer. This problem can be seen as a natural generalization of the widely studied random features model to deeper architectures. First, we prove Gaussian universality of the test error in a ridge regression setting where the learner and target networks share the same intermediate layers, and provide a sharp asymptotic formula for it. Establishing this result requires proving a deterministic equivalent for traces of the deep random features sample covariance matrices which can be of independent interest. Second, we conjecture the asymptotic Gaussian universality of the test error in the more general setting of arbitrary convex losses and generic learner/target architectures. We provide extensive numerical evidence for this conjecture, which requires the derivation of closed-form expressions for the layer-wise post-activation population covariances. In light of our results, we investigate the interplay between architecture design and implicit regularization.

Error Rates for Kernel Classification under Source and Capacity Conditions

In this manuscript, we consider the problem of kernel classification under the Gaussian data design, and under source and capacity assumptions on the dataset. While the decay rates of the prediction error have been extensively studied under much more generic assumptions for kernel ridge regression, deriving decay rates for the classification problem has been hitherto considered a much more challenging task. In this work we leverage recent analytical results for learning curves of linear classification with generic loss function to derive the rates of decay of the misclassification (prediction) error with the sample complexity for two standard classification settings, namely margin-maximizing Support Vector Machines (SVM) and ridge classification. Using numerical and analytical arguments, we derive the error rates as a function of the source and capacity coefficients, and contrast the two methods.