MGD: Moment Guided Diffusion for Maximum Entropy Generation

Generating samples from limited information is a fundamental problem across scientific domains. Classical maximum entropy methods provide principled uncertainty quantification from moment constraints but require sampling via MCMC or Langevin dynamics, which typically exhibit exponential slowdown in high dimensions. In contrast, generative models based on diffusion and flow matching efficiently transport noise to data but offer limited theoretical guarantees and can overfit when data is scarce. We introduce Moment Guided Diffusion (MGD), which combines elements of both approaches. Building on the stochastic interpolant framework, MGD samples maximum entropy distributions by solving a stochastic differential equation that guides moments toward prescribed values in finite time, thereby avoiding slow mixing in equilibrium-based methods. We formally obtain, in the large-volatility limit, convergence of MGD to the maximum entropy distribution and derive a tractable estimator of the resulting entropy computed directly from the dynamics. Applications to financial time series, turbulent flows, and cosmological fields using wavelet scattering moments yield estimates of negentropy for high-dimensional multiscale processes.

Variational Optimality of Föllmer Processes in Generative Diffusions

We construct and analyze generative diffusions that transport a point mass to a prescribed target distribution over a finite time horizon using the stochastic interpolant framework. The drift is expressed as a conditional expectation that can be estimated from independent samples without simulating stochastic processes. We show that the diffusion coefficient can be tuned \emph{a~posteriori} without changing the time-marginal distributions. Among all such tunings, we prove that minimizing the impact of estimation error on the path-space Kullback--Leibler divergence selects, in closed form, a Föllmer process -- a diffusion whose path measure minimizes relative entropy with respect to a reference process determined by the interpolation schedules alone. This yields a new variational characterization of Föllmer processes, complementing classical formulations via Schrödinger bridges and stochastic control. We further establish that, under this optimal diffusion coefficient, the path-space Kullback--Leibler divergence becomes independent of the interpolation schedule, rendering different schedules statistically equivalent in this variational sense.

Generative Modeling from Black-box Corruptions via Self-Consistent Stochastic Interpolants

Transport-based methods have emerged as a leading paradigm for building generative models from large, clean datasets. However, in many scientific and engineering domains, clean data are often unavailable: instead, we only observe measurements corrupted through a noisy, ill-conditioned channel. A generative model for the original data thus requires solving an inverse problem at the level of distributions. In this work, we introduce a novel approach to this task based on Stochastic Interpolants: we iteratively update a transport map between corrupted and clean data samples using only access to the corrupted dataset as well as black box access to the corruption channel. Under appropriate conditions, this iterative procedure converges towards a self-consistent transport map that effectively inverts the corruption channel, thus enabling a generative model for the clean data. We refer to the resulting method as the self-consistent stochastic interpolant (SCSI). It (i) is computationally efficient compared to variational alternatives, (ii) highly flexible, handling arbitrary nonlinear forward models with only black-box access, and (iii) enjoys theoretical guarantees. We demonstrate superior performance on inverse problems in natural image processing and scientific reconstruction, and establish convergence guarantees of the scheme under appropriate assumptions.

Multitask Learning with Stochastic Interpolants

We propose a framework for learning maps between probability distributions that broadly generalizes the time dynamics of flow and diffusion models. To enable this, we generalize stochastic interpolants by replacing the scalar time variable with vectors, matrices, or linear operators, allowing us to bridge probability distributions across multiple dimensional spaces. This approach enables the construction of versatile generative models capable of fulfilling multiple tasks without task-specific training. Our operator-based interpolants not only provide a unifying theoretical perspective for existing generative models but also extend their capabilities. Through numerical experiments, we demonstrate the zero-shot efficacy of our method on conditional generation and inpainting, fine-tuning and posterior sampling, and multiscale modeling, suggesting its potential as a generic task-agnostic alternative to specialized models.

How to build a consistency model: Learning flow maps via self-distillation

Building on the framework proposed in Boffi et al. (2024), we present a systematic approach for learning flow maps associated with flow and diffusion models. Flow map-based models, commonly known as consistency models, encompass recent efforts to improve the efficiency of generative models based on solutions to differential equations. By exploiting a relationship between the velocity field underlying a continuous-time flow and the instantaneous rate of change of the flow map, we show how to convert existing distillation schemes into direct training algorithms via self-distillation, eliminating the need for pre-trained models. We empirically evaluate several instantiations of our framework, finding that high-dimensional tasks like image synthesis benefit from objective functions that avoid temporal and spatial derivatives of the flow map, while lower-dimensional tasks can benefit from objectives incorporating higher-order derivatives to capture sharp features.

FEAT: Free energy Estimators with Adaptive Transport

We present Free energy Estimators with Adaptive Transport (FEAT), a novel framework for free energy estimation -- a critical challenge across scientific domains. FEAT leverages learned transports implemented via stochastic interpolants and provides consistent, minimum-variance estimators based on escorted Jarzynski equality and controlled Crooks theorem, alongside variational upper and lower bounds on free energy differences. Unifying equilibrium and non-equilibrium methods under a single theoretical framework, FEAT establishes a principled foundation for neural free energy calculations. Experimental validation on toy examples, molecular simulations, and quantum field theory demonstrates improvements over existing learning-based methods.

Optimizing Noise Schedules of Generative Models in High Dimensionss

Recent works have shown that diffusion models can undergo phase transitions, the resolution of which is needed for accurately generating samples. This has motivated the use of different noise schedules, the two most common choices being referred to as variance preserving (VP) and variance exploding (VE). Here we revisit these schedules within the framework of stochastic interpolants. Using the Gaussian Mixture (GM) and Curie-Weiss (CW) data distributions as test case models, we first investigate the effect of the variance of the initial noise distribution and show that VP recovers the low-level feature (the distribution of each mode) but misses the high-level feature (the asymmetry between modes), whereas VE performs oppositely. We also show that this dichotomy, which happens when denoising by a constant amount in each step, can be avoided by using noise schedules specific to VP and VE that allow for the recovery of both high- and low-level features. Finally we show that these schedules yield generative models for the GM and CW model whose probability flow ODE can be discretized using $\Theta_d(1)$ steps in dimension $d$ instead of the $\Theta_d(\sqrt{d})$ steps required by constant denoising.

Model-free learning of probability flows: Elucidating the nonequilibrium dynamics of flocking

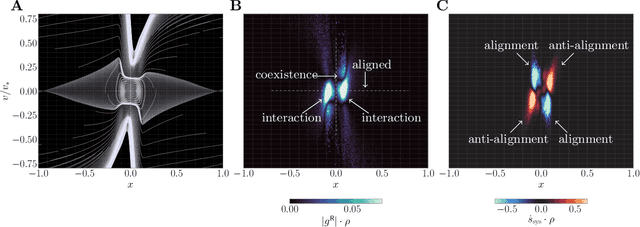
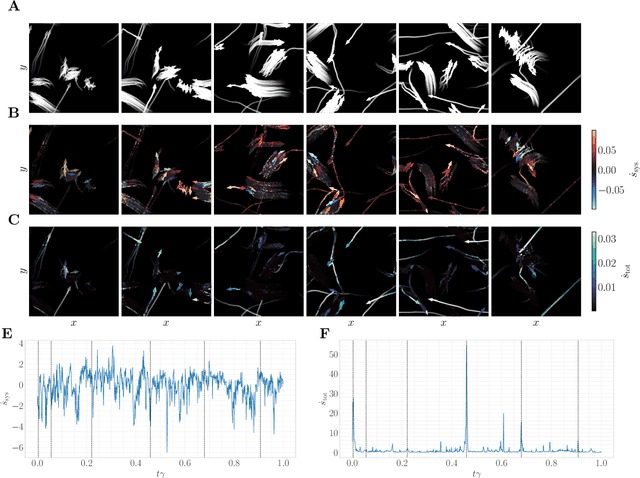
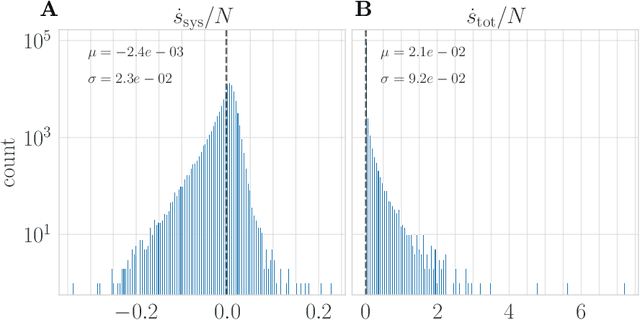
Active systems comprise a class of nonequilibrium dynamics in which individual components autonomously dissipate energy. Efforts towards understanding the role played by activity have centered on computation of the entropy production rate (EPR), which quantifies the breakdown of time reversal symmetry. A fundamental difficulty in this program is that high dimensionality of the phase space renders traditional computational techniques infeasible for estimating the EPR. Here, we overcome this challenge with a novel deep learning approach that estimates probability currents directly from stochastic system trajectories. We derive a new physical connection between the probability current and two local definitions of the EPR for inertial systems, which we apply to characterize the departure from equilibrium in a canonical model of flocking. Our results highlight that entropy is produced and consumed on the spatial interface of a flock as the interplay between alignment and fluctuation dynamically creates and annihilates order. By enabling the direct visualization of when and where a given system is out of equilibrium, we anticipate that our methodology will advance the understanding of a broad class of complex nonequilibrium dynamics.

A Simulation-Free Deep Learning Approach to Stochastic Optimal Control

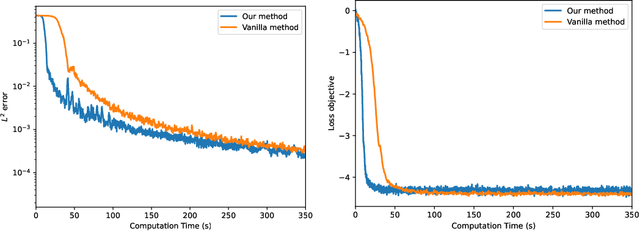
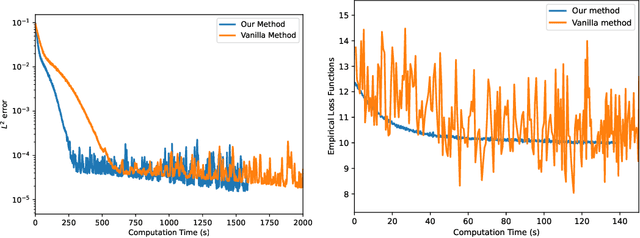
We propose a simulation-free algorithm for the solution of generic problems in stochastic optimal control (SOC). Unlike existing methods, our approach does not require the solution of an adjoint problem, but rather leverages Girsanov theorem to directly calculate the gradient of the SOC objective on-policy. This allows us to speed up the optimization of control policies parameterized by neural networks since it completely avoids the expensive back-propagation step through stochastic differential equations (SDEs) used in the Neural SDE framework. In particular, it enables us to solve SOC problems in high dimension and on long time horizons. We demonstrate the efficiency of our approach in various domains of applications, including standard stochastic optimal control problems, sampling from unnormalized distributions via construction of a Schr\"odinger-F\"ollmer process, and fine-tuning of pre-trained diffusion models. In all cases our method is shown to outperform the existing methods in both the computing time and memory efficiency.

NETS: A Non-Equilibrium Transport Sampler

We propose an algorithm, termed the Non-Equilibrium Transport Sampler (NETS), to sample from unnormalized probability distributions. NETS can be viewed as a variant of annealed importance sampling (AIS) based on Jarzynski's equality, in which the stochastic differential equation used to perform the non-equilibrium sampling is augmented with an additional learned drift term that lowers the impact of the unbiasing weights used in AIS. We show that this drift is the minimizer of a variety of objective functions, which can all be estimated in an unbiased fashion without backpropagating through solutions of the stochastic differential equations governing the sampling. We also prove that some these objectives control the Kullback-Leibler divergence of the estimated distribution from its target. NETS is shown to be unbiased and, in addition, has a tunable diffusion coefficient which can be adjusted post-training to maximize the effective sample size. We demonstrate the efficacy of the method on standard benchmarks, high-dimensional Gaussian mixture distributions, and a model from statistical lattice field theory, for which it surpasses the performances of related work and existing baselines.